2023-2024学年人教版九年级数学上册22.3实际问题与二次函数 同步练习 (含答案)
文档属性
| 名称 | 2023-2024学年人教版九年级数学上册22.3实际问题与二次函数 同步练习 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 836.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 00:00:00 | ||
图片预览


文档简介
22.3实际问题与二次函数同步练习
一、单选题
1.据省统计局公布的数据,合肥市2021年第一季度总值约为2.4千亿元人民币,若我市第三季度总值为千亿元人民币,平均每个季度增长的百分率为,则关于的函数表达式是( )
A. B.
C. D.
2.洗手盘台面上有一瓶洗手液.当同学用一定的力按住顶部下压如图位置时,洗手液从喷口流出,路线近似呈抛物线状,且喷口为该抛物线的顶点.洗手液瓶子的截面图下面部分是矩形.同学测得:洗手液瓶子的底面直径,喷嘴位置点距台面的距离为,且、、三点共线.在距离台面处接洗手液时,手心到直线的水平距离为,不去接则洗手液落在台面的位置距的水平面是( )
A. B. C. D.
3.已知实心球运动的高度与水平距离之间的函数关系是,则该同学此次投掷实心球的成绩是( )
A. B. C. D.
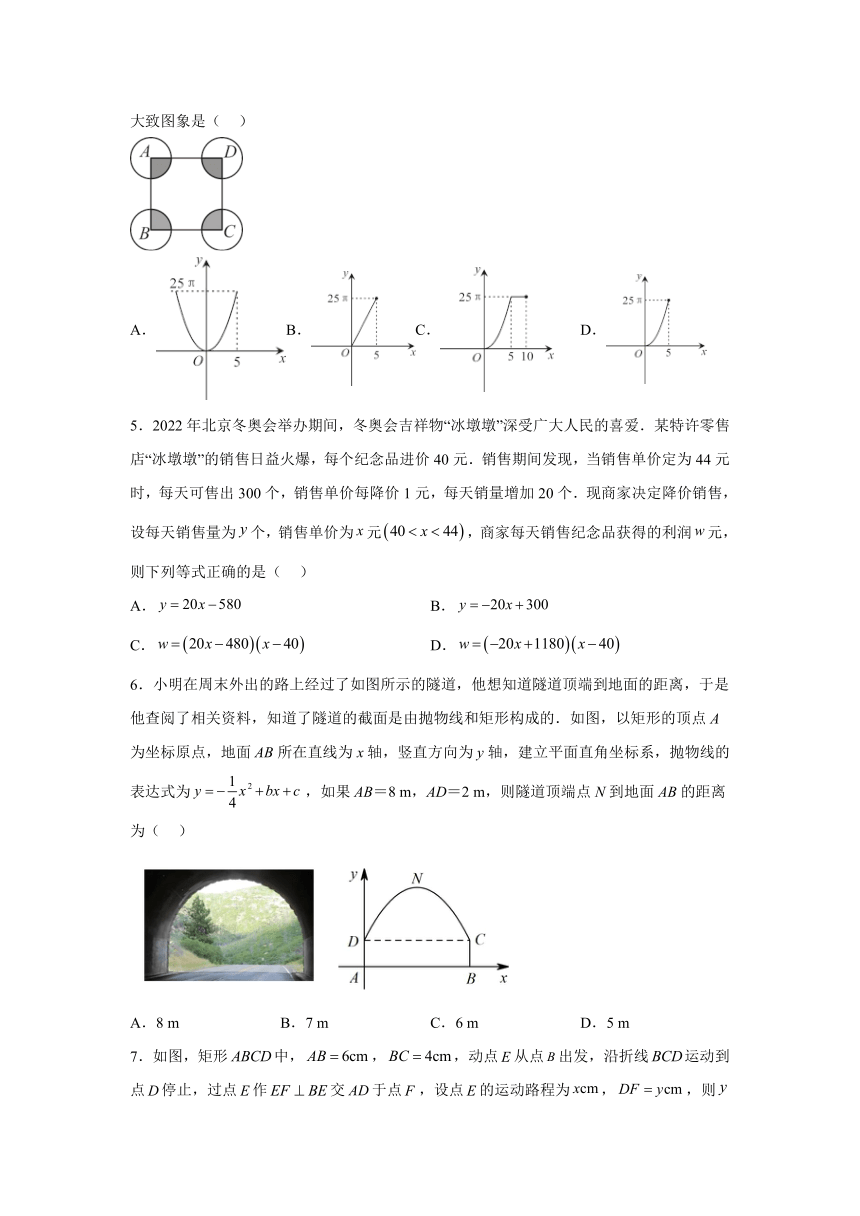
4.如图,正方形的边长为,以正方形的顶点A、、、为圆心画四个全等的圆,若圆的半径为,且,阴影部分的面积为,则能反映与之间函数关系的大致图象是( )
A.B.C. D.
5.2022年北京冬奥会举办期间,冬奥会吉祥物“冰墩墩”深受广大人民的喜爱.某特许零售店“冰墩墩”的销售日益火爆,每个纪念品进价40元.销售期间发现,当销售单价定为44元时,每天可售出300个,销售单价每降价1元,每天销量增加20个.现商家决定降价销售,设每天销售量为个,销售单价为元,商家每天销售纪念品获得的利润元,则下列等式正确的是( )
A. B.
C. D.
6.小明在周末外出的路上经过了如图所示的隧道,他想知道隧道顶端到地面的距离,于是他查阅了相关资料,知道了隧道的截面是由抛物线和矩形构成的.如图,以矩形的顶点A为坐标原点,地面AB所在直线为x轴,竖直方向为y轴,建立平面直角坐标系,抛物线的表达式为,如果AB=8 m,AD=2 m,则隧道顶端点N到地面AB的距离为( )
A.8 m B.7 m C.6 m D.5 m
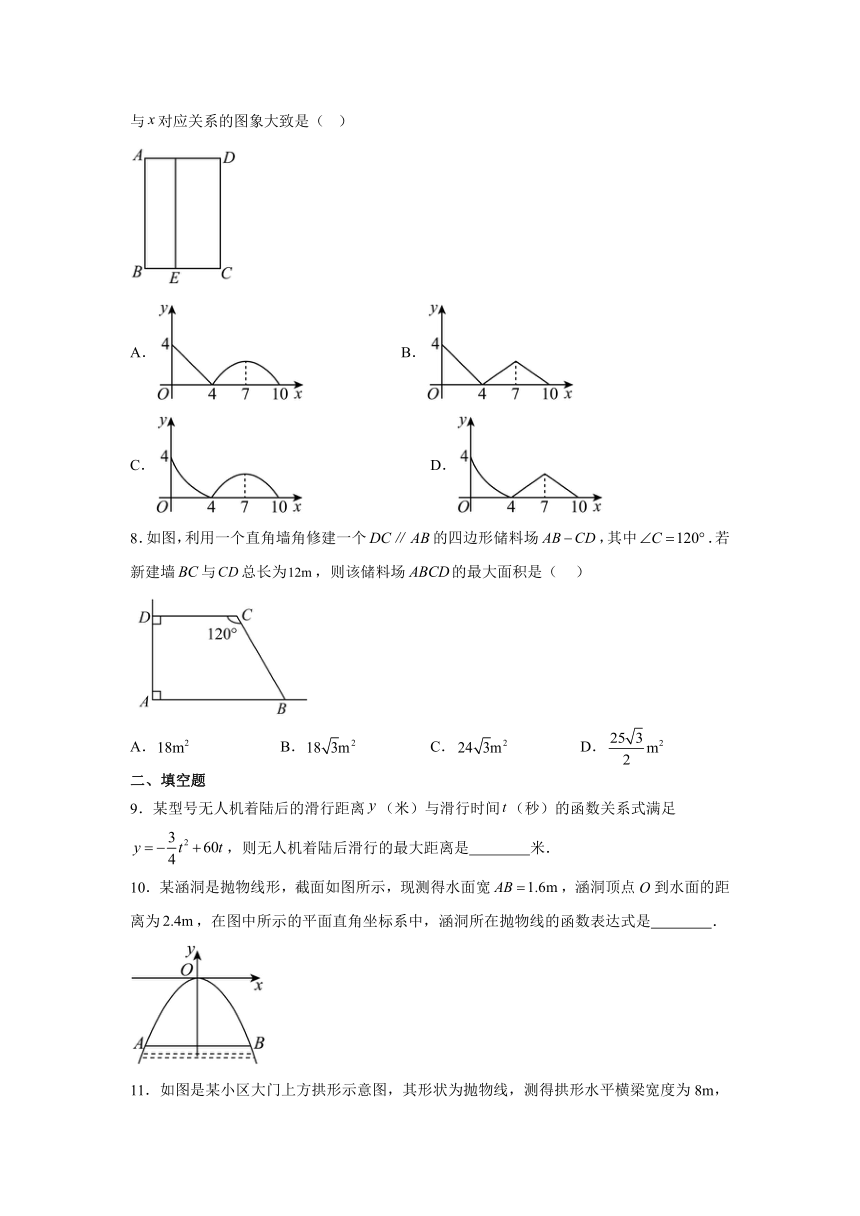
7.如图,矩形中,,,动点从点出发,沿折线运动到点停止,过点作交于点,设点的运动路程为,,则与对应关系的图象大致是( )
A. B.
C. D.
8.如图,利用一个直角墙角修建一个的四边形储料场,其中.若新建墙与总长为,则该储料场的最大面积是( )
A. B. C. D.
二、填空题
9.某型号无人机着陆后的滑行距离(米)与滑行时间(秒)的函数关系式满足,则无人机着陆后滑行的最大距离是 米.
10.某涵洞是抛物线形,截面如图所示,现测得水面宽,涵洞顶点O到水面的距离为,在图中所示的平面直角坐标系中,涵洞所在抛物线的函数表达式是 .
11.如图是某小区大门上方拱形示意图,其形状为抛物线,测得拱形水平横梁宽度为8m,拱高为2m,在五一节到来之际,拟在该拱形上悬挂灯笼(高度为1m),要求相邻两盏灯笼的水平间距均为1m,挂满后不擦横梁且成轴对称分布,则最多可以悬挂 个灯笼.
12.某超市销售一种饮料,每瓶进价为9元.经市场调查表明,当售价在10元到14元之间(含10元,14元)浮动时,日均销售量(瓶)与每瓶销售价(元)之间满足函数关系式.当销售价格定为每瓶 元时,所得日均毛利润最大(每瓶毛利润=每瓶售价-每瓶进价).
13.如图,二次函数与x轴交于点A,B,对称轴为直线l,顶点C到x轴的距离为.点P为直线l上一动点,另一点从C出发,先以每秒2个单位长度的速度沿运动到点P,再以每秒1个单位长度的速度沿运动到点A停止,则时间最短为 秒.
三、解答题
14.如图1,小兵和小伙伴一起玩扔小石头游戏,我们把小石头的运动轨迹看成是抛物线的一部分.如图所示,以点为原点建立平面直角坐标系.已知扔小石头的出手点在点正上方米的位置,小石头在与点的水平距离为米时达到最高高度米;为扔小石头的预期击中目标,点在轴上,离点的水平距离为米,点在点的正上方米.
(1)小兵扔的小石头能否正好击中点,并说明理由;
(2)求小石头运动轨迹所在抛物线的解析式;
(3)求出小石头在运动过程中与直线的最大竖直距离.
15.为了打造“清洁能源示范城市”,东营市2016年投入资金2560万元用于充电桩的安装,并规划投入资金逐年增加,2018年在2016年的基础上增加投入资金3200万元.
(1)从2016年到2018年,东营市用于充电桩安装的资金年平均增长率为多少?
(2)2019年东营市计划再安装A、B两种型号的充电桩共200个.已知安装一个A型充电桩需3.5万元,安装一个B型充电桩需4万元,且A型充电桩的数量不多于B型充电桩的一半.求A、B两种型号充电桩各安装多少个时,所需资金最少,最少为多少?
16.如图,某市民政局欲给敬老院修建一个半径为米的圆形喷水池,在池中心竖直安装一根水管,在水管的顶端点处安一个喷水头,测得喷水头距地面的高度为,水柱在距喷水头水平距离处达到最高,建立如图所示的平面直角坐标系,并设抛物线的表达式为,其中是水柱距喷水头的水平距离,是水柱距地面的高度.
(1)求抛物线的表达式;
(2)请你通过计算说明喷出的水柱是否会落到圆形喷水池的外面.
17.姣姣进行铅球专业训练,教练员尝试用数学模型来研究铅球的运动情况,从而做出指导.如图是姣姣在某次比赛前训练时,铅球行进高度与水平距离之间的函数图象,铅球经过的路径可以看作抛物线.铅球在距离地面的A处出手,在距离出手点A水平距离处(即)达到最高点,这次训练的成绩是.
(1)求这次训练中铅球经过路径的函数表达式;
(2)求这次训练中,铅球距离地面的最大高度为多少;
(3)这次训练中,铅球抛出的水平距离多大时,铅球离地面的高度为?
参考答案
1--8CDBDD CAC
9.
10.
11.6
12.13
13.
14.(1)解:小兵扔的小石头能击中点,理由如下:
根据题意,可得:抛物线的对称轴为,
又根据题意,可得:,,
点和点关于对称,
点在抛物线上,
小兵扔的小石头能击中点;
(2)解:根据题意,可得:抛物线的顶点坐标为,
设抛物线的解析式为,
又点经过抛物线,
把的坐标代入解析式,可得:,
解得:,
抛物线的解析式为,
又根据题意,可得:该抛物线的自变量的取值范围为,
小石头运动轨迹所在抛物线的解析式为,
(3)解:如图,连接,设直线的解析式为,
把代入,可得:,
解得:,
直线的解析式为,
设直线上方的抛物线上的一点的坐标为,
过点作轴,交于点,则的坐标为,
,
当时,有最大值,最大值为,
小石头在运动过程中与直线的最大竖直距离为.
15.(1)设从2016年到2018年,东营市用于充电桩安装的资金年平均增长率为x,
根据题意得:,
解得:,(舍去).
答:从2016年到2018年,东营市用于充电桩安装的资金年平均增长率为50%;
(2)设安装A型充电桩a个,则安装B型充电桩个,所需资金为万元.
根据题意,得:,
解得:,
,
∵,
∴随a的增大而减小.
∵a为整数,
∴当时,最小,最小值为(万元).
此时,.
答:A、B两种型号充电桩分别安装66个,134个时,所需资金最少,最少为767万元.
16.(1)由题意可知,抛物线的顶点坐标为,
则,,
抛物线的表达式为,
将代入上式得,,
解得,,
抛物线的表达式为.
(2)当时,,
解得,,舍去,
,
喷出的水柱不会落到圆形喷水池的外面.
17.(1)解:如下如图所示:设经过的路径与地面的交点为D,
依题意得:,,
∵在距离出手点A水平距离处(即)达到最高点,
∴图象的对称轴是直线,即直线
设这次训练中铅球经过路径的函数表达式为:
将点,代入得:
解得:
∴这次训练中铅球经过路径的函数表达式为:
(2)∵,
∴当时,
答:这次训练中,铅球距离地面的最大高度为.
(3)令,
解得:
答:这次训练中,铅球抛出的水平距离或时,铅球离地面的高度为.
一、单选题
1.据省统计局公布的数据,合肥市2021年第一季度总值约为2.4千亿元人民币,若我市第三季度总值为千亿元人民币,平均每个季度增长的百分率为,则关于的函数表达式是( )
A. B.
C. D.
2.洗手盘台面上有一瓶洗手液.当同学用一定的力按住顶部下压如图位置时,洗手液从喷口流出,路线近似呈抛物线状,且喷口为该抛物线的顶点.洗手液瓶子的截面图下面部分是矩形.同学测得:洗手液瓶子的底面直径,喷嘴位置点距台面的距离为,且、、三点共线.在距离台面处接洗手液时,手心到直线的水平距离为,不去接则洗手液落在台面的位置距的水平面是( )
A. B. C. D.
3.已知实心球运动的高度与水平距离之间的函数关系是,则该同学此次投掷实心球的成绩是( )
A. B. C. D.
4.如图,正方形的边长为,以正方形的顶点A、、、为圆心画四个全等的圆,若圆的半径为,且,阴影部分的面积为,则能反映与之间函数关系的大致图象是( )
A.B.C. D.
5.2022年北京冬奥会举办期间,冬奥会吉祥物“冰墩墩”深受广大人民的喜爱.某特许零售店“冰墩墩”的销售日益火爆,每个纪念品进价40元.销售期间发现,当销售单价定为44元时,每天可售出300个,销售单价每降价1元,每天销量增加20个.现商家决定降价销售,设每天销售量为个,销售单价为元,商家每天销售纪念品获得的利润元,则下列等式正确的是( )
A. B.
C. D.
6.小明在周末外出的路上经过了如图所示的隧道,他想知道隧道顶端到地面的距离,于是他查阅了相关资料,知道了隧道的截面是由抛物线和矩形构成的.如图,以矩形的顶点A为坐标原点,地面AB所在直线为x轴,竖直方向为y轴,建立平面直角坐标系,抛物线的表达式为,如果AB=8 m,AD=2 m,则隧道顶端点N到地面AB的距离为( )
A.8 m B.7 m C.6 m D.5 m
7.如图,矩形中,,,动点从点出发,沿折线运动到点停止,过点作交于点,设点的运动路程为,,则与对应关系的图象大致是( )
A. B.
C. D.
8.如图,利用一个直角墙角修建一个的四边形储料场,其中.若新建墙与总长为,则该储料场的最大面积是( )
A. B. C. D.
二、填空题
9.某型号无人机着陆后的滑行距离(米)与滑行时间(秒)的函数关系式满足,则无人机着陆后滑行的最大距离是 米.
10.某涵洞是抛物线形,截面如图所示,现测得水面宽,涵洞顶点O到水面的距离为,在图中所示的平面直角坐标系中,涵洞所在抛物线的函数表达式是 .
11.如图是某小区大门上方拱形示意图,其形状为抛物线,测得拱形水平横梁宽度为8m,拱高为2m,在五一节到来之际,拟在该拱形上悬挂灯笼(高度为1m),要求相邻两盏灯笼的水平间距均为1m,挂满后不擦横梁且成轴对称分布,则最多可以悬挂 个灯笼.
12.某超市销售一种饮料,每瓶进价为9元.经市场调查表明,当售价在10元到14元之间(含10元,14元)浮动时,日均销售量(瓶)与每瓶销售价(元)之间满足函数关系式.当销售价格定为每瓶 元时,所得日均毛利润最大(每瓶毛利润=每瓶售价-每瓶进价).
13.如图,二次函数与x轴交于点A,B,对称轴为直线l,顶点C到x轴的距离为.点P为直线l上一动点,另一点从C出发,先以每秒2个单位长度的速度沿运动到点P,再以每秒1个单位长度的速度沿运动到点A停止,则时间最短为 秒.
三、解答题
14.如图1,小兵和小伙伴一起玩扔小石头游戏,我们把小石头的运动轨迹看成是抛物线的一部分.如图所示,以点为原点建立平面直角坐标系.已知扔小石头的出手点在点正上方米的位置,小石头在与点的水平距离为米时达到最高高度米;为扔小石头的预期击中目标,点在轴上,离点的水平距离为米,点在点的正上方米.
(1)小兵扔的小石头能否正好击中点,并说明理由;
(2)求小石头运动轨迹所在抛物线的解析式;
(3)求出小石头在运动过程中与直线的最大竖直距离.
15.为了打造“清洁能源示范城市”,东营市2016年投入资金2560万元用于充电桩的安装,并规划投入资金逐年增加,2018年在2016年的基础上增加投入资金3200万元.
(1)从2016年到2018年,东营市用于充电桩安装的资金年平均增长率为多少?
(2)2019年东营市计划再安装A、B两种型号的充电桩共200个.已知安装一个A型充电桩需3.5万元,安装一个B型充电桩需4万元,且A型充电桩的数量不多于B型充电桩的一半.求A、B两种型号充电桩各安装多少个时,所需资金最少,最少为多少?
16.如图,某市民政局欲给敬老院修建一个半径为米的圆形喷水池,在池中心竖直安装一根水管,在水管的顶端点处安一个喷水头,测得喷水头距地面的高度为,水柱在距喷水头水平距离处达到最高,建立如图所示的平面直角坐标系,并设抛物线的表达式为,其中是水柱距喷水头的水平距离,是水柱距地面的高度.
(1)求抛物线的表达式;
(2)请你通过计算说明喷出的水柱是否会落到圆形喷水池的外面.
17.姣姣进行铅球专业训练,教练员尝试用数学模型来研究铅球的运动情况,从而做出指导.如图是姣姣在某次比赛前训练时,铅球行进高度与水平距离之间的函数图象,铅球经过的路径可以看作抛物线.铅球在距离地面的A处出手,在距离出手点A水平距离处(即)达到最高点,这次训练的成绩是.
(1)求这次训练中铅球经过路径的函数表达式;
(2)求这次训练中,铅球距离地面的最大高度为多少;
(3)这次训练中,铅球抛出的水平距离多大时,铅球离地面的高度为?
参考答案
1--8CDBDD CAC
9.
10.
11.6
12.13
13.
14.(1)解:小兵扔的小石头能击中点,理由如下:
根据题意,可得:抛物线的对称轴为,
又根据题意,可得:,,
点和点关于对称,
点在抛物线上,
小兵扔的小石头能击中点;
(2)解:根据题意,可得:抛物线的顶点坐标为,
设抛物线的解析式为,
又点经过抛物线,
把的坐标代入解析式,可得:,
解得:,
抛物线的解析式为,
又根据题意,可得:该抛物线的自变量的取值范围为,
小石头运动轨迹所在抛物线的解析式为,
(3)解:如图,连接,设直线的解析式为,
把代入,可得:,
解得:,
直线的解析式为,
设直线上方的抛物线上的一点的坐标为,
过点作轴,交于点,则的坐标为,
,
当时,有最大值,最大值为,
小石头在运动过程中与直线的最大竖直距离为.
15.(1)设从2016年到2018年,东营市用于充电桩安装的资金年平均增长率为x,
根据题意得:,
解得:,(舍去).
答:从2016年到2018年,东营市用于充电桩安装的资金年平均增长率为50%;
(2)设安装A型充电桩a个,则安装B型充电桩个,所需资金为万元.
根据题意,得:,
解得:,
,
∵,
∴随a的增大而减小.
∵a为整数,
∴当时,最小,最小值为(万元).
此时,.
答:A、B两种型号充电桩分别安装66个,134个时,所需资金最少,最少为767万元.
16.(1)由题意可知,抛物线的顶点坐标为,
则,,
抛物线的表达式为,
将代入上式得,,
解得,,
抛物线的表达式为.
(2)当时,,
解得,,舍去,
,
喷出的水柱不会落到圆形喷水池的外面.
17.(1)解:如下如图所示:设经过的路径与地面的交点为D,
依题意得:,,
∵在距离出手点A水平距离处(即)达到最高点,
∴图象的对称轴是直线,即直线
设这次训练中铅球经过路径的函数表达式为:
将点,代入得:
解得:
∴这次训练中铅球经过路径的函数表达式为:
(2)∵,
∴当时,
答:这次训练中,铅球距离地面的最大高度为.
(3)令,
解得:
答:这次训练中,铅球抛出的水平距离或时,铅球离地面的高度为.
同课章节目录
