11.2.1.2 直角三角形的性质与判定同步训练(含答案)【知识梳理+例题+练习】
文档属性
| 名称 | 11.2.1.2 直角三角形的性质与判定同步训练(含答案)【知识梳理+例题+练习】 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-20 17:05:49 | ||
图片预览




文档简介
11.2 与三角形有关的角
11.2.1 三角形的内角
第2课时 直角三角形的性质与判定
【知识重点】
1.直角三角形的性质 直角三角形的两个锐角互余 .
几何语言:在△ABC中,
∵∠C=90°,∴∠A+∠B=90°.
2.直角三角形的表示 直角三角形可以用符号“Rt △”表示,直角三角形ABC可以写成Rt △ABC.
注意:“Rt △”后必须紧跟表示直角三角形的三个顶点的大写字母,不能单独使用.如“直角三角形的边”不能写成“Rt△的边”.
3.直角三角形的判定 有两个角互余的三角形是直角三
角形.
特别解读:在直角三角形中,若已知两个锐角之间的数量关系,可结合两个锐角互余求出每个锐角的大小,不需要再利用三角形内角和定理求解.
【经典例题】
【例1】如图,AB,CD相交于点O,AC⊥CD于点C,若∠BOD=35°,则∠A=_______.
解题秘方:根据直角三角形中两锐角之间的数量关系求出角的度数.
【例2】如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P. 求证:△EFP是直角三角形.
解题秘方:如果三角形中有两个角的和等于90°(互余)就可证明该三角形为直角三角形.
【例3】如图,在△ABC中,∠ACB=90°,∠ACD=∠B. 求证:CD⊥AB.
解题秘方:利用直角三角形的性质与判定求出CD,AB 的夹角为直角.
【同步练习】
一、选择题
1.把一把直尺与一块三角板按如图所示的方式放置,若∠1=45°,则∠2的度数为( )
A.65° B.60° C.45° D.30°
第1题图 第2题图 第5题图
2.如图,AD是Rt△ABC的斜边BC上的高,则图中与∠B互余的角有( )
A.1个 B.2个 C.3个 D.4个
3.在一个直角三角形中,有一个锐角等于60°,则另一个锐角的度数是( )
A.120° B.90° C.60° D.30°
4.已知∠A=37°,∠B=53°,则△ABC为( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.以上都有可能
5.【2021·毕节】将一副三角尺按如图所示的位置摆放在直尺上,则∠1的度数为( )
A.70° B.75° C.80° D.85°
6.下列条件中,能判定△ABC为直角三角形的是 ( )
A.∠A=2∠B=3∠C B.∠A+∠B=2∠C
C.∠A=∠B=30° D.∠A=∠B=∠C
7.具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C B.∠A=∠B=∠C
C.∠A∶∠B∶∠C=1∶2∶3 D.∠A=2∠B=3∠C
8.直角三角形的三个内角的度数之比可以是 ( )
A.2∶3∶4 B.3∶4∶5 C.4∶5∶6 D.3∶3∶6
9.如图,AB∥CD,EF与AB,CD分别相交于点E,F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=50°,则∠EPF=( )度.
A.70 B.65 C.60 D.55
第9题图 第13题图 第14题图
10.具备下列条件的△ABC中,不是直角三角形的是 ( )
A.∠A+∠B=∠C B.∠A-∠B=∠C
C.∠A ∶∠B ∶∠C=1∶2∶3 D.∠A=∠B=3∠C
二、填空题
11.直角三角形的两个锐角________.直角三角形可以用符号“________”表示,直角三角形ABC可以写成__________.
12.在直角三角形中,一个锐角是另一个锐角的2倍,则此三角形中最小的角是 .
13.如图,点P是∠NOM的边OM上一点,PD⊥ON于点D,∠OPD=30°,PQ∥ON,则∠MPQ的度数是 .
14.如图,已知∠AOD=30°,点C是射线OD上的一个动点.在点C的运动过程中,△AOC恰好是直角三角形,则此时∠A所有可能的度数为 .
三、解答题
15.如图,点E是△ABC中AC边上的一点,过E作ED⊥AB,垂足为D.若∠1=∠2,则△ABC是直角三角形吗?为什么?
16.如图,在△ABC中,已知∠ACB=67°,BE是AC上的高,CD是AB上的高,F是BE和CD的交点,∠DCB=45°.求∠ABE的度数.
17.如图,在Rt△ABC中,∠BAC=90°,D为BC上一点,BF平分∠ABC,分别交AD,AC于点E,F,且∠AEF=∠AFE.求证:△BED是直角三角形.
18.如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P.试说明△EFP为直角三角形.
19.【2021·广陵区校级期中】已知:如图①,在△ABC中,CD是高,若∠A=∠DCB.
(1)试判断△ABC的形状,并说明理由;
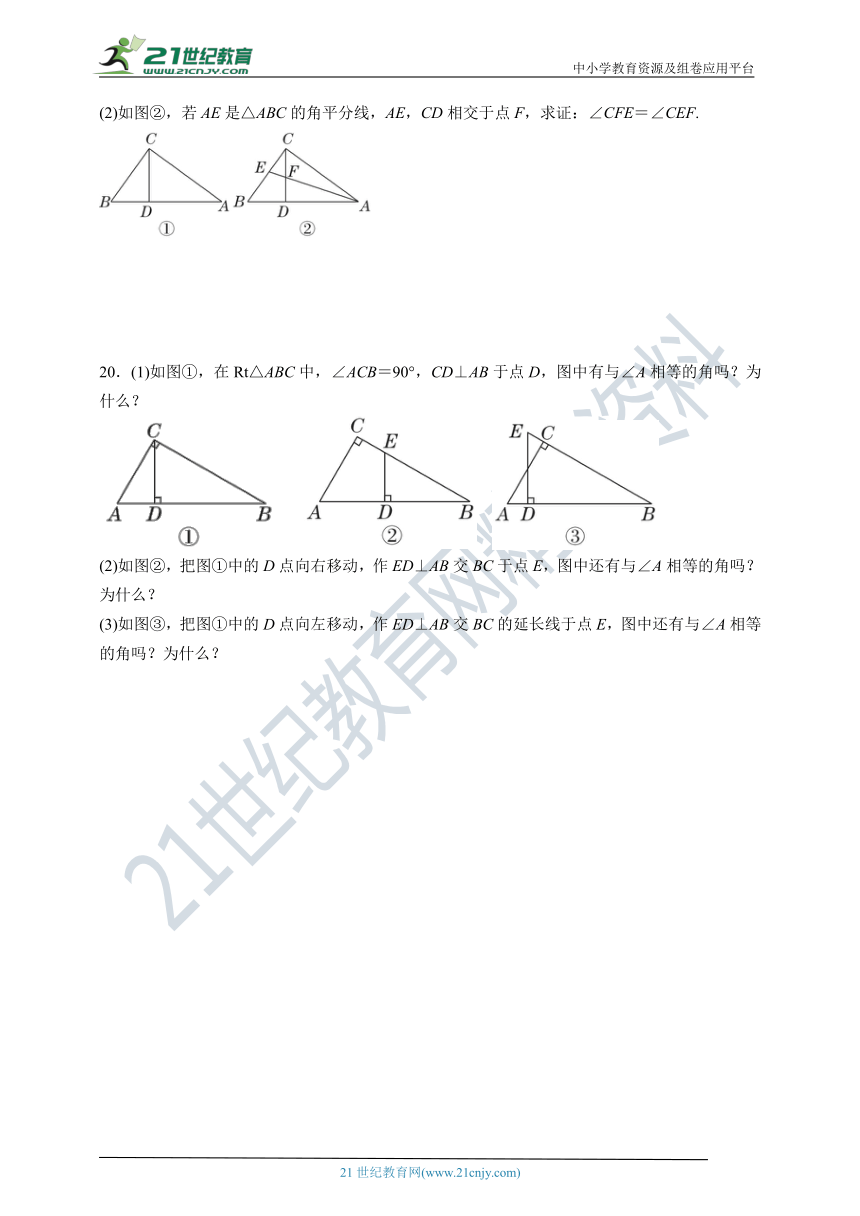
(2)如图②,若AE是△ABC的角平分线,AE,CD相交于点F,求证:∠CFE=∠CEF.
20.(1)如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,图中有与∠A相等的角吗?为什么?
(2)如图②,把图①中的D点向右移动,作ED⊥AB交BC于点E,图中还有与∠A相等的角吗?为什么?
(3)如图③,把图①中的D点向左移动,作ED⊥AB交BC的延长线于点E,图中还有与∠A相等的角吗?为什么?
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例1】如图,AB,CD相交于点O,AC⊥CD于点C,若∠BOD=35°,则∠A=_______.
解题秘方:根据直角三角形中两锐角之间的数量关系求出角的度数.
解:∵∠BOD=35°,∴∠AOC=35° .
又∵ AC⊥CD,∴∠ACD=90° .
∴ ∠A=90° -∠AOC=90°-35°=55° .
【例2】如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P. 求证:△EFP是直角三角形.
解题秘方:如果三角形中有两个角的和等于90°(互余)就可证明该三角形为直角三角形.
证明:∵ AB∥CD,∴∠BEF+∠DFE=180°.
又∵ EP平分∠BEF,FP 平分∠DFE,
∴∠PEF=∠BEF,∠PFE=∠DFE.
∴∠PEF+∠PFE= (∠BEF+∠DFE)=×180°=90°.
∴△EFP是直角三角形.
【例3】如图,在△ABC中,∠ACB=90°,∠ACD=∠B. 求证:CD⊥AB.
解题秘方:利用直角三角形的性质与判定求出CD,AB 的夹角为直角.
证明:∵∠ACB=90°,∴∠A+∠B=90°.
∵∠ACD=∠B,∴∠A+∠ACD=90°.
∴∠CDA=90°. ∴ CD⊥AB.
【同步练习】
一、选择题
1.把一把直尺与一块三角板按如图所示的方式放置,若∠1=45°,则∠2的度数为( C )
A.65° B.60° C.45° D.30°
第1题图 第2题图 第5题图
2.如图,AD是Rt△ABC的斜边BC上的高,则图中与∠B互余的角有( B )
A.1个 B.2个 C.3个 D.4个
3.在一个直角三角形中,有一个锐角等于60°,则另一个锐角的度数是( D )
A.120° B.90° C.60° D.30°
4.已知∠A=37°,∠B=53°,则△ABC为( C )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.以上都有可能
5.【2021·毕节】将一副三角尺按如图所示的位置摆放在直尺上,则∠1的度数为( B )
A.70° B.75° C.80° D.85°
6.下列条件中,能判定△ABC为直角三角形的是 ( D )
A.∠A=2∠B=3∠C B.∠A+∠B=2∠C
C.∠A=∠B=30° D.∠A=∠B=∠C
7.具备下列条件的△ABC中,不是直角三角形的是( D )
A.∠A+∠B=∠C B.∠A=∠B=∠C
C.∠A∶∠B∶∠C=1∶2∶3 D.∠A=2∠B=3∠C
8.直角三角形的三个内角的度数之比可以是 ( D )
A.2∶3∶4 B.3∶4∶5 C.4∶5∶6 D.3∶3∶6
9.如图,AB∥CD,EF与AB,CD分别相交于点E,F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=50°,则∠EPF=( A )度.
A.70 B.65 C.60 D.55
第9题图 第13题图 第14题图
10.具备下列条件的△ABC中,不是直角三角形的是 ( D )
A.∠A+∠B=∠C B.∠A-∠B=∠C
C.∠A ∶∠B ∶∠C=1∶2∶3 D.∠A=∠B=3∠C
二、填空题
11.直角三角形的两个锐角________.直角三角形可以用符号“________”表示,直角三角形ABC可以写成__________.
【答案】 互余 Rt△ Rt△ABC
12.在直角三角形中,一个锐角是另一个锐角的2倍,则此三角形中最小的角是 .
【答案】30°
13.如图,点P是∠NOM的边OM上一点,PD⊥ON于点D,∠OPD=30°,PQ∥ON,则∠MPQ的度数是 .
【答案】60°
14.如图,已知∠AOD=30°,点C是射线OD上的一个动点.在点C的运动过程中,△AOC恰好是直角三角形,则此时∠A所有可能的度数为 .
【答案】60°或90°
三、解答题
15.如图,点E是△ABC中AC边上的一点,过E作ED⊥AB,垂足为D.若∠1=∠2,则△ABC是直角三角形吗?为什么?
解:△ABC是直角三角形.
理由如下:
∵ED⊥AB,∴∠ADE=90°,
△ADE是直角三角形.
∴∠1+∠A=90°.
又∵∠1=∠2,
∴∠2+∠A=90°.
∴△ABC是直角三角形.
16.如图,在△ABC中,已知∠ACB=67°,BE是AC上的高,CD是AB上的高,F是BE和CD的交点,∠DCB=45°.求∠ABE的度数.
解:∵CD是AB上的高,
∴∠DBC=90°-∠DCB=90°-45°=45°.
∵BE是AC上的高,
∴∠EBC=90°-∠ECB=90°-67°=23°.
∴∠ABE=∠ABC-∠EBC=45°-23°=22°.
17.如图,在Rt△ABC中,∠BAC=90°,D为BC上一点,BF平分∠ABC,分别交AD,AC于点E,F,且∠AEF=∠AFE.求证:△BED是直角三角形.
证明:∵在Rt△ABF中,∠BAF=90°,
∴∠ABF+∠AFE=90°.
∵BF平分∠ABC,∴∠ABF=∠EBD.
∵∠AEF=∠AFE,∠BED=∠AEF,
∴∠BED=∠AFE.∴∠EBD+∠BED=90°.
∴△BED是直角三角形.
18.如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P.试说明△EFP为直角三角形.
解:∵AB∥CD,∴∠BEF+∠DFE=180°.
∵EP为∠BEF的平分线,FP为∠EFD的平分线,
∴∠PEF=∠BEF,∠PFE=∠DFE.
∴∠PEF+∠PFE=(∠BEF+∠DFE)=×180°=90°.
∴∠EPF=180°-(∠PEF+∠PFE)=90°.
∴△EFP为直角三角形.
19.【2021·广陵区校级期中】已知:如图①,在△ABC中,CD是高,若∠A=∠DCB.
(1)试判断△ABC的形状,并说明理由;
解:△ABC是直角三角形,理由如下:
在△ABC中,CD是高,
∴∠CDA=90°,∴∠A+∠ACD=90°.
∵∠A=∠DCB,∴∠DCB+∠ACD=90°.
∴∠ACB=90°.∴△ABC是直角三角形.
(2)如图②,若AE是△ABC的角平分线,AE,CD相交于点F,求证:∠CFE=∠CEF.
证明:∵AE是△ABC的角平分线,
∴∠DAF=∠CAE.
∵∠FDA=90°,∠ACE=90°,
∴∠DAF+∠AFD=90°,∠CAE+∠CEA=90°,
∴∠AFD=∠CEA.
∵∠AFD=∠CFE,∴∠CFE=∠CEA,
即∠CFE=∠CEF.
20.(1)如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,图中有与∠A相等的角吗?为什么?
解:有.
理由:∵CD⊥AB,∴∠B+∠BCD=90°.
∵∠ACB=90°,
∴∠B+∠A=90°.∴∠BCD=∠A.
(2)如图②,把图①中的D点向右移动,作ED⊥AB交BC于点E,图中还有与∠A相等的角吗?为什么?
解:有.
理由:∵ED⊥AB,∴∠B+∠BED=90°.
∵∠ACB=90°,
∴∠B+∠A=90°.∴∠BED=∠A.
(3)如图③,把图①中的D点向左移动,作ED⊥AB交BC的延长线于点E,图中还有与∠A相等的角吗?为什么?
解:有.
理由:∵ED⊥AB,∴∠B+∠E=90°.
∵∠ACB=90°,
∴∠B+∠A=90°.∴∠E=∠A.
11.2.1 三角形的内角
第2课时 直角三角形的性质与判定
【知识重点】
1.直角三角形的性质 直角三角形的两个锐角互余 .
几何语言:在△ABC中,
∵∠C=90°,∴∠A+∠B=90°.
2.直角三角形的表示 直角三角形可以用符号“Rt △”表示,直角三角形ABC可以写成Rt △ABC.
注意:“Rt △”后必须紧跟表示直角三角形的三个顶点的大写字母,不能单独使用.如“直角三角形的边”不能写成“Rt△的边”.
3.直角三角形的判定 有两个角互余的三角形是直角三
角形.
特别解读:在直角三角形中,若已知两个锐角之间的数量关系,可结合两个锐角互余求出每个锐角的大小,不需要再利用三角形内角和定理求解.
【经典例题】
【例1】如图,AB,CD相交于点O,AC⊥CD于点C,若∠BOD=35°,则∠A=_______.
解题秘方:根据直角三角形中两锐角之间的数量关系求出角的度数.
【例2】如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P. 求证:△EFP是直角三角形.
解题秘方:如果三角形中有两个角的和等于90°(互余)就可证明该三角形为直角三角形.
【例3】如图,在△ABC中,∠ACB=90°,∠ACD=∠B. 求证:CD⊥AB.
解题秘方:利用直角三角形的性质与判定求出CD,AB 的夹角为直角.
【同步练习】
一、选择题
1.把一把直尺与一块三角板按如图所示的方式放置,若∠1=45°,则∠2的度数为( )
A.65° B.60° C.45° D.30°
第1题图 第2题图 第5题图
2.如图,AD是Rt△ABC的斜边BC上的高,则图中与∠B互余的角有( )
A.1个 B.2个 C.3个 D.4个
3.在一个直角三角形中,有一个锐角等于60°,则另一个锐角的度数是( )
A.120° B.90° C.60° D.30°
4.已知∠A=37°,∠B=53°,则△ABC为( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.以上都有可能
5.【2021·毕节】将一副三角尺按如图所示的位置摆放在直尺上,则∠1的度数为( )
A.70° B.75° C.80° D.85°
6.下列条件中,能判定△ABC为直角三角形的是 ( )
A.∠A=2∠B=3∠C B.∠A+∠B=2∠C
C.∠A=∠B=30° D.∠A=∠B=∠C
7.具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C B.∠A=∠B=∠C
C.∠A∶∠B∶∠C=1∶2∶3 D.∠A=2∠B=3∠C
8.直角三角形的三个内角的度数之比可以是 ( )
A.2∶3∶4 B.3∶4∶5 C.4∶5∶6 D.3∶3∶6
9.如图,AB∥CD,EF与AB,CD分别相交于点E,F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=50°,则∠EPF=( )度.
A.70 B.65 C.60 D.55
第9题图 第13题图 第14题图
10.具备下列条件的△ABC中,不是直角三角形的是 ( )
A.∠A+∠B=∠C B.∠A-∠B=∠C
C.∠A ∶∠B ∶∠C=1∶2∶3 D.∠A=∠B=3∠C
二、填空题
11.直角三角形的两个锐角________.直角三角形可以用符号“________”表示,直角三角形ABC可以写成__________.
12.在直角三角形中,一个锐角是另一个锐角的2倍,则此三角形中最小的角是 .
13.如图,点P是∠NOM的边OM上一点,PD⊥ON于点D,∠OPD=30°,PQ∥ON,则∠MPQ的度数是 .
14.如图,已知∠AOD=30°,点C是射线OD上的一个动点.在点C的运动过程中,△AOC恰好是直角三角形,则此时∠A所有可能的度数为 .
三、解答题
15.如图,点E是△ABC中AC边上的一点,过E作ED⊥AB,垂足为D.若∠1=∠2,则△ABC是直角三角形吗?为什么?
16.如图,在△ABC中,已知∠ACB=67°,BE是AC上的高,CD是AB上的高,F是BE和CD的交点,∠DCB=45°.求∠ABE的度数.
17.如图,在Rt△ABC中,∠BAC=90°,D为BC上一点,BF平分∠ABC,分别交AD,AC于点E,F,且∠AEF=∠AFE.求证:△BED是直角三角形.
18.如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P.试说明△EFP为直角三角形.
19.【2021·广陵区校级期中】已知:如图①,在△ABC中,CD是高,若∠A=∠DCB.
(1)试判断△ABC的形状,并说明理由;
(2)如图②,若AE是△ABC的角平分线,AE,CD相交于点F,求证:∠CFE=∠CEF.
20.(1)如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,图中有与∠A相等的角吗?为什么?
(2)如图②,把图①中的D点向右移动,作ED⊥AB交BC于点E,图中还有与∠A相等的角吗?为什么?
(3)如图③,把图①中的D点向左移动,作ED⊥AB交BC的延长线于点E,图中还有与∠A相等的角吗?为什么?
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例1】如图,AB,CD相交于点O,AC⊥CD于点C,若∠BOD=35°,则∠A=_______.
解题秘方:根据直角三角形中两锐角之间的数量关系求出角的度数.
解:∵∠BOD=35°,∴∠AOC=35° .
又∵ AC⊥CD,∴∠ACD=90° .
∴ ∠A=90° -∠AOC=90°-35°=55° .
【例2】如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P. 求证:△EFP是直角三角形.
解题秘方:如果三角形中有两个角的和等于90°(互余)就可证明该三角形为直角三角形.
证明:∵ AB∥CD,∴∠BEF+∠DFE=180°.
又∵ EP平分∠BEF,FP 平分∠DFE,
∴∠PEF=∠BEF,∠PFE=∠DFE.
∴∠PEF+∠PFE= (∠BEF+∠DFE)=×180°=90°.
∴△EFP是直角三角形.
【例3】如图,在△ABC中,∠ACB=90°,∠ACD=∠B. 求证:CD⊥AB.
解题秘方:利用直角三角形的性质与判定求出CD,AB 的夹角为直角.
证明:∵∠ACB=90°,∴∠A+∠B=90°.
∵∠ACD=∠B,∴∠A+∠ACD=90°.
∴∠CDA=90°. ∴ CD⊥AB.
【同步练习】
一、选择题
1.把一把直尺与一块三角板按如图所示的方式放置,若∠1=45°,则∠2的度数为( C )
A.65° B.60° C.45° D.30°
第1题图 第2题图 第5题图
2.如图,AD是Rt△ABC的斜边BC上的高,则图中与∠B互余的角有( B )
A.1个 B.2个 C.3个 D.4个
3.在一个直角三角形中,有一个锐角等于60°,则另一个锐角的度数是( D )
A.120° B.90° C.60° D.30°
4.已知∠A=37°,∠B=53°,则△ABC为( C )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.以上都有可能
5.【2021·毕节】将一副三角尺按如图所示的位置摆放在直尺上,则∠1的度数为( B )
A.70° B.75° C.80° D.85°
6.下列条件中,能判定△ABC为直角三角形的是 ( D )
A.∠A=2∠B=3∠C B.∠A+∠B=2∠C
C.∠A=∠B=30° D.∠A=∠B=∠C
7.具备下列条件的△ABC中,不是直角三角形的是( D )
A.∠A+∠B=∠C B.∠A=∠B=∠C
C.∠A∶∠B∶∠C=1∶2∶3 D.∠A=2∠B=3∠C
8.直角三角形的三个内角的度数之比可以是 ( D )
A.2∶3∶4 B.3∶4∶5 C.4∶5∶6 D.3∶3∶6
9.如图,AB∥CD,EF与AB,CD分别相交于点E,F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=50°,则∠EPF=( A )度.
A.70 B.65 C.60 D.55
第9题图 第13题图 第14题图
10.具备下列条件的△ABC中,不是直角三角形的是 ( D )
A.∠A+∠B=∠C B.∠A-∠B=∠C
C.∠A ∶∠B ∶∠C=1∶2∶3 D.∠A=∠B=3∠C
二、填空题
11.直角三角形的两个锐角________.直角三角形可以用符号“________”表示,直角三角形ABC可以写成__________.
【答案】 互余 Rt△ Rt△ABC
12.在直角三角形中,一个锐角是另一个锐角的2倍,则此三角形中最小的角是 .
【答案】30°
13.如图,点P是∠NOM的边OM上一点,PD⊥ON于点D,∠OPD=30°,PQ∥ON,则∠MPQ的度数是 .
【答案】60°
14.如图,已知∠AOD=30°,点C是射线OD上的一个动点.在点C的运动过程中,△AOC恰好是直角三角形,则此时∠A所有可能的度数为 .
【答案】60°或90°
三、解答题
15.如图,点E是△ABC中AC边上的一点,过E作ED⊥AB,垂足为D.若∠1=∠2,则△ABC是直角三角形吗?为什么?
解:△ABC是直角三角形.
理由如下:
∵ED⊥AB,∴∠ADE=90°,
△ADE是直角三角形.
∴∠1+∠A=90°.
又∵∠1=∠2,
∴∠2+∠A=90°.
∴△ABC是直角三角形.
16.如图,在△ABC中,已知∠ACB=67°,BE是AC上的高,CD是AB上的高,F是BE和CD的交点,∠DCB=45°.求∠ABE的度数.
解:∵CD是AB上的高,
∴∠DBC=90°-∠DCB=90°-45°=45°.
∵BE是AC上的高,
∴∠EBC=90°-∠ECB=90°-67°=23°.
∴∠ABE=∠ABC-∠EBC=45°-23°=22°.
17.如图,在Rt△ABC中,∠BAC=90°,D为BC上一点,BF平分∠ABC,分别交AD,AC于点E,F,且∠AEF=∠AFE.求证:△BED是直角三角形.
证明:∵在Rt△ABF中,∠BAF=90°,
∴∠ABF+∠AFE=90°.
∵BF平分∠ABC,∴∠ABF=∠EBD.
∵∠AEF=∠AFE,∠BED=∠AEF,
∴∠BED=∠AFE.∴∠EBD+∠BED=90°.
∴△BED是直角三角形.
18.如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P.试说明△EFP为直角三角形.
解:∵AB∥CD,∴∠BEF+∠DFE=180°.
∵EP为∠BEF的平分线,FP为∠EFD的平分线,
∴∠PEF=∠BEF,∠PFE=∠DFE.
∴∠PEF+∠PFE=(∠BEF+∠DFE)=×180°=90°.
∴∠EPF=180°-(∠PEF+∠PFE)=90°.
∴△EFP为直角三角形.
19.【2021·广陵区校级期中】已知:如图①,在△ABC中,CD是高,若∠A=∠DCB.
(1)试判断△ABC的形状,并说明理由;
解:△ABC是直角三角形,理由如下:
在△ABC中,CD是高,
∴∠CDA=90°,∴∠A+∠ACD=90°.
∵∠A=∠DCB,∴∠DCB+∠ACD=90°.
∴∠ACB=90°.∴△ABC是直角三角形.
(2)如图②,若AE是△ABC的角平分线,AE,CD相交于点F,求证:∠CFE=∠CEF.
证明:∵AE是△ABC的角平分线,
∴∠DAF=∠CAE.
∵∠FDA=90°,∠ACE=90°,
∴∠DAF+∠AFD=90°,∠CAE+∠CEA=90°,
∴∠AFD=∠CEA.
∵∠AFD=∠CFE,∴∠CFE=∠CEA,
即∠CFE=∠CEF.
20.(1)如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,图中有与∠A相等的角吗?为什么?
解:有.
理由:∵CD⊥AB,∴∠B+∠BCD=90°.
∵∠ACB=90°,
∴∠B+∠A=90°.∴∠BCD=∠A.
(2)如图②,把图①中的D点向右移动,作ED⊥AB交BC于点E,图中还有与∠A相等的角吗?为什么?
解:有.
理由:∵ED⊥AB,∴∠B+∠BED=90°.
∵∠ACB=90°,
∴∠B+∠A=90°.∴∠BED=∠A.
(3)如图③,把图①中的D点向左移动,作ED⊥AB交BC的延长线于点E,图中还有与∠A相等的角吗?为什么?
解:有.
理由:∵ED⊥AB,∴∠B+∠E=90°.
∵∠ACB=90°,
∴∠B+∠A=90°.∴∠E=∠A.
