数学北师大版八年级下册 6.3《三角形的中位线》优秀教案
文档属性
| 名称 | 数学北师大版八年级下册 6.3《三角形的中位线》优秀教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 647.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 06:49:16 | ||
图片预览

文档简介
6.3《三角形的中位线》
一、教学目标
1.经历探索三角形中位线定理的过程,发展合情推理能力.
2. 证明三角形中位线定理,发展演绎推理能力
3.运用三角形中位线定理解决简单问题.
二、教学重点及难点
重点:三角形中位线及其定理的发现、探索及应用过程.
难点:掌握中位线在几何问题中的巧妙运用,把复杂图形转化为基本图形.
教学用具
多媒体课件、实物投影、三角尺、4个全等三角形纸片
相关资源
生活中的一些图片,微课,动画
五、教学过程
【情境导入】
1.(多媒体展示)你能将任意一个三角形分成四个全等的三角形吗?你能通过剪拼的方式,将一个三角形拼成一个与其面积相等的平行四边形吗?请同学们拿出自己准备好的三角形纸片试着分一下.
老师问:你是怎样做的?
学生答:连接每两边的中点.
老师问:你认为这样对吗?然后老师演示一遍,把四个三角形折叠在一起,四个三角形完全重合.
设计意图:在此过程中,学生会发现这里面有他们所熟悉的几何图形,图象既直观又形象,让学生充分体会到数学图形的美和数学与生活息息相关,从而引出今天研究的课题.
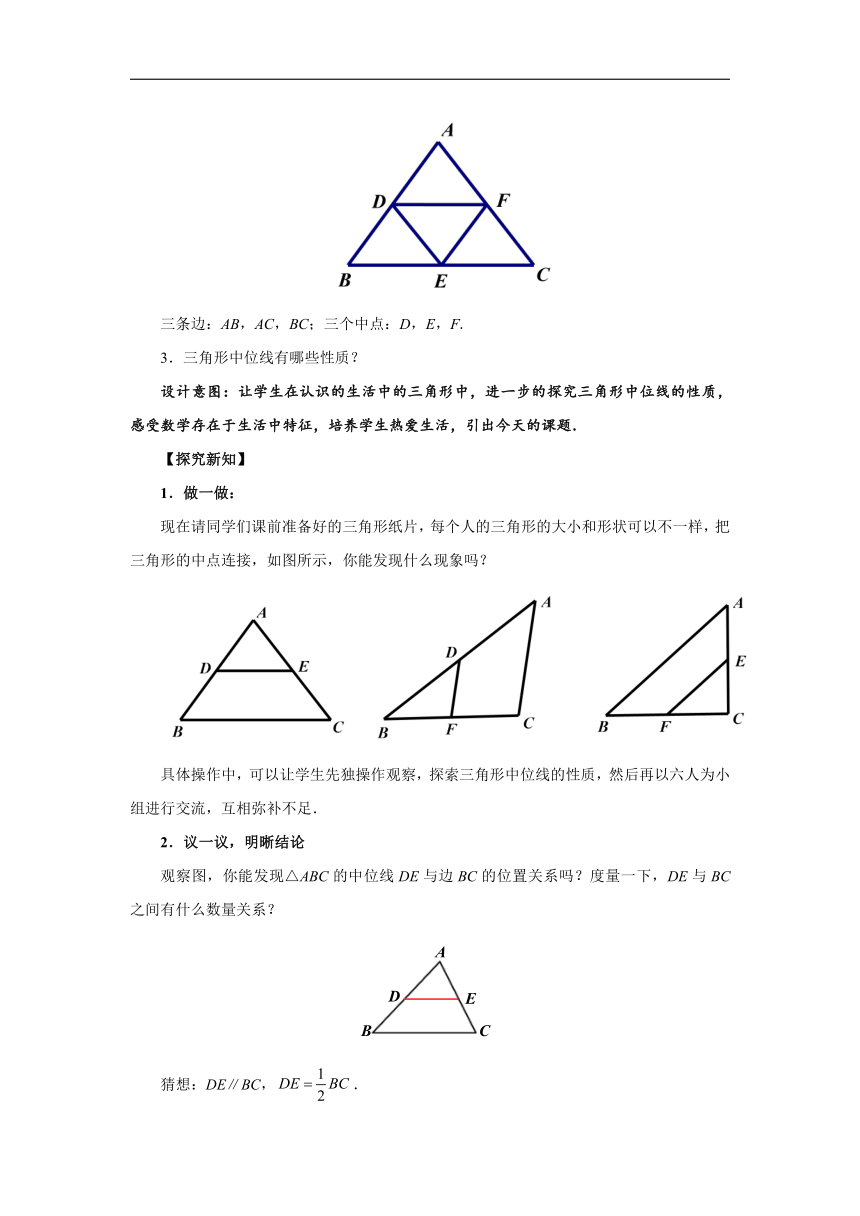
2.什么是三角形中位线?指出三角形的三边与中点.
三条边:AB,AC,BC;三个中点:D,E,F.
3.三角形中位线有哪些性质?
设计意图:让学生在认识的生活中的三角形中,进一步的探究三角形中位线的性质,感受数学存在于生活中特征,培养学生热爱生活,引出今天的课题.
【探究新知】
1.做一做:
现在请同学们课前准备好的三角形纸片,每个人的三角形的大小和形状可以不一样,把三角形的中点连接,如图所示,你能发现什么现象吗?
具体操作中,可以让学生先独操作观察,探索三角形中位线的性质,然后再以六人为小组进行交流,互相弥补不足.
2.议一议,明晰结论
观察图,你能发现△ABC的中位线DE与边BC的位置关系吗?度量一下,DE与BC之间有什么数量关系?
猜想:DE∥BC,.
这个结论如何证明是成立呢?请写出已知,求证并证明.
已知:DE是△ABC的中位线.
求证:DE∥BC,DE=BC.
生:学生独立思考解决问题的方法,有困难小组交流合作,互相补充.并独立完成解答.
师:出示多媒体答案,强调巡视时发现的问题.
证明:如图(2),延长DE到F ,使FE=DE,连接CF.
在△ADE和CFE中,
∵AE=CE,∠1=∠2,FE=DE,
∴△ADE≌CFE.
∴∠A=∠ECF,AD=CF.
∴CF∥AB.
∵BD=AD,
∴CF=BD.
∴四边形DBCF是平行四边形(一组对边平行且相等的四边形是平行四边形).
∴DF∥BC(平行四边形定义),
DF=BC(平行四边形对边相等).
∴DE∥BC,DE=BC.
通过上面的证明,我们得到
三角形中位线定理:三角形的中位线平行于第三边,且等于第三边的一半.
设计意图:通过设计“观察—猜想—总结—验证”这一过程,使学生经历从探究中抽象出数学概念的过程,同时也通过学生分组合作,培养协作能力.
【典例精讲】
例1已知三角形的各边长分别为8cm,10cm,12cm,求以各边中点为顶点的三角形的周长.
生:学生独立思考解决问题的方法,有困难小组交流合作,互相补充并独立完成解答.
师:出示多媒体答案,强调巡视时发现的问题.找学生板演步骤,师点拨.
解:如图,
设三角形及其中点如图所示,则由三角形中位线定理可得:
DE=BC,DF=AC,EF=AB,
∵AB +BC +AC=8cm+10cm+12cm=20cm.
∴DE +DF +EF=10cm(三角形中位线等于底边一半).
∴各边中点为顶点的三角形的周长为10cm.
设计意图:培养学生灵活运用知识解决问题的能力,鼓励学生在交流探索中发现证明方法的多样性,提高逻辑思维水平.
【课堂练习】
1.已知直角三角形的两条直角边长分别为6和8,则连接这两条直角边中点的线段长为( )
A.3 B.4 C.5 D.6
2.如图,D,E分别为△ABC的AC,BC边的中点,将此三角形沿DE折叠,使点C落在AB边上的点P处.若∠CDE=48°,则∠APD的度数是( )
A.42° B.48° C.52° D.58°
答案:
1.C. 2.B.
【课堂小结】
教师注意对学生的感想进行适当的引导,并在学生交流的基础上,明晰部分收获供学生共享;如:
1.通过动手活动对获得的定理给予了直观的感受,为今后解决有关三角形中位线的问题提供了丰富的理论依据.
(1)三角形中位线平行于第三边.
(2)三角形中位线等于第三边的一半.
2.体会了证明一个命题的严格的要求,体会了证明的必要性.
【板书设计】
三角形中位线定理:三角形的中位线平行于第三边,且等于第三边的一半.
例:设三角形及其中点如图所示,则由三角形中位线定理可得:
DE=BC,DF=AC,EF=AB,
∵AB +BC +AC=8cm+10cm+12cm=20cm.
∴DE +DF +EF=10cm(三角形中位线等于底边一半).
∴各边中点为顶点的三角形的周长为10cm.
一、教学目标
1.经历探索三角形中位线定理的过程,发展合情推理能力.
2. 证明三角形中位线定理,发展演绎推理能力
3.运用三角形中位线定理解决简单问题.
二、教学重点及难点
重点:三角形中位线及其定理的发现、探索及应用过程.
难点:掌握中位线在几何问题中的巧妙运用,把复杂图形转化为基本图形.
教学用具
多媒体课件、实物投影、三角尺、4个全等三角形纸片
相关资源
生活中的一些图片,微课,动画
五、教学过程
【情境导入】
1.(多媒体展示)你能将任意一个三角形分成四个全等的三角形吗?你能通过剪拼的方式,将一个三角形拼成一个与其面积相等的平行四边形吗?请同学们拿出自己准备好的三角形纸片试着分一下.
老师问:你是怎样做的?
学生答:连接每两边的中点.
老师问:你认为这样对吗?然后老师演示一遍,把四个三角形折叠在一起,四个三角形完全重合.
设计意图:在此过程中,学生会发现这里面有他们所熟悉的几何图形,图象既直观又形象,让学生充分体会到数学图形的美和数学与生活息息相关,从而引出今天研究的课题.
2.什么是三角形中位线?指出三角形的三边与中点.
三条边:AB,AC,BC;三个中点:D,E,F.
3.三角形中位线有哪些性质?
设计意图:让学生在认识的生活中的三角形中,进一步的探究三角形中位线的性质,感受数学存在于生活中特征,培养学生热爱生活,引出今天的课题.
【探究新知】
1.做一做:
现在请同学们课前准备好的三角形纸片,每个人的三角形的大小和形状可以不一样,把三角形的中点连接,如图所示,你能发现什么现象吗?
具体操作中,可以让学生先独操作观察,探索三角形中位线的性质,然后再以六人为小组进行交流,互相弥补不足.
2.议一议,明晰结论
观察图,你能发现△ABC的中位线DE与边BC的位置关系吗?度量一下,DE与BC之间有什么数量关系?
猜想:DE∥BC,.
这个结论如何证明是成立呢?请写出已知,求证并证明.
已知:DE是△ABC的中位线.
求证:DE∥BC,DE=BC.
生:学生独立思考解决问题的方法,有困难小组交流合作,互相补充.并独立完成解答.
师:出示多媒体答案,强调巡视时发现的问题.
证明:如图(2),延长DE到F ,使FE=DE,连接CF.
在△ADE和CFE中,
∵AE=CE,∠1=∠2,FE=DE,
∴△ADE≌CFE.
∴∠A=∠ECF,AD=CF.
∴CF∥AB.
∵BD=AD,
∴CF=BD.
∴四边形DBCF是平行四边形(一组对边平行且相等的四边形是平行四边形).
∴DF∥BC(平行四边形定义),
DF=BC(平行四边形对边相等).
∴DE∥BC,DE=BC.
通过上面的证明,我们得到
三角形中位线定理:三角形的中位线平行于第三边,且等于第三边的一半.
设计意图:通过设计“观察—猜想—总结—验证”这一过程,使学生经历从探究中抽象出数学概念的过程,同时也通过学生分组合作,培养协作能力.
【典例精讲】
例1已知三角形的各边长分别为8cm,10cm,12cm,求以各边中点为顶点的三角形的周长.
生:学生独立思考解决问题的方法,有困难小组交流合作,互相补充并独立完成解答.
师:出示多媒体答案,强调巡视时发现的问题.找学生板演步骤,师点拨.
解:如图,
设三角形及其中点如图所示,则由三角形中位线定理可得:
DE=BC,DF=AC,EF=AB,
∵AB +BC +AC=8cm+10cm+12cm=20cm.
∴DE +DF +EF=10cm(三角形中位线等于底边一半).
∴各边中点为顶点的三角形的周长为10cm.
设计意图:培养学生灵活运用知识解决问题的能力,鼓励学生在交流探索中发现证明方法的多样性,提高逻辑思维水平.
【课堂练习】
1.已知直角三角形的两条直角边长分别为6和8,则连接这两条直角边中点的线段长为( )
A.3 B.4 C.5 D.6
2.如图,D,E分别为△ABC的AC,BC边的中点,将此三角形沿DE折叠,使点C落在AB边上的点P处.若∠CDE=48°,则∠APD的度数是( )
A.42° B.48° C.52° D.58°
答案:
1.C. 2.B.
【课堂小结】
教师注意对学生的感想进行适当的引导,并在学生交流的基础上,明晰部分收获供学生共享;如:
1.通过动手活动对获得的定理给予了直观的感受,为今后解决有关三角形中位线的问题提供了丰富的理论依据.
(1)三角形中位线平行于第三边.
(2)三角形中位线等于第三边的一半.
2.体会了证明一个命题的严格的要求,体会了证明的必要性.
【板书设计】
三角形中位线定理:三角形的中位线平行于第三边,且等于第三边的一半.
例:设三角形及其中点如图所示,则由三角形中位线定理可得:
DE=BC,DF=AC,EF=AB,
∵AB +BC +AC=8cm+10cm+12cm=20cm.
∴DE +DF +EF=10cm(三角形中位线等于底边一半).
∴各边中点为顶点的三角形的周长为10cm.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
