北师大版数学八年级下册 1.3线段的垂直平分线 (第1课时)教案
文档属性
| 名称 | 北师大版数学八年级下册 1.3线段的垂直平分线 (第1课时)教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 785.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 09:20:08 | ||
图片预览


文档简介
第一章 三角形的证明
1.3 线段的垂直平分线
第1课时
一、教学目标
1.经历“探索—发现—猜想—证明”的过程,进一步体会证明的必要性,增强证明意识和能力.
2.证明线段垂直平分线的性质定理,探索并证明线段垂直平分线的判定定理,进一步发展推理能力.
二、教学重点及难点
重点:线段垂直平分线的性质和判定.
难点:证明线段的垂直平分线的性质和判定解题.
三、教学用具
多媒体课件、直尺或三角板.
四、相关资源
微课,知识卡片图片.
五、教学过程
【情境导入】
如图,A,B表示路边的两个花店,要在A,B一侧建造一个花卉基地,使它到两个花店的距离相等,花卉基地应建在什么位置
其中“到两个花店的距离相等”,要强调这几个字在题中有很重要的作用.
线段是一个轴对称图形,其中线段的垂直平分线就是它的对称轴.我们曾经用折纸的方法,根据折叠过程中线段重合说明了线段垂直平分线的一个性质:线段垂直平分线上的点到这条线段两个端点的距离相等.所以在这个问题中,要求在“A,B一侧建造一个花卉基地,使它到两个花店的距离相等”利用此性质就能完成.
请尝试证明线段垂直平分线的性质定理,并与同伴交流.
设计意图:通过问题,让学生在解决问题的同时,回顾线段垂直平分线的性质及探索过程.
【探究新知】
1.证明:线段垂直平分线上的点到这条线段两个端点的距离相等
师:能用我们已有的知识来证明这个定理吗?
学生讨论给出证明.教师请两位学生黑板板演,集体纠正,并用多媒体展示正确答案.
已知:如图,直线MN⊥ AB,垂足为C,且AC=BC,P是MN上的任意一点.
求证:PA=PB.
证明:∵ MN⊥ AB,
∴ ∠ PCA=∠ PCB=90°.
又∵AC=CB,PC=PC,
∴ △ PCA≌ △ PCB(SAS).
∴PA=PB(全等三角形的对应边相等).
定理:线段垂直平分线上的点到这条线段两个端点的距离相等.
几何语言:
∵ AC=BC,MN⊥ AB,
∴ PA=PB.
2.想一想
能写出上面这个定理的逆命题吗?它是真命题吗?如果是,请加以证明.
生:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
师:你能证明上面的结论吗?
学生讨论给出证明.学生黑板板演,教师多媒体展示证明过程,对比学生解答,纠正问题.
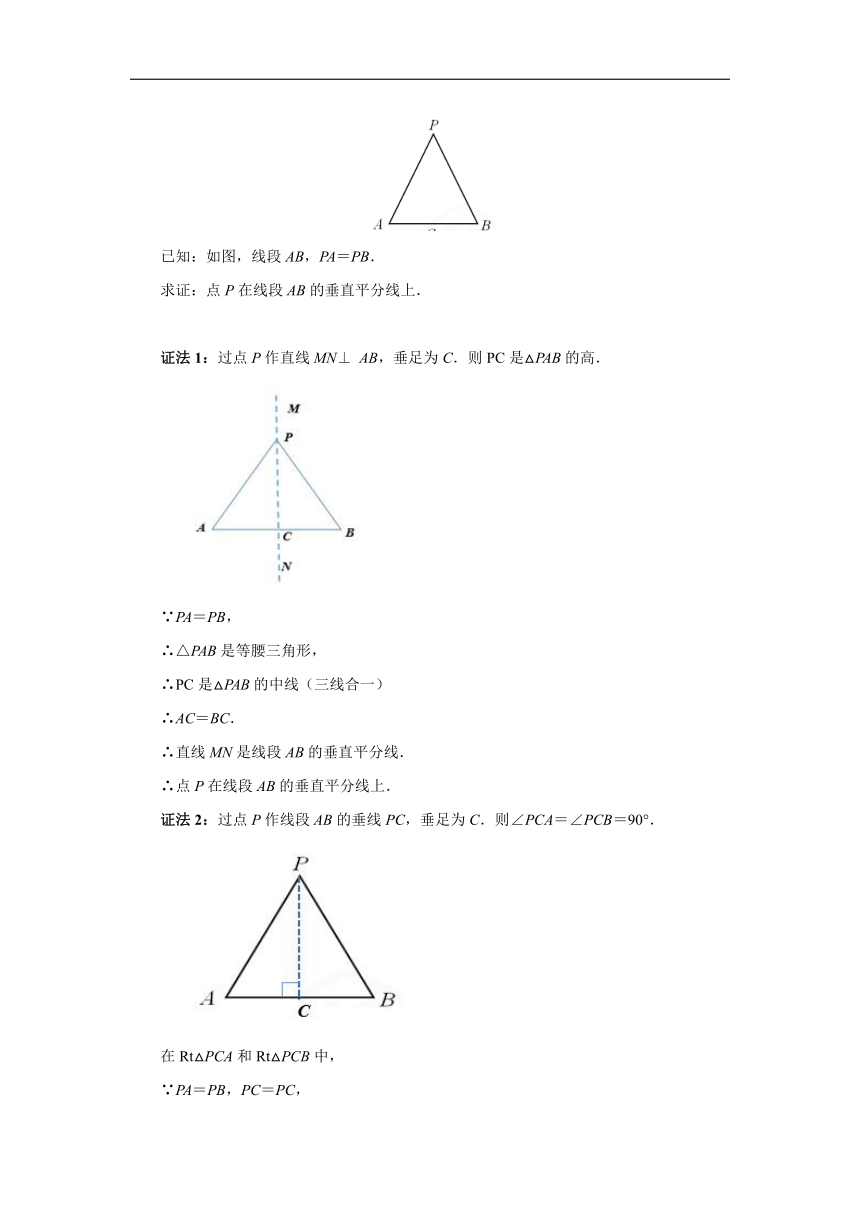
已知:如图,线段AB,PA=PB.
求证:点P在线段AB的垂直平分线上.
证法1:过点P作直线MN⊥ AB,垂足为C.则PC是△PAB的高.
∵PA=PB,
∴△PAB是等腰三角形,
∴PC是△PAB的中线(三线合一)
∴AC=BC.
∴直线MN是线段AB的垂直平分线.
∴点P在线段AB的垂直平分线上.
证法2:过点P作线段AB的垂线PC,垂足为C.则∠PCA=∠PCB=90°.
在Rt△PCA和Rt△PCB中,
∵PA=PB,PC=PC,
∴Rt△PCA≌Rt△PCB(HL).
∴AC=BC.
又PC⊥AB,
∴点P在线段AB的垂直平分线上.
证法3:
证明:取AB的中点C,过PC作直线.
∵AP=BP,PC=PC.AC=CB,
∴△APC≌△BPC(SSS).
∴∠PCA=∠PCB(全等三角形的对应角相等).
又∵∠PCA+∠PCB=180°,
∴∠PCA=∠PCB=∠90°,即PC⊥AB,
∴P点在AB的垂直平分线上.
证法4:
证明:过P点作∠APB的角平分线.
∵AP=BP,∠APC=∠BPC,PC=PC,
△APC≌△BPC(SAS).
∴AC=BC,∠PCA=∠PCB(全等三角形的对应角相等,对应边相等).
又∵∠PCA+∠PCB=180°,∴∠PCA=∠PCB=90°,
∴P点在线段AB的垂直平分线上.
判定定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
用数学符号表示为:
∵PA=PB,
∴点P在AB的垂直平分线上.
师:你能再找一些到线段AB两端点的距离相等的点吗?能找到多少个到线段AB两端点距离相等的点?这些点能组成什么几何图形?
生:在线段AB的垂直平分线l上的点与A,B的距离都相等;反过来,与A,B的距离相等的点都在直线l上,所以直线l可以看成与两点A,B的距离相等的所有点的集合.
设计意图:引导学生对性质定理进行逆向思考,提出猜想,然后加以证明.这是获得新的几何结论的一种常用方法.因为这个性质定理不是“如果……那么……”的形式,学生说出或写出它的逆命题可能会有一定的困难,可以引导学生分析它的条件和结论,再写出逆命题,最后由学生写出证明过程.
【典例精析】
例 已知:如图,在 △ABC 中,AB = AC,O 是 △ABC 内一点,且 OB = OC.
求证:直线 AO 垂直平分线段BC.
学生自主完成:
证明:∵ AB = AC,
∴ 点A在线段 BC 的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).
同理,点O在线段 BC 的垂直平分线上.
∴ 直线AO是线段 BC 的垂直平分线(两点确定一条直线).
设计意图:应用线段垂直平分线的性质定理,在解答过程中,引导学生分析解决问题的方法.可能有学生用全等三角形证明,此时应注意引导学生对比两种证明方法,体会线段垂直平分线的判定定理的作用.
【课堂练习】
1.三角形纸片上有一点P,量得PA=3 cm,PB=3 cm,则点P一定( ).
A.是边AB的中点 B.在边AB的中线上
C.在边AB的高上 D.在边AB的垂直平分线上
2.如图,在△ABC中,EF是AC的垂直平分线,AF=12,BF=3,则BC=__________.
3.如图,BD垂直平分CE,ED=3 cm,△ABE的周长为11 cm,则△ACE的周长为__________.
4.如图,△ABC中,BC=7,AB的垂直平分线分别交AB,BC于点D,E,AC的垂直平分线分别交AC,BC于点F,G.求△AEG的周长.
5.如下图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB、AC、CE的长度有什么关系?AB+BD与DE有什么关系?
6.如下图,AB=AC,MB=MC.直线AM是线段BC的垂直平分线吗?
设计意图:及时巩固所学知识,了解学生的学习效果,增强学生灵活运用知识的能力.
参考答案:
1.D.解析:点P到线段AB两个端点的距离相等,点P在线段AB的垂直平分线上.
2.15.3.17 cm.
4.解:DE,GF分别是AB,AC的垂直平分线,
∴BE=AE,CG=AG.
∴△AEG的周长=AE+EG+AG=BE+EG+CG=BC=7.
答:△AEG的周长为7.
5.解:∵AD⊥BC,BD=DC,
∴AD是BC的垂直平分线.
∴AB=AC.
∵点C在AE的垂直平分线上,
∴AC=CE.
∴AB=AC=CE.
∵AB=CE,BD=DC,
∴AB+BD=CD+CE.即AB+BD=DE.
6.解:∵AB=AC,
∴点A在BC的垂直平分线上.
∵MB=MC,
∴点M在BC的垂直平分线上.
∴直线AM是线段BC的垂直平分线.
六、课堂小结
1.性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等.
2.判定定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
设计意图:通过学生思考总结所学内容,培养学生归纳总结能力.
七、板书设计
1.3 线段的垂直平分线(1)
1.性质定理.
2.判定定理.
1.3 线段的垂直平分线
第1课时
一、教学目标
1.经历“探索—发现—猜想—证明”的过程,进一步体会证明的必要性,增强证明意识和能力.
2.证明线段垂直平分线的性质定理,探索并证明线段垂直平分线的判定定理,进一步发展推理能力.
二、教学重点及难点
重点:线段垂直平分线的性质和判定.
难点:证明线段的垂直平分线的性质和判定解题.
三、教学用具
多媒体课件、直尺或三角板.
四、相关资源
微课,知识卡片图片.
五、教学过程
【情境导入】
如图,A,B表示路边的两个花店,要在A,B一侧建造一个花卉基地,使它到两个花店的距离相等,花卉基地应建在什么位置
其中“到两个花店的距离相等”,要强调这几个字在题中有很重要的作用.
线段是一个轴对称图形,其中线段的垂直平分线就是它的对称轴.我们曾经用折纸的方法,根据折叠过程中线段重合说明了线段垂直平分线的一个性质:线段垂直平分线上的点到这条线段两个端点的距离相等.所以在这个问题中,要求在“A,B一侧建造一个花卉基地,使它到两个花店的距离相等”利用此性质就能完成.
请尝试证明线段垂直平分线的性质定理,并与同伴交流.
设计意图:通过问题,让学生在解决问题的同时,回顾线段垂直平分线的性质及探索过程.
【探究新知】
1.证明:线段垂直平分线上的点到这条线段两个端点的距离相等
师:能用我们已有的知识来证明这个定理吗?
学生讨论给出证明.教师请两位学生黑板板演,集体纠正,并用多媒体展示正确答案.
已知:如图,直线MN⊥ AB,垂足为C,且AC=BC,P是MN上的任意一点.
求证:PA=PB.
证明:∵ MN⊥ AB,
∴ ∠ PCA=∠ PCB=90°.
又∵AC=CB,PC=PC,
∴ △ PCA≌ △ PCB(SAS).
∴PA=PB(全等三角形的对应边相等).
定理:线段垂直平分线上的点到这条线段两个端点的距离相等.
几何语言:
∵ AC=BC,MN⊥ AB,
∴ PA=PB.
2.想一想
能写出上面这个定理的逆命题吗?它是真命题吗?如果是,请加以证明.
生:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
师:你能证明上面的结论吗?
学生讨论给出证明.学生黑板板演,教师多媒体展示证明过程,对比学生解答,纠正问题.
已知:如图,线段AB,PA=PB.
求证:点P在线段AB的垂直平分线上.
证法1:过点P作直线MN⊥ AB,垂足为C.则PC是△PAB的高.
∵PA=PB,
∴△PAB是等腰三角形,
∴PC是△PAB的中线(三线合一)
∴AC=BC.
∴直线MN是线段AB的垂直平分线.
∴点P在线段AB的垂直平分线上.
证法2:过点P作线段AB的垂线PC,垂足为C.则∠PCA=∠PCB=90°.
在Rt△PCA和Rt△PCB中,
∵PA=PB,PC=PC,
∴Rt△PCA≌Rt△PCB(HL).
∴AC=BC.
又PC⊥AB,
∴点P在线段AB的垂直平分线上.
证法3:
证明:取AB的中点C,过PC作直线.
∵AP=BP,PC=PC.AC=CB,
∴△APC≌△BPC(SSS).
∴∠PCA=∠PCB(全等三角形的对应角相等).
又∵∠PCA+∠PCB=180°,
∴∠PCA=∠PCB=∠90°,即PC⊥AB,
∴P点在AB的垂直平分线上.
证法4:
证明:过P点作∠APB的角平分线.
∵AP=BP,∠APC=∠BPC,PC=PC,
△APC≌△BPC(SAS).
∴AC=BC,∠PCA=∠PCB(全等三角形的对应角相等,对应边相等).
又∵∠PCA+∠PCB=180°,∴∠PCA=∠PCB=90°,
∴P点在线段AB的垂直平分线上.
判定定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
用数学符号表示为:
∵PA=PB,
∴点P在AB的垂直平分线上.
师:你能再找一些到线段AB两端点的距离相等的点吗?能找到多少个到线段AB两端点距离相等的点?这些点能组成什么几何图形?
生:在线段AB的垂直平分线l上的点与A,B的距离都相等;反过来,与A,B的距离相等的点都在直线l上,所以直线l可以看成与两点A,B的距离相等的所有点的集合.
设计意图:引导学生对性质定理进行逆向思考,提出猜想,然后加以证明.这是获得新的几何结论的一种常用方法.因为这个性质定理不是“如果……那么……”的形式,学生说出或写出它的逆命题可能会有一定的困难,可以引导学生分析它的条件和结论,再写出逆命题,最后由学生写出证明过程.
【典例精析】
例 已知:如图,在 △ABC 中,AB = AC,O 是 △ABC 内一点,且 OB = OC.
求证:直线 AO 垂直平分线段BC.
学生自主完成:
证明:∵ AB = AC,
∴ 点A在线段 BC 的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).
同理,点O在线段 BC 的垂直平分线上.
∴ 直线AO是线段 BC 的垂直平分线(两点确定一条直线).
设计意图:应用线段垂直平分线的性质定理,在解答过程中,引导学生分析解决问题的方法.可能有学生用全等三角形证明,此时应注意引导学生对比两种证明方法,体会线段垂直平分线的判定定理的作用.
【课堂练习】
1.三角形纸片上有一点P,量得PA=3 cm,PB=3 cm,则点P一定( ).
A.是边AB的中点 B.在边AB的中线上
C.在边AB的高上 D.在边AB的垂直平分线上
2.如图,在△ABC中,EF是AC的垂直平分线,AF=12,BF=3,则BC=__________.
3.如图,BD垂直平分CE,ED=3 cm,△ABE的周长为11 cm,则△ACE的周长为__________.
4.如图,△ABC中,BC=7,AB的垂直平分线分别交AB,BC于点D,E,AC的垂直平分线分别交AC,BC于点F,G.求△AEG的周长.
5.如下图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB、AC、CE的长度有什么关系?AB+BD与DE有什么关系?
6.如下图,AB=AC,MB=MC.直线AM是线段BC的垂直平分线吗?
设计意图:及时巩固所学知识,了解学生的学习效果,增强学生灵活运用知识的能力.
参考答案:
1.D.解析:点P到线段AB两个端点的距离相等,点P在线段AB的垂直平分线上.
2.15.3.17 cm.
4.解:DE,GF分别是AB,AC的垂直平分线,
∴BE=AE,CG=AG.
∴△AEG的周长=AE+EG+AG=BE+EG+CG=BC=7.
答:△AEG的周长为7.
5.解:∵AD⊥BC,BD=DC,
∴AD是BC的垂直平分线.
∴AB=AC.
∵点C在AE的垂直平分线上,
∴AC=CE.
∴AB=AC=CE.
∵AB=CE,BD=DC,
∴AB+BD=CD+CE.即AB+BD=DE.
6.解:∵AB=AC,
∴点A在BC的垂直平分线上.
∵MB=MC,
∴点M在BC的垂直平分线上.
∴直线AM是线段BC的垂直平分线.
六、课堂小结
1.性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等.
2.判定定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
设计意图:通过学生思考总结所学内容,培养学生归纳总结能力.
七、板书设计
1.3 线段的垂直平分线(1)
1.性质定理.
2.判定定理.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
