2022-2023学年沪科版七年级数学上册3.2一元一次方程的应用第1课时等积问题与行程问题 课件(共21张PPT)
文档属性
| 名称 | 2022-2023学年沪科版七年级数学上册3.2一元一次方程的应用第1课时等积问题与行程问题 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 09:26:27 | ||
图片预览






文档简介
(共21张PPT)
第3章 一次方程与方程组
第1课时 图形等积和变换问题
3.2 一元一次方程的应用
沪科版数学七年级上册
教学目标
【知识与技能】
1.通过分析图形问题中的基本等量关系,建立方程解决问题.
2.进一步了解一元一次方程在解决实际问题中的应用.
【过程与方法】
用实例对一些数学猜想做出检验,从而增加猜想的可信程度或推翻猜想.
【情感、态度与价值观】
培养学生敢于面对和克服数学活动中困难的能力,使他们拥有运用知识解决问题的成功体验,建立学好数学的自信心.
长方体的体积=长×宽×高;
正方体的体积=棱长×棱长×棱长;
圆柱体的体积=底面积×高=πr2h;
圆锥体的体积= ×底面积×高= πr2h.
知识回顾
常用的体积公式
新知导入
h
r
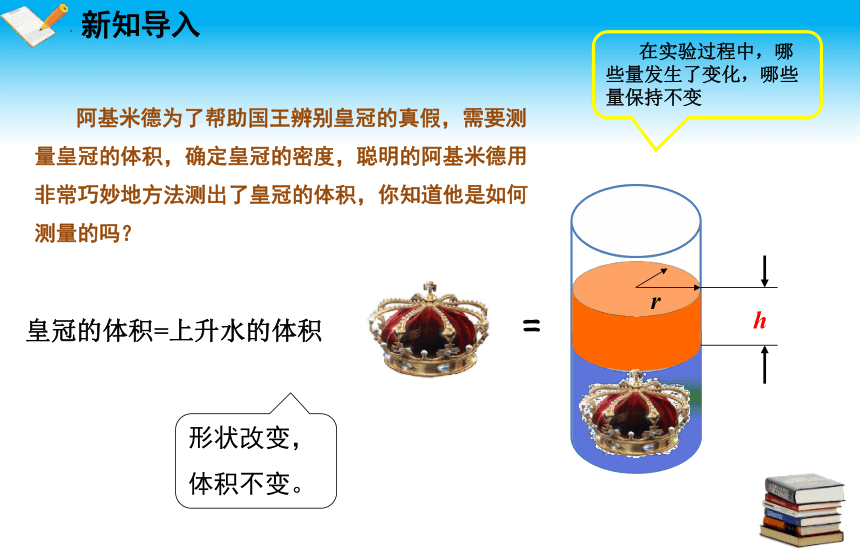
阿基米德为了帮助国王辨别皇冠的真假,需要测量皇冠的体积,确定皇冠的密度,聪明的阿基米德用非常巧妙地方法测出了皇冠的体积,你知道他是如何测量的吗?
=
形状改变,
体积不变。
在实验过程中,哪些量发生了变化,哪些量保持不变
皇冠的体积=上升水的体积
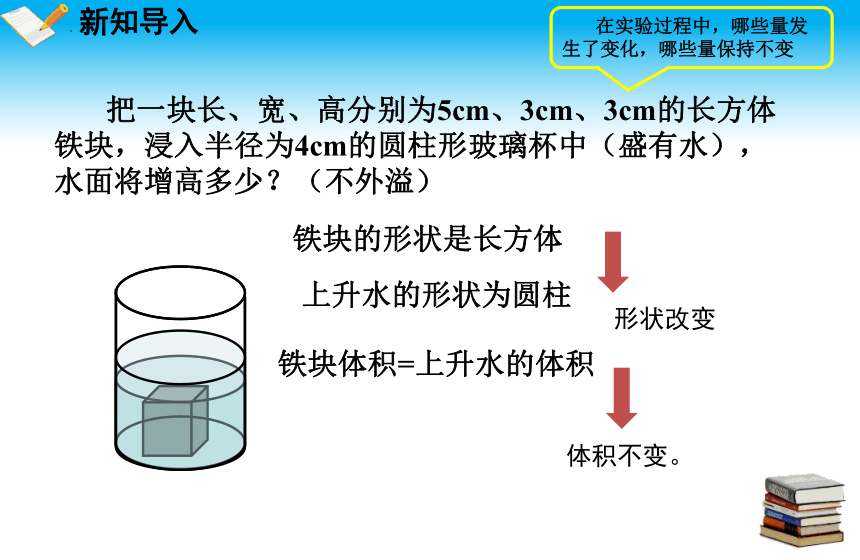
把一块长、宽、高分别为5cm、3cm、3cm的长方体铁块,浸入半径为4cm的圆柱形玻璃杯中(盛有水),水面将增高多少?(不外溢)
在实验过程中,哪些量发生了变化,哪些量保持不变
体积不变。
新知导入
铁块体积=上升水的体积
上升水的形状为圆柱
形状改变
铁块的形状是长方体
新知导入
请指出下列过程中,哪些量发生了变化,哪些量保持不变
(1)把一小杯水倒入另一只大杯中
(2)用一根15cm长的铁丝围成一个三角形,然后把它改围成长方形.
(3)用一块橡皮泥先做成一个立方体,再把它该做成球.
水的底面积和高度发生变化,水的体积和质量不变.
围成图形的面积发生变化,但铁丝长度不变.
形状发生改变,但体积不变。
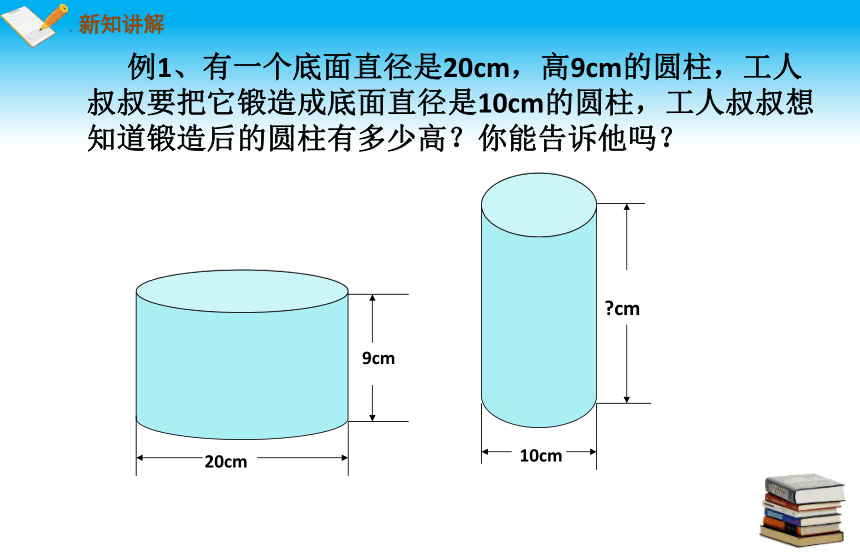
例1、有一个底面直径是20cm,高9cm的圆柱,工人叔叔要把它锻造成底面直径是10cm的圆柱,工人叔叔想知道锻造后的圆柱有多少高?你能告诉他吗?
20cm
9cm
10cm
cm
新知讲解
2、根据这个等量关系怎样列方程?
1、本题中有什么等量关系?
锻造前圆柱的体积=锻造后圆柱的体积
解:设锻造后圆柱高为x厘米,根据题意,得
解这个方程,得 x=36
答:锻造后圆柱的高为36厘米
20cm
9cm
10cm
cm
π×( ) ×9=π×( ) ×
新知讲解
讨 论
例2、小明将一个正方形纸剪出一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,如果两次剪下的长条面积正好相等,求正方形的边长
1、本题中有什么等量关系?
宽为4cm的长条面积=宽为5cm的长条面积
宽 长 面积
图形1
图形2
4
5
x
X-4
4x
5(x-4)
2、设正方形 的边长为xcm,完成下表
解:设正方形 的边长为xcm,由题意可得:
4x=5(x-4)
解这个方程,得 x=20
答:正方形的边长20cm。
新知讲解
①形状发生了变化,体积不变.其相等关系是:变化前图形的体积=变化后图形的体积.
②形状、面积发生了变化,周长不变.其相等关系是:变化前图形的周长=变化后图形的周长.
③形状、体积不同,面积相同.根据题意找出面积之间的关系,即为相等关系.
形积变化中的等量关系
形积变化问题中,图形的形状和体积会发生变化,应用题中相等关系可分以下几种情况:
新知讲解
例3、某居民楼顶有一个底面直径和高均为4m的圆柱形储水箱,现该楼进行维修改造,为减少楼顶原有储水箱的占地面积,需要将它的底面直径由4m减少为3.2m.那么在容积不变的前提下,水箱的高度将由原先的4m增高为多少米?
设维修后水箱的高为x米,填写下表:
旧水箱 新水箱
底面半径/m
高/m
体积/m3
等量关系:
维修前的体积=维修后的体积
新知讲解
解:设维修后水箱的高为x米,由题意可得:
解得
答:高变成了 米.
检查所得的值是否正确和符合实际情形,并写出答案(包括单位名称).
列一元一次方程解应用 题的一般步骤
新知总结
(1)审题设元:
弄清题意和题目中的数量关系,用字母(如x,y)表示问题中的未知数;
(2)找等量关系:
分析题意,找出相等关系(可借助于示意图、表格等);
(3)列方程:
根据相等关系,列出需要的代数式,并列出方程;
(4)解方程:
解这个方程,求出未知数的值;
(5)检验作答:
1、在应用方程解决问有关实际问题时,清楚地分辨量之间的关系,尤其相等关系是建立方程的关键。
2、解题中的检验对确保答案的正确和合理很有帮助,但具体过程可省略不写。
新知总结
注 意
1、 用一根长12cm的铁丝围成一个长方形,使得长方形的宽是长的一半,则这个长方形的面积是( )
A. 4cm2 B. 6cm2 C. 8cm2 D. 12cm2
课堂练习
C
2、一个长方形的周长为16cm,长与宽的差是1cm,那么长与宽分别为( )
A.5cm,3cm B.4.5cm,3.5cm
C.5cm,4cm D.8.5cm,7.5cm
B
3、根据图中给出的信息,可得正确的方程是( )
A.π×42x=π×32×(x+5) B.π×42x=π×32×(x-5)
C.π×82x=π×62×(x+5) D.π×82x=π×62×(x-5)
B
4、内直径为20 cm的圆柱形水桶中的全部水倒入一个长、宽、高分别为30 cm,20 cm,80 cm的长方形铁盒中,正好倒满,求圆柱形水桶的高.(π取3.14)
答:圆柱形水桶高约为152.87 cm.
解:设圆柱形水桶高x cm.根据题意,得
π · x= 30×20×80.
解得 x= ≈152.87.
课堂练习
60m
30m
30m
本题中有什么等量关系
5、 把一块梯形空地改成宽为30米的长方形运动场,要求面积不变,则应将原梯形的上、下底边作怎样的调整?
改造前的梯形的面积=改造后的长方形的面积
30m
解:设长方形的长为x米,根据题意,得
30x=(30+60)×30÷2
解这个方程,得 x=45
60-45=15(米)
45-30=15(米)
答:应将梯形的上底边缩短15米,下底边延长15米。
x
1、如图一个铁片长30cm,宽20cm,打算从四个角各截去一个小正方形,然后把四边折起来做一个无盖的铁盒,铁盒的底面周长为60cm,问铁盒的高是多少?
30cm
20cm
拓展提高
x
30-2x
20-2x
30-2x
20-2x
解:设铁盒的高是xcm,由题意可得:
[30-2x+(20-2x)]×2=60
解这个方程,得 x=5
答:铁盒的高是5cm
2、根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高 ,放入一个大球水面上升 ;
(2)如果要使水面上升到50cm,应放入大球________个,小球________个.
2cm
3cm
6
4
解:设小球放x个,大球则放(10-x)个,由题意得
3(10-x)+2x=50-26
解方程得 x=6
10-x=4
课堂小结
用一元一次方程解决实际问题的基本过程
实际问题
一元一次方程
设未知数,列方程
解方程
一元一次方程的解(x = a)
实际问题的答案
检 验
第3章 一次方程与方程组
第1课时 图形等积和变换问题
3.2 一元一次方程的应用
沪科版数学七年级上册
教学目标
【知识与技能】
1.通过分析图形问题中的基本等量关系,建立方程解决问题.
2.进一步了解一元一次方程在解决实际问题中的应用.
【过程与方法】
用实例对一些数学猜想做出检验,从而增加猜想的可信程度或推翻猜想.
【情感、态度与价值观】
培养学生敢于面对和克服数学活动中困难的能力,使他们拥有运用知识解决问题的成功体验,建立学好数学的自信心.
长方体的体积=长×宽×高;
正方体的体积=棱长×棱长×棱长;
圆柱体的体积=底面积×高=πr2h;
圆锥体的体积= ×底面积×高= πr2h.
知识回顾
常用的体积公式
新知导入
h
r
阿基米德为了帮助国王辨别皇冠的真假,需要测量皇冠的体积,确定皇冠的密度,聪明的阿基米德用非常巧妙地方法测出了皇冠的体积,你知道他是如何测量的吗?
=
形状改变,
体积不变。
在实验过程中,哪些量发生了变化,哪些量保持不变
皇冠的体积=上升水的体积
把一块长、宽、高分别为5cm、3cm、3cm的长方体铁块,浸入半径为4cm的圆柱形玻璃杯中(盛有水),水面将增高多少?(不外溢)
在实验过程中,哪些量发生了变化,哪些量保持不变
体积不变。
新知导入
铁块体积=上升水的体积
上升水的形状为圆柱
形状改变
铁块的形状是长方体
新知导入
请指出下列过程中,哪些量发生了变化,哪些量保持不变
(1)把一小杯水倒入另一只大杯中
(2)用一根15cm长的铁丝围成一个三角形,然后把它改围成长方形.
(3)用一块橡皮泥先做成一个立方体,再把它该做成球.
水的底面积和高度发生变化,水的体积和质量不变.
围成图形的面积发生变化,但铁丝长度不变.
形状发生改变,但体积不变。
例1、有一个底面直径是20cm,高9cm的圆柱,工人叔叔要把它锻造成底面直径是10cm的圆柱,工人叔叔想知道锻造后的圆柱有多少高?你能告诉他吗?
20cm
9cm
10cm
cm
新知讲解
2、根据这个等量关系怎样列方程?
1、本题中有什么等量关系?
锻造前圆柱的体积=锻造后圆柱的体积
解:设锻造后圆柱高为x厘米,根据题意,得
解这个方程,得 x=36
答:锻造后圆柱的高为36厘米
20cm
9cm
10cm
cm
π×( ) ×9=π×( ) ×
新知讲解
讨 论
例2、小明将一个正方形纸剪出一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,如果两次剪下的长条面积正好相等,求正方形的边长
1、本题中有什么等量关系?
宽为4cm的长条面积=宽为5cm的长条面积
宽 长 面积
图形1
图形2
4
5
x
X-4
4x
5(x-4)
2、设正方形 的边长为xcm,完成下表
解:设正方形 的边长为xcm,由题意可得:
4x=5(x-4)
解这个方程,得 x=20
答:正方形的边长20cm。
新知讲解
①形状发生了变化,体积不变.其相等关系是:变化前图形的体积=变化后图形的体积.
②形状、面积发生了变化,周长不变.其相等关系是:变化前图形的周长=变化后图形的周长.
③形状、体积不同,面积相同.根据题意找出面积之间的关系,即为相等关系.
形积变化中的等量关系
形积变化问题中,图形的形状和体积会发生变化,应用题中相等关系可分以下几种情况:
新知讲解
例3、某居民楼顶有一个底面直径和高均为4m的圆柱形储水箱,现该楼进行维修改造,为减少楼顶原有储水箱的占地面积,需要将它的底面直径由4m减少为3.2m.那么在容积不变的前提下,水箱的高度将由原先的4m增高为多少米?
设维修后水箱的高为x米,填写下表:
旧水箱 新水箱
底面半径/m
高/m
体积/m3
等量关系:
维修前的体积=维修后的体积
新知讲解
解:设维修后水箱的高为x米,由题意可得:
解得
答:高变成了 米.
检查所得的值是否正确和符合实际情形,并写出答案(包括单位名称).
列一元一次方程解应用 题的一般步骤
新知总结
(1)审题设元:
弄清题意和题目中的数量关系,用字母(如x,y)表示问题中的未知数;
(2)找等量关系:
分析题意,找出相等关系(可借助于示意图、表格等);
(3)列方程:
根据相等关系,列出需要的代数式,并列出方程;
(4)解方程:
解这个方程,求出未知数的值;
(5)检验作答:
1、在应用方程解决问有关实际问题时,清楚地分辨量之间的关系,尤其相等关系是建立方程的关键。
2、解题中的检验对确保答案的正确和合理很有帮助,但具体过程可省略不写。
新知总结
注 意
1、 用一根长12cm的铁丝围成一个长方形,使得长方形的宽是长的一半,则这个长方形的面积是( )
A. 4cm2 B. 6cm2 C. 8cm2 D. 12cm2
课堂练习
C
2、一个长方形的周长为16cm,长与宽的差是1cm,那么长与宽分别为( )
A.5cm,3cm B.4.5cm,3.5cm
C.5cm,4cm D.8.5cm,7.5cm
B
3、根据图中给出的信息,可得正确的方程是( )
A.π×42x=π×32×(x+5) B.π×42x=π×32×(x-5)
C.π×82x=π×62×(x+5) D.π×82x=π×62×(x-5)
B
4、内直径为20 cm的圆柱形水桶中的全部水倒入一个长、宽、高分别为30 cm,20 cm,80 cm的长方形铁盒中,正好倒满,求圆柱形水桶的高.(π取3.14)
答:圆柱形水桶高约为152.87 cm.
解:设圆柱形水桶高x cm.根据题意,得
π · x= 30×20×80.
解得 x= ≈152.87.
课堂练习
60m
30m
30m
本题中有什么等量关系
5、 把一块梯形空地改成宽为30米的长方形运动场,要求面积不变,则应将原梯形的上、下底边作怎样的调整?
改造前的梯形的面积=改造后的长方形的面积
30m
解:设长方形的长为x米,根据题意,得
30x=(30+60)×30÷2
解这个方程,得 x=45
60-45=15(米)
45-30=15(米)
答:应将梯形的上底边缩短15米,下底边延长15米。
x
1、如图一个铁片长30cm,宽20cm,打算从四个角各截去一个小正方形,然后把四边折起来做一个无盖的铁盒,铁盒的底面周长为60cm,问铁盒的高是多少?
30cm
20cm
拓展提高
x
30-2x
20-2x
30-2x
20-2x
解:设铁盒的高是xcm,由题意可得:
[30-2x+(20-2x)]×2=60
解这个方程,得 x=5
答:铁盒的高是5cm
2、根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高 ,放入一个大球水面上升 ;
(2)如果要使水面上升到50cm,应放入大球________个,小球________个.
2cm
3cm
6
4
解:设小球放x个,大球则放(10-x)个,由题意得
3(10-x)+2x=50-26
解方程得 x=6
10-x=4
课堂小结
用一元一次方程解决实际问题的基本过程
实际问题
一元一次方程
设未知数,列方程
解方程
一元一次方程的解(x = a)
实际问题的答案
检 验
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
