人教版高中数学选择性必修第一册2.2.3直线的一般式方程 课件(共30张PPT)
文档属性
| 名称 | 人教版高中数学选择性必修第一册2.2.3直线的一般式方程 课件(共30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 853.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-20 00:00:00 | ||
图片预览










文档简介
(共30张PPT)
2.2.3 直线的一般式方程
[学习目标]
1.明确直线方程一般式的形式特征.
2.会把直线方程的一般式化为斜截式,进而求斜率和截距.
3.会把直线方程的点斜式、两点式化为一般式.
必备知识 自主探究
关键能力 互动探究
课时作业 巩固提升
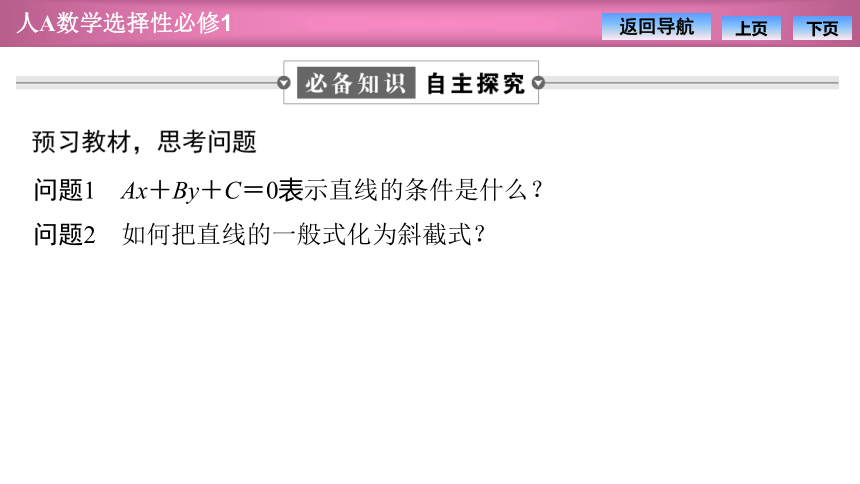
问题1 Ax+By+C=0表示直线的条件是什么?
问题2 如何把直线的一般式化为斜截式?
解析:由题意得3y+6=x-1,
整理得x-3y-7=0.
B
2.把直线的一般式方程x+y-1=0化为斜截式,正确的是( )
A.y=x-1
B.y=-x-1
C.y=-x+1
D.y=x+1
解析:移项得y=-x+1.
C
3.直线x+2y=0在y轴上的截距为__________.
解析:在直线的方程x+2y=0中,令x=0,得y=0,
即直线在y轴上的截距为0.
4.直线y=k(x-2)恒过一定点,则该定点坐标为__________.
解析:直线的点斜式方程为y-0=k(x-2),
故直线恒过定点(2,0).
0
(2,0)
直线的一般式方程
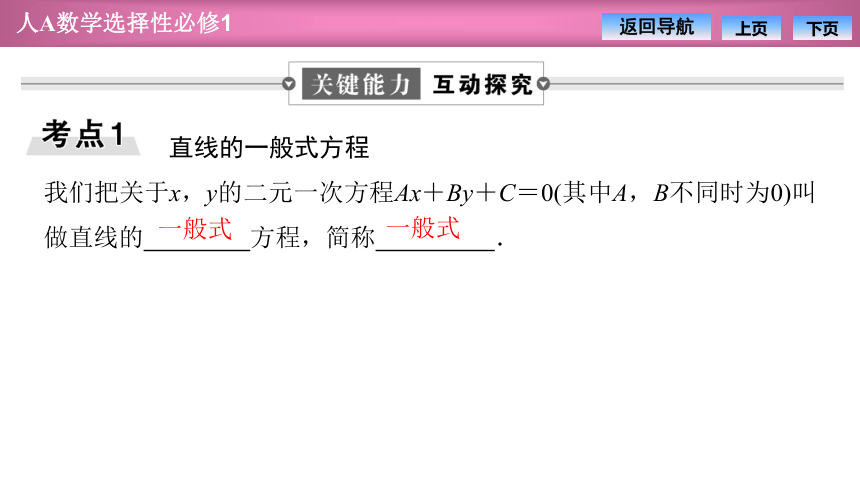
我们把关于x,y的二元一次方程Ax+By+C=0(其中A,B不同时为0)叫做直线的 方程,简称 .
一般式
一般式
[例1] 已知直线经过点(1,-1),斜率为2,求直线的点斜式方程,并化成一般式.
分析:将已知条件代入直线的点斜式方程y-y0=k(x-x0).
[解析] 由直线的点斜式方程可得y-(-1)=2(x-1),化成一般式为2x-y-3=0.
直线的一般式方程与其他形式方程的互化
直线的点斜式、斜截式、两点式和截距式方程四种形式之间的转化,一般要利用一般式方程作为桥梁,先将一种形式的方程化为一般式方程,然后将一般式方程转化为另一种形式.
1.把直线l的一般式方程2x-y+4=0化为斜截式,求出直线l的斜率以及它在x轴与y轴上的截距,并画出图形.
解析:把直线l的一般式方程化为斜截式y=2x+4.
因此,直线l的斜率k=2,它在y轴上的截距是4,
在直线l的方程2x-y+4=0中,令y=0,得x=-2,
即直线l在x轴上的截距是-2.
由上面可得直线l与x轴,y轴的交点分别为A(-2,0),B(0,4),过A,B两点作直线,就得直线l.
定点问题
直线y-y0=k(x-x0)恒过定点 .
[例2] 已知直线l:5ax-5y-a+3=0.
(1)求证:不论实数a为何值,直线l总经过第一象限;
(2)求使直线l不经过第二象限的a的取值范围.
分析:将直线l的一般式方程化为点斜式方程.
(x0,y0)
1.将方程化为点斜式y-y0=k(x-x0),其中k为参数,求得直线恒过定点(x0,y0).
2.分离参数法:将方程变形,把x,y作为参数的系数,即有参数的放在一起,没参数的放在一起,因为此式子对任意的参数的值都成立,故需系数为零,解方程组可得x,y的值,即为直线过的定点.
2.无论m取何实数,直线l:mx+y-1+2m=0恒过一定点,则该定点坐标为( )
A.(-2,1) B.(-2,-1)
C.(2,1) D.(2,-1)
A
2.点关于直线的对称问题
点P(x0,y0)关于直线Ax+By+C=0的对称点P′(x,y)满足:(1)线段PP′与直线垂直;(2)线段PP′的中点M在直线上,列两个方程然后求解.
点关于线对称的求解方法:设出对称点,利用垂直(当已知点与所求对称点连线斜率和已知直线斜率存在时,斜率之积为-1)、平分(点与对称点连线的中点在对称直线上)解决.
[例3] 如图,点A(4,0),B(0,4),点P(2,0)关于直线AB的对称点Q,点P关于y轴的对称点R,求直线QR的方程.
分析:先求出点P关于直线AB的对称点Q的坐标,再求点P关于y轴的对称点R的坐标,从而确定直线QR的方程.
点P(a,b)关于直线Ax+By+C=0对称点的求法:设出对称点Q(x,y),利用直线PQ与已知直线垂直,及PQ的中点在已知直线上列出方程组解决.
3.将一张坐标纸折叠一次,使得点(0,2)与点(4,0)重合,点(7,3)与点(m,n)重合,则m+n的值为( )
C
1.知识清单:(1)直线的一般式方程.
(2)直线方程几种形式的互化.
(3)过定点的直线.
(4)点关于点的对称.
(5)点关于直线的对称.
2.方法归纳:转化与化归、数形结合、分离参数法.
课时作业 巩固提升
2.2.3 直线的一般式方程
[学习目标]
1.明确直线方程一般式的形式特征.
2.会把直线方程的一般式化为斜截式,进而求斜率和截距.
3.会把直线方程的点斜式、两点式化为一般式.
必备知识 自主探究
关键能力 互动探究
课时作业 巩固提升
问题1 Ax+By+C=0表示直线的条件是什么?
问题2 如何把直线的一般式化为斜截式?
解析:由题意得3y+6=x-1,
整理得x-3y-7=0.
B
2.把直线的一般式方程x+y-1=0化为斜截式,正确的是( )
A.y=x-1
B.y=-x-1
C.y=-x+1
D.y=x+1
解析:移项得y=-x+1.
C
3.直线x+2y=0在y轴上的截距为__________.
解析:在直线的方程x+2y=0中,令x=0,得y=0,
即直线在y轴上的截距为0.
4.直线y=k(x-2)恒过一定点,则该定点坐标为__________.
解析:直线的点斜式方程为y-0=k(x-2),
故直线恒过定点(2,0).
0
(2,0)
直线的一般式方程
我们把关于x,y的二元一次方程Ax+By+C=0(其中A,B不同时为0)叫做直线的 方程,简称 .
一般式
一般式
[例1] 已知直线经过点(1,-1),斜率为2,求直线的点斜式方程,并化成一般式.
分析:将已知条件代入直线的点斜式方程y-y0=k(x-x0).
[解析] 由直线的点斜式方程可得y-(-1)=2(x-1),化成一般式为2x-y-3=0.
直线的一般式方程与其他形式方程的互化
直线的点斜式、斜截式、两点式和截距式方程四种形式之间的转化,一般要利用一般式方程作为桥梁,先将一种形式的方程化为一般式方程,然后将一般式方程转化为另一种形式.
1.把直线l的一般式方程2x-y+4=0化为斜截式,求出直线l的斜率以及它在x轴与y轴上的截距,并画出图形.
解析:把直线l的一般式方程化为斜截式y=2x+4.
因此,直线l的斜率k=2,它在y轴上的截距是4,
在直线l的方程2x-y+4=0中,令y=0,得x=-2,
即直线l在x轴上的截距是-2.
由上面可得直线l与x轴,y轴的交点分别为A(-2,0),B(0,4),过A,B两点作直线,就得直线l.
定点问题
直线y-y0=k(x-x0)恒过定点 .
[例2] 已知直线l:5ax-5y-a+3=0.
(1)求证:不论实数a为何值,直线l总经过第一象限;
(2)求使直线l不经过第二象限的a的取值范围.
分析:将直线l的一般式方程化为点斜式方程.
(x0,y0)
1.将方程化为点斜式y-y0=k(x-x0),其中k为参数,求得直线恒过定点(x0,y0).
2.分离参数法:将方程变形,把x,y作为参数的系数,即有参数的放在一起,没参数的放在一起,因为此式子对任意的参数的值都成立,故需系数为零,解方程组可得x,y的值,即为直线过的定点.
2.无论m取何实数,直线l:mx+y-1+2m=0恒过一定点,则该定点坐标为( )
A.(-2,1) B.(-2,-1)
C.(2,1) D.(2,-1)
A
2.点关于直线的对称问题
点P(x0,y0)关于直线Ax+By+C=0的对称点P′(x,y)满足:(1)线段PP′与直线垂直;(2)线段PP′的中点M在直线上,列两个方程然后求解.
点关于线对称的求解方法:设出对称点,利用垂直(当已知点与所求对称点连线斜率和已知直线斜率存在时,斜率之积为-1)、平分(点与对称点连线的中点在对称直线上)解决.
[例3] 如图,点A(4,0),B(0,4),点P(2,0)关于直线AB的对称点Q,点P关于y轴的对称点R,求直线QR的方程.
分析:先求出点P关于直线AB的对称点Q的坐标,再求点P关于y轴的对称点R的坐标,从而确定直线QR的方程.
点P(a,b)关于直线Ax+By+C=0对称点的求法:设出对称点Q(x,y),利用直线PQ与已知直线垂直,及PQ的中点在已知直线上列出方程组解决.
3.将一张坐标纸折叠一次,使得点(0,2)与点(4,0)重合,点(7,3)与点(m,n)重合,则m+n的值为( )
C
1.知识清单:(1)直线的一般式方程.
(2)直线方程几种形式的互化.
(3)过定点的直线.
(4)点关于点的对称.
(5)点关于直线的对称.
2.方法归纳:转化与化归、数形结合、分离参数法.
课时作业 巩固提升
