人教版数学八年级上册 15.2.2 分式的加减 课件(共25张PPT)
文档属性
| 名称 | 人教版数学八年级上册 15.2.2 分式的加减 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 09:30:12 | ||
图片预览







文档简介
(共25张PPT)
15.2 分式的运算
15.2.2 分式的加减
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
问题1 甲工程队完成一项工程需要n天,乙工程队要比甲队多3天才能完成这项工程,两队共同工作一天完成这项工程的几分之几?
解: 甲工程队一天完成这项工程的________ ,
乙工程队一天完成这项工程的 ________ ,
两队共同工作一天完成这项工程的:
新课导入
解:2011年的森林面积增长率是:________;
2010年的森林面积增长率是:_________;
2011年与2010年相比,森林面积增长率提高了:
问题2 2009年,2010年,2011年某地的森林面积(单位:km2)分别是S1 , S2 , S3 ,2011年与2010年相比,森林面积的增长率提高了多少?
新课导入
讲授新知
贰
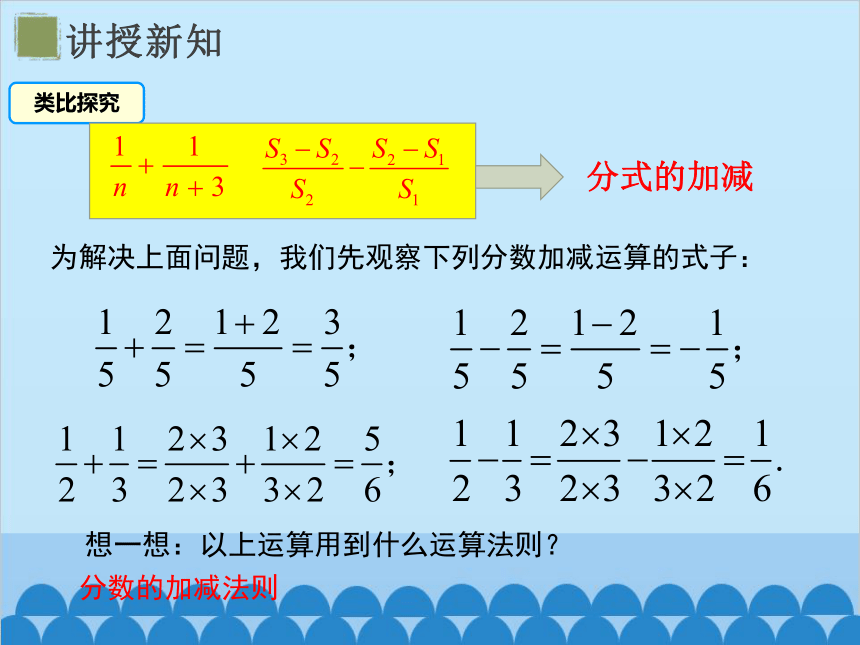
类比探究
为解决上面问题,我们先观察下列分数加减运算的式子:
想一想:以上运算用到什么运算法则?
分数的加减法则
分式的加减
讲授新知
用式子表示:
同分母分式的加减法法则:同分母分式相加减,分母不变,把分子相加减.
(1)同分母分式相加减时,“把分子相加减”就是把各个分式的分子“整体”相加减.
(2)在计算时,各分子都应用括号括起来,若分子是系数为正的单项式,括号可以省略;若分子是多项式,且分子相减时,括号不能省略,否则容易出现符号错误.
知识点1 同分母分式的加减法则
讲授新知
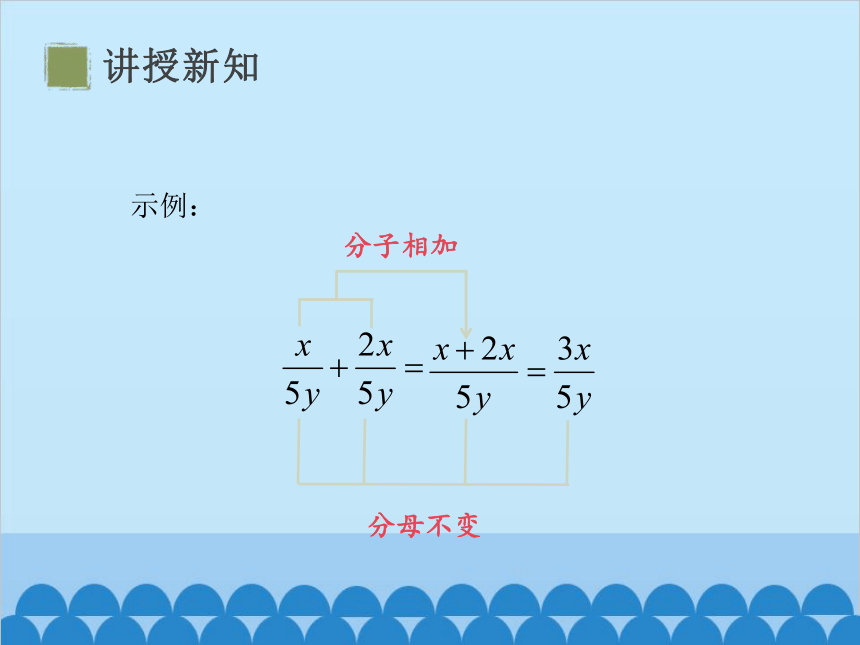
示例:
分母不变
分子相加
讲授新知
示例:
异分母
同分母
通分
知识点2 异分母分式的加减法则
异分母分式的加减法法则:异分母分式相加减,先通分,变为同分母的分式,再加减.
用式子表示:
讲授新知
例1 计算:
⑴
⑵
解:⑴原式
计算前先观察分母,看是否需要通分。
结果要化为最简!
范例应用
⑵原式
先通分,化为同分母
整理结果,化为最简
范例应用
情境问题现在迎刃而解
问题1
即2011年与2010年相比,森林面积增长率提高了
问题2
范例应用
(1)先算乘方,再算乘除,最后算加减,有括号的先算括号里面的,在没有括号的情况下,按从左往右的方向;
(2)分式的混合运算,一般按常规运算顺序,但有时应先根据题目的特点,运用乘法的运算律进行灵活运算.
知识点3 分式的混合运算
分式的混合运算中要注意各分式中分子、分母符号的处理,结果中分子或分母的系数(或首项的系数)是负数时,要把“-”号提到分式本身的前面.
讲授新知
解:
先乘方,再乘除,然后加减
例2 计算
范例应用
例3 计算
解:
出现整式时,把整式看成整体,并把分母看做“1”.
范例应用
解:
注意:分子或分母是多项式的先因式分解,不能分解的要视为整体
范例应用
当堂训练
叁
A. B. C.-1 D.2
1. 计算
的结果为( )
C
2.填空:
(3) 的最简公分母是 .
4
12x
当堂训练
3. 计算 的结果是( )
A.
B.
C.
D.
4. 化简 的结果是 .
5. 化简 的结果是 .
C
当堂训练
(3)原式
(3)
(2)原式=
解:(1)原式=
6.计算:
当堂训练
课堂小结
肆
课堂小结
分式的运算
混合运算
同分母分式的加减法法则
异分母分式的加减法法则
1.同级运算自左向右进行;
2.运算律可简化运算
课后作业
基础题:1.P141课后练习1,2;P142课后练习2.
提高题:2.请学有余力的同学完成同步训练本课时的习题。
谢
谢
15.2 分式的运算
15.2.2 分式的加减
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
问题1 甲工程队完成一项工程需要n天,乙工程队要比甲队多3天才能完成这项工程,两队共同工作一天完成这项工程的几分之几?
解: 甲工程队一天完成这项工程的________ ,
乙工程队一天完成这项工程的 ________ ,
两队共同工作一天完成这项工程的:
新课导入
解:2011年的森林面积增长率是:________;
2010年的森林面积增长率是:_________;
2011年与2010年相比,森林面积增长率提高了:
问题2 2009年,2010年,2011年某地的森林面积(单位:km2)分别是S1 , S2 , S3 ,2011年与2010年相比,森林面积的增长率提高了多少?
新课导入
讲授新知
贰
类比探究
为解决上面问题,我们先观察下列分数加减运算的式子:
想一想:以上运算用到什么运算法则?
分数的加减法则
分式的加减
讲授新知
用式子表示:
同分母分式的加减法法则:同分母分式相加减,分母不变,把分子相加减.
(1)同分母分式相加减时,“把分子相加减”就是把各个分式的分子“整体”相加减.
(2)在计算时,各分子都应用括号括起来,若分子是系数为正的单项式,括号可以省略;若分子是多项式,且分子相减时,括号不能省略,否则容易出现符号错误.
知识点1 同分母分式的加减法则
讲授新知
示例:
分母不变
分子相加
讲授新知
示例:
异分母
同分母
通分
知识点2 异分母分式的加减法则
异分母分式的加减法法则:异分母分式相加减,先通分,变为同分母的分式,再加减.
用式子表示:
讲授新知
例1 计算:
⑴
⑵
解:⑴原式
计算前先观察分母,看是否需要通分。
结果要化为最简!
范例应用
⑵原式
先通分,化为同分母
整理结果,化为最简
范例应用
情境问题现在迎刃而解
问题1
即2011年与2010年相比,森林面积增长率提高了
问题2
范例应用
(1)先算乘方,再算乘除,最后算加减,有括号的先算括号里面的,在没有括号的情况下,按从左往右的方向;
(2)分式的混合运算,一般按常规运算顺序,但有时应先根据题目的特点,运用乘法的运算律进行灵活运算.
知识点3 分式的混合运算
分式的混合运算中要注意各分式中分子、分母符号的处理,结果中分子或分母的系数(或首项的系数)是负数时,要把“-”号提到分式本身的前面.
讲授新知
解:
先乘方,再乘除,然后加减
例2 计算
范例应用
例3 计算
解:
出现整式时,把整式看成整体,并把分母看做“1”.
范例应用
解:
注意:分子或分母是多项式的先因式分解,不能分解的要视为整体
范例应用
当堂训练
叁
A. B. C.-1 D.2
1. 计算
的结果为( )
C
2.填空:
(3) 的最简公分母是 .
4
12x
当堂训练
3. 计算 的结果是( )
A.
B.
C.
D.
4. 化简 的结果是 .
5. 化简 的结果是 .
C
当堂训练
(3)原式
(3)
(2)原式=
解:(1)原式=
6.计算:
当堂训练
课堂小结
肆
课堂小结
分式的运算
混合运算
同分母分式的加减法法则
异分母分式的加减法法则
1.同级运算自左向右进行;
2.运算律可简化运算
课后作业
基础题:1.P141课后练习1,2;P142课后练习2.
提高题:2.请学有余力的同学完成同步训练本课时的习题。
谢
谢
