山西省大同市阳高县第一中学校2022-2023学年高二下学期7月期末考试数学试题(Word版含答案)
文档属性
| 名称 | 山西省大同市阳高县第一中学校2022-2023学年高二下学期7月期末考试数学试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 539.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-20 17:57:01 | ||
图片预览




文档简介
阳高县第一中学校2022-2023学年高二下学期7月期末考试
数学试题
姓名___________班级___________考号___________
一、选择题(本大题共12道小题,每小题5分,共计60分。在每小题给出的四个选项中,只有一项是符合题目要求的.)
1、已知集合,,则( )
A. B. C. D.
2、设,则“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
3、若函数y=的定义域为R,则实数a的取值范围是( )
A. B. C. D.
4、青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L和小数记录表的数据V的满足.已知某同学视力的五分记录法的数据为4.9,则其视力的小数记录法的数据为()( )
A.1.5 B.1.2 C.0.8 D.0.6
5、下列各组函数中,表示同一函数的是( )
A.与 B.与
C.与 D.与
6、已知复数z满足,则( )
A. B. C. D.
7、“圆柱容球”是指圆柱形容器里放了一个球,且球与圆柱的侧面及上、下底面均相切,则该圆柱的体积与球的体积之比为( )
A. 2 B. C. D.
8、“”是“”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
9、新能源汽车的核心部件是动力电池,碳酸锂是动力电池的主要成分.从2021年底开始,碳酸锂的价格一直升高,下表是2022年我国某企业前5个月购买碳酸锂价格与月份的统计数据.由下表可知其线性回归方程为,则表中的值为( )
月份代码 1 2 3 4 5
碳酸锂价格(万元/) 0.5 1 1.4 1.5
A. 0.5 B. 0.6 C. 0.7 D. 0.8
10、展开式中的系数为( )
A. 200 B. 210 C. 220 D. 230
11、导函数的图象如图所示,下列说法正确的个数是( )
①导函数在处有极小值
②函数在处有极大值
③函数在上是减函数
④函数在是增函数
A. 1 B. 2 C. 3 D. 4
12、在中,点是线段上任意一点(不包含端点),若,则的最小值是( )
A.4 B.9 C.8 D.13
二、填空题(本大题共4小题,每小题5分,共20分)
13、函数,的值域是__________.
14、定义在R上的奇函数满足是偶函数,且当时,,则__________.
15、如图,在中,M为AB的中点,点O满足,,若,则______.
16、假设云南省40万学生数学模拟考试的成绩近似服从正态分布,已知某学生成绩排名进入全省前9100名,那么该生的数学成绩不会低于____________分.(参考数据:,)
三、解答题(本大题共6小题,第17题10分,其余每题12分,共70分)
17、如图是某企业2016年至2022年的污水净化量(单位:吨)的折线图.
注:年份代码1~7分别对应年份2016~2022.
(1)由折线图看出,可用线性回归模型拟合y和t的关系,请建立y关于t的回归方程,并预测2025年该企业的污水净化量;
(2)请用相关指数说明回归方程预报的效果.
参考数据:;
参考公式:线性回归方程,;相关指数:
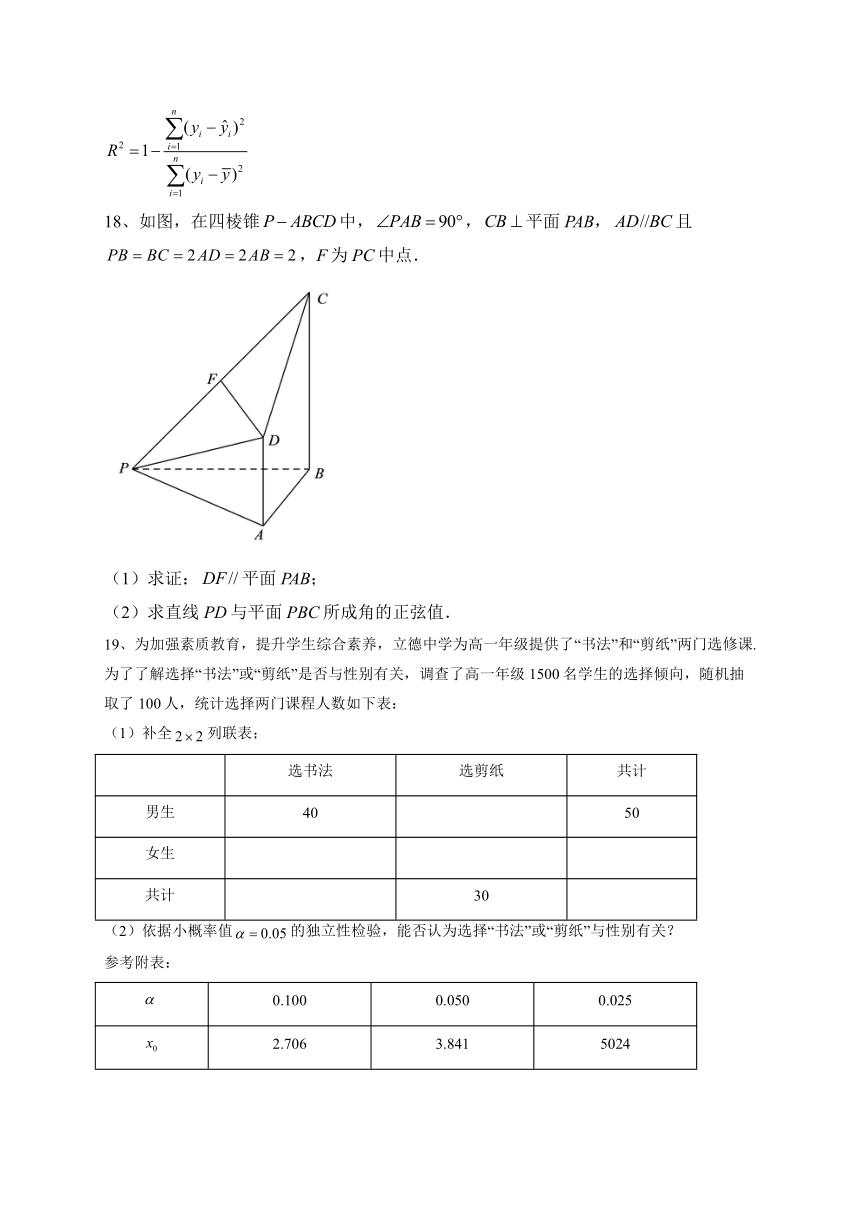
18、如图,在四棱锥中,,平面PAB,且,F为PC中点.
(1)求证:平面PAB;
(2)求直线PD与平面PBC所成角的正弦值.
19、为加强素质教育,提升学生综合素养,立德中学为高一年级提供了“书法”和“剪纸”两门选修课.为了了解选择“书法”或“剪纸”是否与性别有关,调查了高一年级1500名学生的选择倾向,随机抽取了100人,统计选择两门课程人数如下表:
(1)补全列联表;
选书法 选剪纸 共计
男生 40 50
女生
共计 30
(2)依据小概率值的独立性检验,能否认为选择“书法”或“剪纸”与性别有关?
参考附表:
0.100 0.050 0.025
2.706 3.841 5024
参考公式:,其中.
20、设某工厂有甲、乙、丙三个车间,它们生产同一种工件,每个车间的产量占该厂总产量的百分比依次为25%,35%,40%,它们的次品率依次为5%,4%,2%.现从这批工件中任取一件.
(1)求取到次品的概率;
(2)已知取到的是次品,求它是甲车间生产的概率.(精确到0.01)
21、已知函数(),().
(1)讨论函数的单调性;
(2)当时,函数、满足下面两个条件:① 方程有唯一实数解;② 直线()与两条曲线和有四个不同的交点,从左到右依次为,,,.问是否存在1,2,3,4的一个排列,使得?如果存在,请给出证明;如果不存在,说明理由.
22、已知函数,当时,,当时,.
(1)求的解析式;
(2)若不等式的解集为R,求c的取值范围;
(3)当时,求的最大值.
参考答案
一、选择题(本大题共12道小题,每小题5分,共计60分。在每小题给出的四个选项中,只有一项是符合题目要求的.)
1、C 2、B 3、D4、C 5、B 6、C 7、B 8、B 9、B 10、A 11、B 12、B
二、填空题(本大题共4小题,每小题5分,共20分)
13、答案: 14、答案:-1
15、答案:2 16、答案:118
三、解答题(本大题共6小题,第17题10分,其余每题12分,共70分)
17、答案:(1),58.5吨
(2)答案见解析
解析:(1)由折线图中的数据得,,
,
所以,
所以y关于t的线性回归方程为,
将2025年对应的代入得,
所以预测2025年该企业污水净化量约为58.5吨.
(2)因为,
所以“污水净化量的差异”有87.5%是由年份引起的,说明回归方程预报的效果是良好的.
18、答案: (1)证明见解析
(2)
解析:(1)证明:如图,取PB边的中点E,连接AE,FE,
则三角形中位线可知,且,
由题可知,且,所以且,
所以四边形AEFD为平行四边形,所以,
又因为平面PAB,平面PAB,
故平面PAB;
(2)过点A作于点N,
因为平面PAB,平面PAB,
所以,因,所以平面,
又,所以到平面的距离即为AN,
又,,
所以直线PD与平面PBC所成角为,所以;
19、答案:(1)见解析(2)有95%
解析:(1)根据题意补全列联表,如下:
选书法 选剪纸 共计
男生 40 10 50
女生 30 20 50
共计 70 30 100
(2)零假设为:选择“书法”或“剪纸”与性别无关.
根据列联表中数据,得,
根据小概率的独立性检验,推断不成立,即有95%的把握认为选“书法”或“剪纸”与性别有关.
20、答案:(1)0.0345(2)0.36
解析:(1)设事件,,分别表示取出的工件是甲、乙、丙车间生产的,A表示“取到的是次品.
易知,,两两互斥,根据全概率公式,
可得.
故取到次品的概率为0.0345.
(2).
故已知取到的是次品,它是甲车间生产的概率为0.36.
21、答案:(1)当时,,函数在上单调递减;
当时,对于,,函数单调递减;,,函数单调递增;
(2)见解析
解析:(1)由题可知,,
当时,,函数在上单调递减;
当时,对于,,函数单调递减;,,函数单调递增;
(2)由,,当时,;当时,,
又因为,所以在上单调递减,在上单调递增,;
由,知当时,;当,,
又,可知在上单调递减,在上单调递增,,
令,即当时,;当时,,
结合条件①中方程有唯一实数解,知:
当时,,当时,,
综上,画出函数,的简图:
其中,,,,,
则,,
即,得,,
因为,由,,得,
因为,由,,因此,
所以,,
所以存在满足条件的一个排列,如,,,,使.
22、答案:(1) (2) (3)
解析:(1)由已知得,方程的两个根为,2,
则,即解得,,
.
(2)由(1)得,不等式的解集为R,
因为,,
即c的取值范围为
(3),
因为,,
当且仅当,即时取等号,
∴当时,.
数学试题
姓名___________班级___________考号___________
一、选择题(本大题共12道小题,每小题5分,共计60分。在每小题给出的四个选项中,只有一项是符合题目要求的.)
1、已知集合,,则( )
A. B. C. D.
2、设,则“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
3、若函数y=的定义域为R,则实数a的取值范围是( )
A. B. C. D.
4、青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L和小数记录表的数据V的满足.已知某同学视力的五分记录法的数据为4.9,则其视力的小数记录法的数据为()( )
A.1.5 B.1.2 C.0.8 D.0.6
5、下列各组函数中,表示同一函数的是( )
A.与 B.与
C.与 D.与
6、已知复数z满足,则( )
A. B. C. D.
7、“圆柱容球”是指圆柱形容器里放了一个球,且球与圆柱的侧面及上、下底面均相切,则该圆柱的体积与球的体积之比为( )
A. 2 B. C. D.
8、“”是“”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
9、新能源汽车的核心部件是动力电池,碳酸锂是动力电池的主要成分.从2021年底开始,碳酸锂的价格一直升高,下表是2022年我国某企业前5个月购买碳酸锂价格与月份的统计数据.由下表可知其线性回归方程为,则表中的值为( )
月份代码 1 2 3 4 5
碳酸锂价格(万元/) 0.5 1 1.4 1.5
A. 0.5 B. 0.6 C. 0.7 D. 0.8
10、展开式中的系数为( )
A. 200 B. 210 C. 220 D. 230
11、导函数的图象如图所示,下列说法正确的个数是( )
①导函数在处有极小值
②函数在处有极大值
③函数在上是减函数
④函数在是增函数
A. 1 B. 2 C. 3 D. 4
12、在中,点是线段上任意一点(不包含端点),若,则的最小值是( )
A.4 B.9 C.8 D.13
二、填空题(本大题共4小题,每小题5分,共20分)
13、函数,的值域是__________.
14、定义在R上的奇函数满足是偶函数,且当时,,则__________.
15、如图,在中,M为AB的中点,点O满足,,若,则______.
16、假设云南省40万学生数学模拟考试的成绩近似服从正态分布,已知某学生成绩排名进入全省前9100名,那么该生的数学成绩不会低于____________分.(参考数据:,)
三、解答题(本大题共6小题,第17题10分,其余每题12分,共70分)
17、如图是某企业2016年至2022年的污水净化量(单位:吨)的折线图.
注:年份代码1~7分别对应年份2016~2022.
(1)由折线图看出,可用线性回归模型拟合y和t的关系,请建立y关于t的回归方程,并预测2025年该企业的污水净化量;
(2)请用相关指数说明回归方程预报的效果.
参考数据:;
参考公式:线性回归方程,;相关指数:
18、如图,在四棱锥中,,平面PAB,且,F为PC中点.
(1)求证:平面PAB;
(2)求直线PD与平面PBC所成角的正弦值.
19、为加强素质教育,提升学生综合素养,立德中学为高一年级提供了“书法”和“剪纸”两门选修课.为了了解选择“书法”或“剪纸”是否与性别有关,调查了高一年级1500名学生的选择倾向,随机抽取了100人,统计选择两门课程人数如下表:
(1)补全列联表;
选书法 选剪纸 共计
男生 40 50
女生
共计 30
(2)依据小概率值的独立性检验,能否认为选择“书法”或“剪纸”与性别有关?
参考附表:
0.100 0.050 0.025
2.706 3.841 5024
参考公式:,其中.
20、设某工厂有甲、乙、丙三个车间,它们生产同一种工件,每个车间的产量占该厂总产量的百分比依次为25%,35%,40%,它们的次品率依次为5%,4%,2%.现从这批工件中任取一件.
(1)求取到次品的概率;
(2)已知取到的是次品,求它是甲车间生产的概率.(精确到0.01)
21、已知函数(),().
(1)讨论函数的单调性;
(2)当时,函数、满足下面两个条件:① 方程有唯一实数解;② 直线()与两条曲线和有四个不同的交点,从左到右依次为,,,.问是否存在1,2,3,4的一个排列,使得?如果存在,请给出证明;如果不存在,说明理由.
22、已知函数,当时,,当时,.
(1)求的解析式;
(2)若不等式的解集为R,求c的取值范围;
(3)当时,求的最大值.
参考答案
一、选择题(本大题共12道小题,每小题5分,共计60分。在每小题给出的四个选项中,只有一项是符合题目要求的.)
1、C 2、B 3、D4、C 5、B 6、C 7、B 8、B 9、B 10、A 11、B 12、B
二、填空题(本大题共4小题,每小题5分,共20分)
13、答案: 14、答案:-1
15、答案:2 16、答案:118
三、解答题(本大题共6小题,第17题10分,其余每题12分,共70分)
17、答案:(1),58.5吨
(2)答案见解析
解析:(1)由折线图中的数据得,,
,
所以,
所以y关于t的线性回归方程为,
将2025年对应的代入得,
所以预测2025年该企业污水净化量约为58.5吨.
(2)因为,
所以“污水净化量的差异”有87.5%是由年份引起的,说明回归方程预报的效果是良好的.
18、答案: (1)证明见解析
(2)
解析:(1)证明:如图,取PB边的中点E,连接AE,FE,
则三角形中位线可知,且,
由题可知,且,所以且,
所以四边形AEFD为平行四边形,所以,
又因为平面PAB,平面PAB,
故平面PAB;
(2)过点A作于点N,
因为平面PAB,平面PAB,
所以,因,所以平面,
又,所以到平面的距离即为AN,
又,,
所以直线PD与平面PBC所成角为,所以;
19、答案:(1)见解析(2)有95%
解析:(1)根据题意补全列联表,如下:
选书法 选剪纸 共计
男生 40 10 50
女生 30 20 50
共计 70 30 100
(2)零假设为:选择“书法”或“剪纸”与性别无关.
根据列联表中数据,得,
根据小概率的独立性检验,推断不成立,即有95%的把握认为选“书法”或“剪纸”与性别有关.
20、答案:(1)0.0345(2)0.36
解析:(1)设事件,,分别表示取出的工件是甲、乙、丙车间生产的,A表示“取到的是次品.
易知,,两两互斥,根据全概率公式,
可得.
故取到次品的概率为0.0345.
(2).
故已知取到的是次品,它是甲车间生产的概率为0.36.
21、答案:(1)当时,,函数在上单调递减;
当时,对于,,函数单调递减;,,函数单调递增;
(2)见解析
解析:(1)由题可知,,
当时,,函数在上单调递减;
当时,对于,,函数单调递减;,,函数单调递增;
(2)由,,当时,;当时,,
又因为,所以在上单调递减,在上单调递增,;
由,知当时,;当,,
又,可知在上单调递减,在上单调递增,,
令,即当时,;当时,,
结合条件①中方程有唯一实数解,知:
当时,,当时,,
综上,画出函数,的简图:
其中,,,,,
则,,
即,得,,
因为,由,,得,
因为,由,,因此,
所以,,
所以存在满足条件的一个排列,如,,,,使.
22、答案:(1) (2) (3)
解析:(1)由已知得,方程的两个根为,2,
则,即解得,,
.
(2)由(1)得,不等式的解集为R,
因为,,
即c的取值范围为
(3),
因为,,
当且仅当,即时取等号,
∴当时,.
同课章节目录
