函数及其图像的复习[下学期]
图片预览






文档简介
课件31张PPT。第十八章 函数及其图象§18.3一次函数§18.4反比例函数§18.2函数的图象§18.2.2函数的图象§18.3.1一次函数§18.3.2一次函数的图象§18.3.3一次函数的性质§18.4.1反比例函数§18.4.2反比例函数的图象和性质§18.2.1平面直角坐标系在S=40t中,s随着t的变化而变化,这样的量叫变量, 象40这样不变量的叫常量。在某一变化过程中,可以取不同数值的量,叫做变量. 取值始终保持不变的量,称之为常量.一辆汽车以40千米/小时的速度行驶,
写出行驶路程s(千米)与行驶时间t(时)
的关系式。 S=40t1、变量和常量的概念一般地,在一个变化过程中有两个变量,例如x和y,如果对于x的每一个值,y都有唯一的值与之对应,我们就说是x是自变量, y是因变量,也把y叫做x的函数.当x取某一具体值时,y的值就叫做对应于x的函数值。自变量:是指在它的取值范围内可以随心所欲的、
自由自在的取它能取的值,看这概念够贴切了吧?
因变量:这个“因”字是指因x的变化,通过一定的
关系而得到的。2、函数的概念3、函数关系的三种表示方法:解析法、列表法、图象法 课内练习:1.求下列函数中自变量x的取值范围 (1)y = ; (2)y = x2-3x-2;
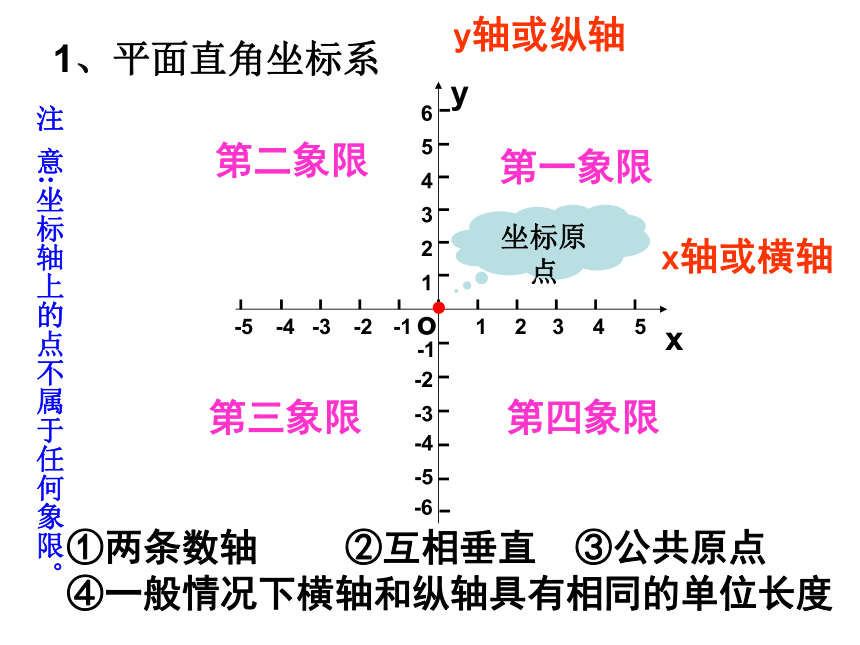
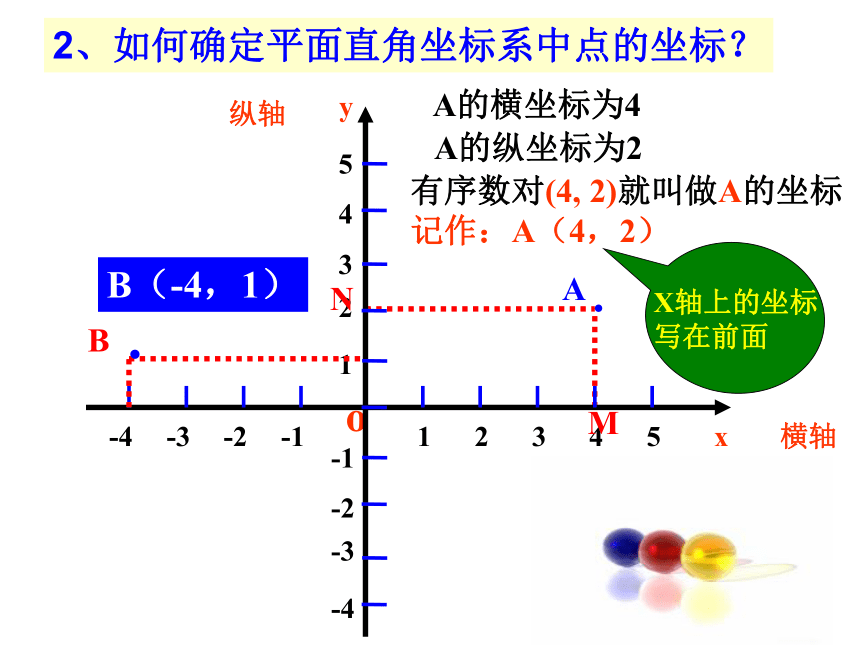
(3)y = ;(4)y = 2.某小汽车的油箱可装油30 L,每升汽油2.8元,该小汽车原有汽油10 L,现再加汽油x L,求油箱内汽油的总价值y(元)与x(L)之间的函数关系式,并写出自变量的取值范围.x轴或横轴y轴或纵轴坐标原点①两条数轴 ②互相垂直 ③公共原点 ④一般情况下横轴和纵轴具有相同的单位长度 第一象限第二象限第三象限第四象限注 意:坐标轴上的点不属于任何象限。1、平面直角坐标系·AA的横坐标为4A的纵坐标为2有序数对(4, 2)就叫做A的坐标
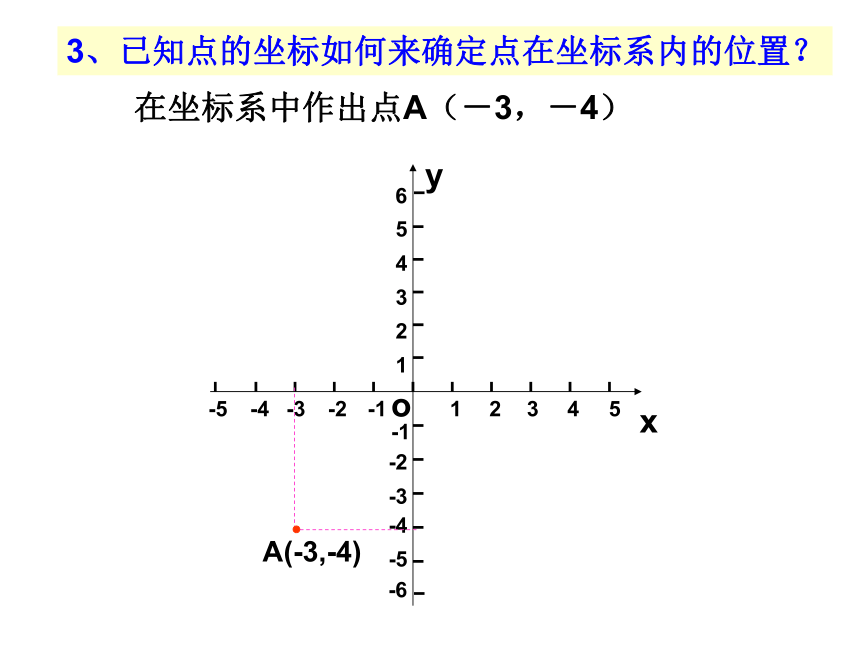
记作:A(4,2)B(-4,1)MN2、如何确定平面直角坐标系中点的坐标?A(-3,-4)3、已知点的坐标如何来确定点在坐标系内的位置?在坐标系中作出点A(-3,-4)1、能够正确画出直角坐标系。
2、能在直角坐标系中,根据坐标作出点,
由点求出坐标。
3、掌握各象限上及x轴,y轴上点的坐标的
特点:
第一象限(+,+) 第二象限(-,+)
第三象限(-,-)第四象限(+,-)
x轴上的点纵坐标为0,表示为(x,0)
y轴上的点横坐标为0,表示为(0,y)平面直角坐标系4、平行于横轴的直线上的点的纵坐标相同;
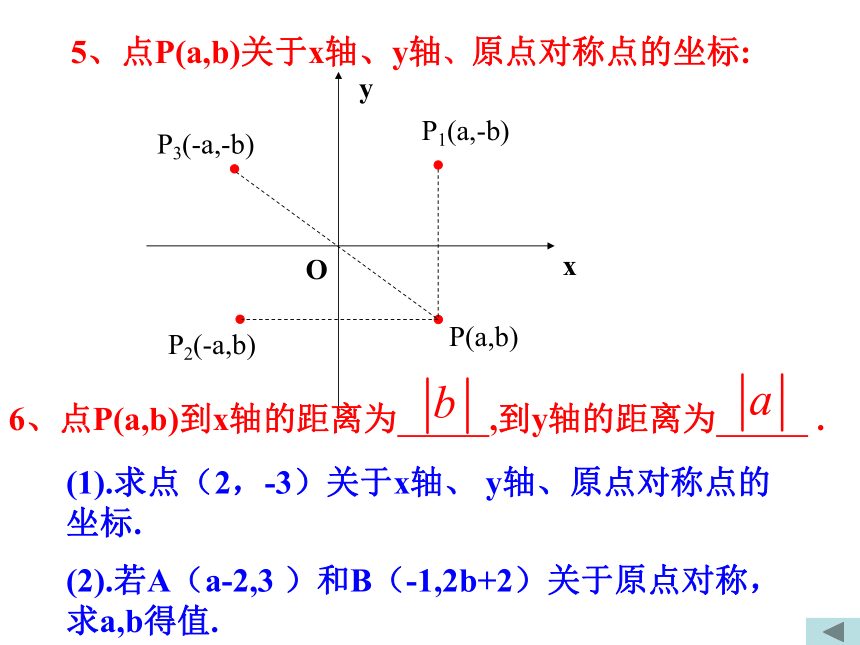
平行于纵轴的直线上的点的横坐标相同;P3(-a,-b)P(a,b)5、点P(a,b)关于x轴、y轴、原点对称点的坐标:P1(a,-b)P2(-a,b)6、点P(a,b)到x轴的距离为 ,到y轴的距离为 .(1).求点(2,-3)关于x轴、 y轴、原点对称点的坐标.
(2).若A(a-2,3 )和B(-1,2b+2)关于原点对称,
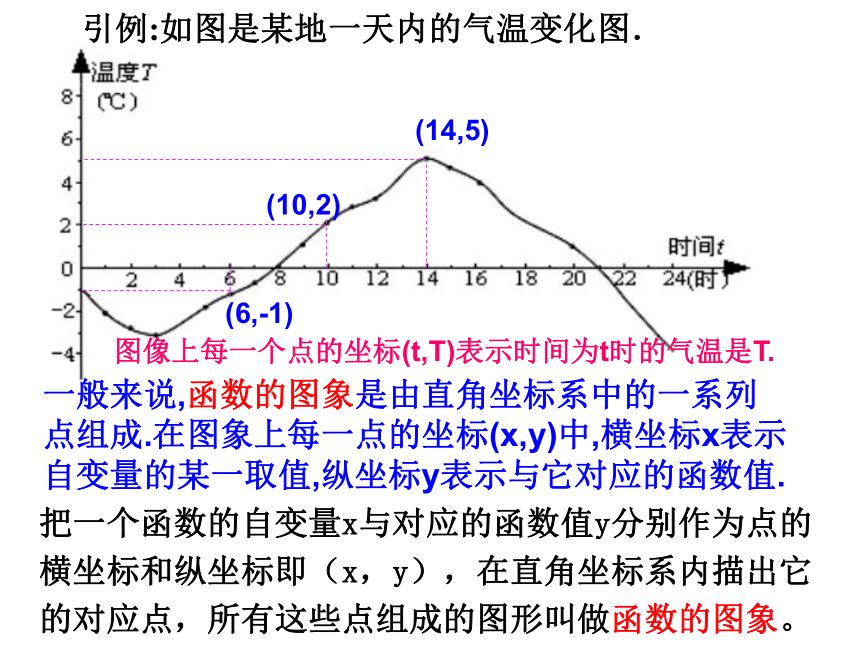
求a,b得值. 引例:如图是某地一天内的气温变化图.(6,-1)(10,2)(14,5)图像上每一个点的坐标(t,T)表示时间为t时的气温是T.一般来说,函数的图象是由直角坐标系中的一系列
点组成.在图象上每一点的坐标(x,y)中,横坐标x表示
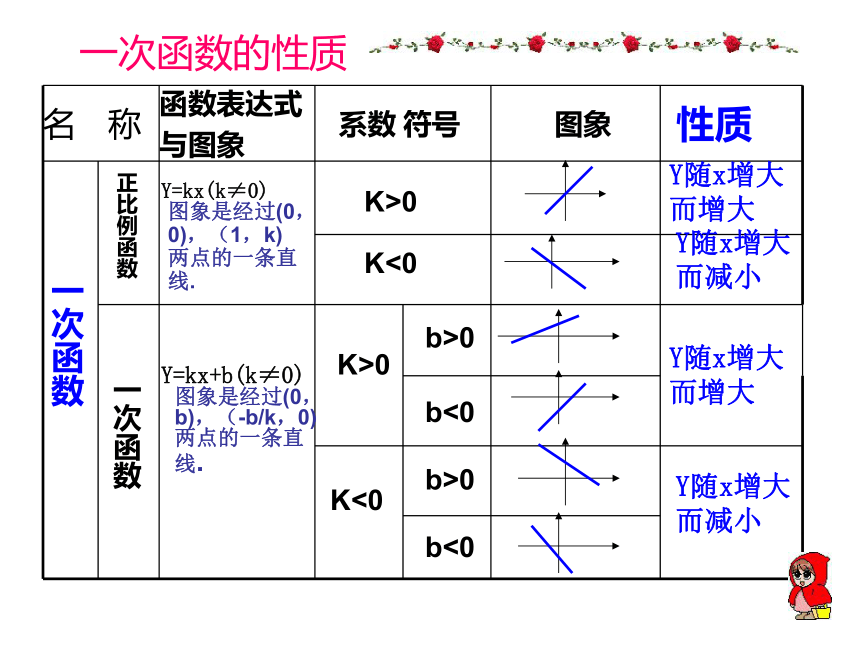
自变量的某一取值,纵坐标y表示与它对应的函数值.把一个函数的自变量x与对应的函数值y分别作为点的横坐标和纵坐标即(x,y),在直角坐标系内描出它的对应点,所有这些点组成的图形叫做函数的图象。一、一次函数的概念:b叫做直线y=kx+b在y轴上的截距,简称截距. k叫做斜率.一次函数y=kx+b(k≠0, k、b为常数)的图象的是一条直线.所以,一次函数y=kx+b的图象也常称为直线y=kx+b.y=kx+b一次函数的性质一次函数正比例函数一次函数Y=kx(k≠0)K>0K<0K>0K<0Y=kx+b(k≠0)b>0b<0b<0b>0Y随x增大而增大Y随x增大而减小Y随x增大而增大Y随x增大而减小图象是经过(0,b),(-b/k,0)两点的一条直线.
图象是经过(0,0),(1,k)两点的一条直线.
例2、求直线y=-2x-3与x轴和y轴的交点,
并画出这条直线.分析:x轴上的点的纵坐标为0,
y轴上的点的横坐标为0.解:直线y=-2x-3与x和y轴的交点分别为(-1.5,0)和(0,-3).作一次函数的图象有什么简便方法?结论:因为一次函数的图象是一条直线,根据两点确定一条直线,只要画出图象上的两个点,就可以画出一次函数的图象.例3、已知一次函数y=kx+b的图象过点(1,3)和(-2,-3), (1)求这个函数的表达式.(2)在同一坐标系下作出y=2x和y=2x+1的图象.待定系数法③一次函数y=2x+1的图像可看成是由直线y=2x向上平移一个单位长度得到。y=2x+1①正比例函数y=kx (k为常数,k≠0)
的图象是一条经过原点的直线。结论:②斜率相等,在y轴截距不相等的两条直线平行.在一次函数y = kx+b中增大上升减小下降kb一次函数y=kx+b的图像和性质经过的象限增减性图像k>0k<0b>0b=0b<0b>0b=0b<0一、二、三一、三一、三、四一、二、四二、四二、三、四y随x的增大
而增大y随x的增大
而增大y随x的增大
而增大y随x的增大
而减小y随x的增大
而减小y随x的增大
而减小3 已知函数(1)当x=0时, y =(2 )当x=2时, y=
(3)当y=0时, x=
(4)当y>0时, x的取值范围 是(6)当-3≤y≤0时, x的取值范围 是(5)当y<1 时, x的取值范围是-311.5X>1.5x<20 ≤ x ≤ 1.51.5能否用待定系数法?这里只知道x、y的一对对应值,条件够吗?已知y是x的反比例函数,当x=2时,y=6.(1)写出y与x的函数关系式
(2)求当x=4时,y的值解:(1)设y与x的函数关系式为∵当x=2时,y=6∴∴∴函数关系式是(2)当x=4时,例 1 (1)y与z成反比例,z与x成正比例;
(2)y与z成反比例,z与3x成反比例;
(3)y与2z成反比例,z与x/2成正比例;例 2将下列各题中y与x的函数关系写出来,
并判断是否是反比例函数.2、已知y1与x成正比例,y2与x成反比例,且
y=y1+y2 , 当x=1时,y=3; 当x=2时y=3;
求y与x之间的函数关系。1、 已知y与x2成反比例,并且当x=3时,y =2.
求x=1.5时y的值.若 y与x2成正比例呢?练一练2.已知y与x-2成反比例,当x=4时,
y=3,求当x=5时,y的值.3.已知y=y1+y2, y1与 成正比例, y2与x2成反比例.当x=1时,y=-12;当x=4时,y=7.求y与x的函数关系式和x的取范围; 1.已知y 与 x 成反比例, 并且当 x = 3 时
y = 7,求 x 与 y 的函数关系式。 作业反比例函数的图象是两支双曲线,它既是轴对称图形又是中心对称图形。有两条对称轴:直线y=x和 y=-x。对称中心是:原点 10.函数 的图象上有三点
(-3,y1), (-1,y2), (2,y3),则函数值y1、y2、y3的
大小关系是_______________;8.已知反比例函数
的图象在 第二、四象限,那么一次函数
y=kx-k的图象经过( )A 第一、二、三象限 B 第一、二、四象限
C 第一、三、四象限 D 第二、三、四象限C9.已知点(-m,n)在反比例函数的图象上,
则它的图象也一定经过点__________(m, -n)y3< y1< y21.如图,点P是反比例函数 在第一象限的图象上的一点,PD⊥x轴于D.则△POD的面积为 .(m,n)1能力提高A.S1>S2
B.S1C.S1 = S2
D.S1和S2的大小关系不能确定. C面积性质(一)5.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的
关系式是 .P(m,n)AoyxB面积性质(二)3.如右图:点B为反比例函数上一点,若图中阴影部分即三角形AOB的面积为4,求反比例函数的解析式.请同学们自己写出结果。例2:已知关于x的一次函数 和 反比例函数 的图象都经过点 (1,-2),求这两个函数的解析式。 m=4,n=-2
写出行驶路程s(千米)与行驶时间t(时)
的关系式。 S=40t1、变量和常量的概念一般地,在一个变化过程中有两个变量,例如x和y,如果对于x的每一个值,y都有唯一的值与之对应,我们就说是x是自变量, y是因变量,也把y叫做x的函数.当x取某一具体值时,y的值就叫做对应于x的函数值。自变量:是指在它的取值范围内可以随心所欲的、
自由自在的取它能取的值,看这概念够贴切了吧?
因变量:这个“因”字是指因x的变化,通过一定的
关系而得到的。2、函数的概念3、函数关系的三种表示方法:解析法、列表法、图象法 课内练习:1.求下列函数中自变量x的取值范围 (1)y = ; (2)y = x2-3x-2;
(3)y = ;(4)y = 2.某小汽车的油箱可装油30 L,每升汽油2.8元,该小汽车原有汽油10 L,现再加汽油x L,求油箱内汽油的总价值y(元)与x(L)之间的函数关系式,并写出自变量的取值范围.x轴或横轴y轴或纵轴坐标原点①两条数轴 ②互相垂直 ③公共原点 ④一般情况下横轴和纵轴具有相同的单位长度 第一象限第二象限第三象限第四象限注 意:坐标轴上的点不属于任何象限。1、平面直角坐标系·AA的横坐标为4A的纵坐标为2有序数对(4, 2)就叫做A的坐标
记作:A(4,2)B(-4,1)MN2、如何确定平面直角坐标系中点的坐标?A(-3,-4)3、已知点的坐标如何来确定点在坐标系内的位置?在坐标系中作出点A(-3,-4)1、能够正确画出直角坐标系。
2、能在直角坐标系中,根据坐标作出点,
由点求出坐标。
3、掌握各象限上及x轴,y轴上点的坐标的
特点:
第一象限(+,+) 第二象限(-,+)
第三象限(-,-)第四象限(+,-)
x轴上的点纵坐标为0,表示为(x,0)
y轴上的点横坐标为0,表示为(0,y)平面直角坐标系4、平行于横轴的直线上的点的纵坐标相同;
平行于纵轴的直线上的点的横坐标相同;P3(-a,-b)P(a,b)5、点P(a,b)关于x轴、y轴、原点对称点的坐标:P1(a,-b)P2(-a,b)6、点P(a,b)到x轴的距离为 ,到y轴的距离为 .(1).求点(2,-3)关于x轴、 y轴、原点对称点的坐标.
(2).若A(a-2,3 )和B(-1,2b+2)关于原点对称,
求a,b得值. 引例:如图是某地一天内的气温变化图.(6,-1)(10,2)(14,5)图像上每一个点的坐标(t,T)表示时间为t时的气温是T.一般来说,函数的图象是由直角坐标系中的一系列
点组成.在图象上每一点的坐标(x,y)中,横坐标x表示
自变量的某一取值,纵坐标y表示与它对应的函数值.把一个函数的自变量x与对应的函数值y分别作为点的横坐标和纵坐标即(x,y),在直角坐标系内描出它的对应点,所有这些点组成的图形叫做函数的图象。一、一次函数的概念:b叫做直线y=kx+b在y轴上的截距,简称截距. k叫做斜率.一次函数y=kx+b(k≠0, k、b为常数)的图象的是一条直线.所以,一次函数y=kx+b的图象也常称为直线y=kx+b.y=kx+b一次函数的性质一次函数正比例函数一次函数Y=kx(k≠0)K>0K<0K>0K<0Y=kx+b(k≠0)b>0b<0b<0b>0Y随x增大而增大Y随x增大而减小Y随x增大而增大Y随x增大而减小图象是经过(0,b),(-b/k,0)两点的一条直线.
图象是经过(0,0),(1,k)两点的一条直线.
例2、求直线y=-2x-3与x轴和y轴的交点,
并画出这条直线.分析:x轴上的点的纵坐标为0,
y轴上的点的横坐标为0.解:直线y=-2x-3与x和y轴的交点分别为(-1.5,0)和(0,-3).作一次函数的图象有什么简便方法?结论:因为一次函数的图象是一条直线,根据两点确定一条直线,只要画出图象上的两个点,就可以画出一次函数的图象.例3、已知一次函数y=kx+b的图象过点(1,3)和(-2,-3), (1)求这个函数的表达式.(2)在同一坐标系下作出y=2x和y=2x+1的图象.待定系数法③一次函数y=2x+1的图像可看成是由直线y=2x向上平移一个单位长度得到。y=2x+1①正比例函数y=kx (k为常数,k≠0)
的图象是一条经过原点的直线。结论:②斜率相等,在y轴截距不相等的两条直线平行.在一次函数y = kx+b中增大上升减小下降kb一次函数y=kx+b的图像和性质经过的象限增减性图像k>0k<0b>0b=0b<0b>0b=0b<0一、二、三一、三一、三、四一、二、四二、四二、三、四y随x的增大
而增大y随x的增大
而增大y随x的增大
而增大y随x的增大
而减小y随x的增大
而减小y随x的增大
而减小3 已知函数(1)当x=0时, y =(2 )当x=2时, y=
(3)当y=0时, x=
(4)当y>0时, x的取值范围 是(6)当-3≤y≤0时, x的取值范围 是(5)当y<1 时, x的取值范围是-311.5X>1.5x<20 ≤ x ≤ 1.51.5能否用待定系数法?这里只知道x、y的一对对应值,条件够吗?已知y是x的反比例函数,当x=2时,y=6.(1)写出y与x的函数关系式
(2)求当x=4时,y的值解:(1)设y与x的函数关系式为∵当x=2时,y=6∴∴∴函数关系式是(2)当x=4时,例 1 (1)y与z成反比例,z与x成正比例;
(2)y与z成反比例,z与3x成反比例;
(3)y与2z成反比例,z与x/2成正比例;例 2将下列各题中y与x的函数关系写出来,
并判断是否是反比例函数.2、已知y1与x成正比例,y2与x成反比例,且
y=y1+y2 , 当x=1时,y=3; 当x=2时y=3;
求y与x之间的函数关系。1、 已知y与x2成反比例,并且当x=3时,y =2.
求x=1.5时y的值.若 y与x2成正比例呢?练一练2.已知y与x-2成反比例,当x=4时,
y=3,求当x=5时,y的值.3.已知y=y1+y2, y1与 成正比例, y2与x2成反比例.当x=1时,y=-12;当x=4时,y=7.求y与x的函数关系式和x的取范围; 1.已知y 与 x 成反比例, 并且当 x = 3 时
y = 7,求 x 与 y 的函数关系式。 作业反比例函数的图象是两支双曲线,它既是轴对称图形又是中心对称图形。有两条对称轴:直线y=x和 y=-x。对称中心是:原点 10.函数 的图象上有三点
(-3,y1), (-1,y2), (2,y3),则函数值y1、y2、y3的
大小关系是_______________;8.已知反比例函数
的图象在 第二、四象限,那么一次函数
y=kx-k的图象经过( )A 第一、二、三象限 B 第一、二、四象限
C 第一、三、四象限 D 第二、三、四象限C9.已知点(-m,n)在反比例函数的图象上,
则它的图象也一定经过点__________(m, -n)y3< y1< y21.如图,点P是反比例函数 在第一象限的图象上的一点,PD⊥x轴于D.则△POD的面积为 .(m,n)1能力提高A.S1>S2
B.S1
D.S1和S2的大小关系不能确定. C面积性质(一)5.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的
关系式是 .P(m,n)AoyxB面积性质(二)3.如右图:点B为反比例函数上一点,若图中阴影部分即三角形AOB的面积为4,求反比例函数的解析式.请同学们自己写出结果。例2:已知关于x的一次函数 和 反比例函数 的图象都经过点 (1,-2),求这两个函数的解析式。 m=4,n=-2
