苏教版选择性必修第一册5.1.1平均变化率同步教学课件(共40张PPT)
文档属性
| 名称 | 苏教版选择性必修第一册5.1.1平均变化率同步教学课件(共40张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-20 22:37:07 | ||
图片预览











文档简介
(共40张PPT)
第5章 导数及其应用
5.1 导数的概念
5.1.1 平均变化率
课标要求
1.通过实例,了解平均变化率的概念,并会求具体函数的平均变化率.2.了解平均变化率概念的形成过程,会在具体的情境中,说明平均变化率的实际意义.
素养要求
1.通过具体的平均变化率问题,培养学生的数学建模素养.2.借助平均变化率的求解,提升学生的数学运算素养.
问题导学预习教材
必备知识探究
内容
索引
互动合作研析题型
关键能力提升
拓展延伸分层精练
核心素养达成
WEN TI DAO XUE YU XI JIAO CAI BI BEI ZHI SHI TAN JIU
问题导学预习教材 必备知识探究
1
1.思考 如图,从数学的角度刻画气温“陡升”,用怎样的数学模型刻画变量变化的快慢程度?
2.填空 (1)函数的平均变化率
(2)平均变化率的意义
平均变化率的几何意义是经过曲线y=f(x)上两点P(x1,y1),Q(x2,y2)的直线PQ的斜率.因此平均变化率是曲线陡峭程度的“________”,或者说,曲线陡峭程度是平均变化率的“________”.
数量化
视觉化
解析 f(2.1)-f(2)=2.12+1-(22+1)=0.41.故选B.
3.做一做 已知函数f(x)=x2+1,则当x由2变到2.1时,函数值的改变量为( )
A.0.40 B.0.41 C.0.43 D.0.44
B
HU DONG HE ZUO YAN XI TI XING GUAN JIAN MENG LI TI SHENG
互动合作研析题型 关键能力提升
2
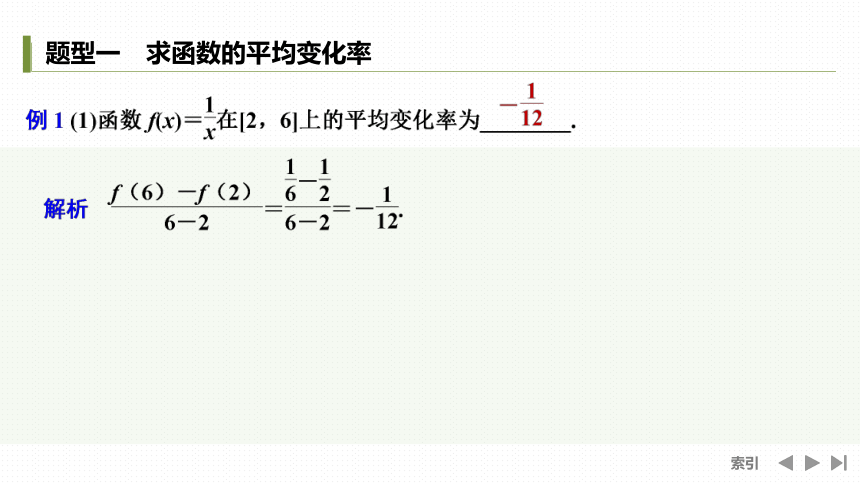
题型一 求函数的平均变化率
思维升华
训练1 某森林公园在过去的10年里,森林占地面积变化如图所示,试分别计算前5年与后5年森林面积的平均变化率.
例2 在高台跳水运动中,运动员相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系h(t)=-4.9t2+6.5t+10.
题型二 实际问题中的平均变化率
(1)求运动员在第一个0.5 s内高度h的平均变化率;
(2)求高度h在1≤t≤2这段时间内的平均变化率.
思维升华
训练2 一质点作直线运动,其位移s与时间t的关系为s(t)=t2+1,该质点在2到2+Δt(Δt>0)之间的平均速度不大于5,则Δt的取值范围是________.
(0,1]
又v≤5,则4+Δt≤5,所以Δt≤1,又Δt>0,所以Δt的取值范围是(0,1].
题型三 平均变化率的应用
例3 为了检测甲、乙两辆车的刹车性能,分别对两辆车进行了测试,甲车从25 m/s到0 m/s花了5 s,乙车从18 m/s到0 m/s花了4 s,试比较两辆车的刹车性能.
平均变化率的应用主要有:求某一时间段内的平均速度,物体受热膨胀率,高度(重量)的平均变化率等等.解决这些问题的关键在于找准自变量和因变量.
思维升华
(2)比较体积V从0 L增加到1 L和从1 L增加到2 L半径r的平均变化率;哪段半径变化较快(精确到0.01)?此结论可说明什么意义?
显然体积V从0 L增加到1 L时,半径变化快,这说明气球刚开始膨胀的比较快,随着体积的增大,半径增加的越来越慢.
课堂小结
2.明确平均变化率的意义
平均变化率的绝对值越大,表示函数值变化得越快,绝对值越小,表示函数值变化得越慢.平均变化率的正负只表示变化的方向.
TUO ZHAN YAN SHEN FEN CENG JING LIAN HE XING SU YANG DA CHENG
拓展延伸分层精练 核心素养达成
3
B
2.已知函数f(x)=x2+2,则该函数在区间[1,3]上的平均变化率为( )
A.4 B.3 C.2 D.1
A
3.一物体的运动方程是s=3+2t,则在[2,2.1]这段时间内的平均变化率为( )
A.0.4 B.2 C.0.3 D.0.2
B
4.某物体的运动方程为s=5-2t2,则该物体在时间[1,1+d]上的平均速度为( )
A.2d+4 B.-2d+4
C.2d-4 D.-2d-4
D
5.函数y=x2在区间[x0,x0+Δx]上的平均变化率为k1,在区间[x0-Δx,x0]上的平均变化率为k2,则( )
A.k1>k2 B.k1C.k1=k2 D.不确定
A
6.函数f(x)=log2x在区间[2,4]上的平均变化率是________.
7.如图所示为物体甲、乙在时间0到t1范围内路程的变化情况,则在0到t0范围内甲的平均速度________乙的平均速度,在t0到t1范围内甲的平均速度________乙的平均速度(填“等于”“大于”或“小于”).
等于
大于
解析 由图可知,在[0,t0]上,甲的平均速度与乙的平均速度相同;在[t0,t1]上,甲的平均速度大于乙的平均速度.
8.若函数y=x3+2在区间[1,a]上的平均变化率为21,则a=________.
4
解得a=4或a=-5.
又∵a>1,∴a=4.
11.如图是函数y=f(x)的图象,函数f(x)在区间[-1,1],[0,2]上的平均变化率分别为m1,m2,则m1,m2的大小关系是( )
B
A.m1>m2 B.m1<m2
C.m1=m2 D.无法确定
12.函数f(x)的图象如图,则函数f(x)在下列区间上平均变化率最大的是( )
C
A.[1,2] B.[2,3]
C.[3,4] D.[4,7]
13.已知函数f(x)=2x2+1.
(1)求函数f(x)在[2,2.01]上的平均变化率;
解 由f(x)=2x2+1,
得f(2.01)-f(2)=0.080 2,
又2.01-2=0.01,
(2)求函数f(x)在[x0,x0+Δx]上的平均变化率.
14.函数f(x)=x,g(x)=x2,h(x)=x3在[0,1]上的平均变化率分别记为m1,m2,m3,则下列结论正确的是( )
A.m1=m2=m3 B.m1>m2>m3
C.m2>m1>m3 D.m1A
本课结束
INNOVATIVE
DESIGN
第5章 导数及其应用
5.1 导数的概念
5.1.1 平均变化率
课标要求
1.通过实例,了解平均变化率的概念,并会求具体函数的平均变化率.2.了解平均变化率概念的形成过程,会在具体的情境中,说明平均变化率的实际意义.
素养要求
1.通过具体的平均变化率问题,培养学生的数学建模素养.2.借助平均变化率的求解,提升学生的数学运算素养.
问题导学预习教材
必备知识探究
内容
索引
互动合作研析题型
关键能力提升
拓展延伸分层精练
核心素养达成
WEN TI DAO XUE YU XI JIAO CAI BI BEI ZHI SHI TAN JIU
问题导学预习教材 必备知识探究
1
1.思考 如图,从数学的角度刻画气温“陡升”,用怎样的数学模型刻画变量变化的快慢程度?
2.填空 (1)函数的平均变化率
(2)平均变化率的意义
平均变化率的几何意义是经过曲线y=f(x)上两点P(x1,y1),Q(x2,y2)的直线PQ的斜率.因此平均变化率是曲线陡峭程度的“________”,或者说,曲线陡峭程度是平均变化率的“________”.
数量化
视觉化
解析 f(2.1)-f(2)=2.12+1-(22+1)=0.41.故选B.
3.做一做 已知函数f(x)=x2+1,则当x由2变到2.1时,函数值的改变量为( )
A.0.40 B.0.41 C.0.43 D.0.44
B
HU DONG HE ZUO YAN XI TI XING GUAN JIAN MENG LI TI SHENG
互动合作研析题型 关键能力提升
2
题型一 求函数的平均变化率
思维升华
训练1 某森林公园在过去的10年里,森林占地面积变化如图所示,试分别计算前5年与后5年森林面积的平均变化率.
例2 在高台跳水运动中,运动员相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系h(t)=-4.9t2+6.5t+10.
题型二 实际问题中的平均变化率
(1)求运动员在第一个0.5 s内高度h的平均变化率;
(2)求高度h在1≤t≤2这段时间内的平均变化率.
思维升华
训练2 一质点作直线运动,其位移s与时间t的关系为s(t)=t2+1,该质点在2到2+Δt(Δt>0)之间的平均速度不大于5,则Δt的取值范围是________.
(0,1]
又v≤5,则4+Δt≤5,所以Δt≤1,又Δt>0,所以Δt的取值范围是(0,1].
题型三 平均变化率的应用
例3 为了检测甲、乙两辆车的刹车性能,分别对两辆车进行了测试,甲车从25 m/s到0 m/s花了5 s,乙车从18 m/s到0 m/s花了4 s,试比较两辆车的刹车性能.
平均变化率的应用主要有:求某一时间段内的平均速度,物体受热膨胀率,高度(重量)的平均变化率等等.解决这些问题的关键在于找准自变量和因变量.
思维升华
(2)比较体积V从0 L增加到1 L和从1 L增加到2 L半径r的平均变化率;哪段半径变化较快(精确到0.01)?此结论可说明什么意义?
显然体积V从0 L增加到1 L时,半径变化快,这说明气球刚开始膨胀的比较快,随着体积的增大,半径增加的越来越慢.
课堂小结
2.明确平均变化率的意义
平均变化率的绝对值越大,表示函数值变化得越快,绝对值越小,表示函数值变化得越慢.平均变化率的正负只表示变化的方向.
TUO ZHAN YAN SHEN FEN CENG JING LIAN HE XING SU YANG DA CHENG
拓展延伸分层精练 核心素养达成
3
B
2.已知函数f(x)=x2+2,则该函数在区间[1,3]上的平均变化率为( )
A.4 B.3 C.2 D.1
A
3.一物体的运动方程是s=3+2t,则在[2,2.1]这段时间内的平均变化率为( )
A.0.4 B.2 C.0.3 D.0.2
B
4.某物体的运动方程为s=5-2t2,则该物体在时间[1,1+d]上的平均速度为( )
A.2d+4 B.-2d+4
C.2d-4 D.-2d-4
D
5.函数y=x2在区间[x0,x0+Δx]上的平均变化率为k1,在区间[x0-Δx,x0]上的平均变化率为k2,则( )
A.k1>k2 B.k1
A
6.函数f(x)=log2x在区间[2,4]上的平均变化率是________.
7.如图所示为物体甲、乙在时间0到t1范围内路程的变化情况,则在0到t0范围内甲的平均速度________乙的平均速度,在t0到t1范围内甲的平均速度________乙的平均速度(填“等于”“大于”或“小于”).
等于
大于
解析 由图可知,在[0,t0]上,甲的平均速度与乙的平均速度相同;在[t0,t1]上,甲的平均速度大于乙的平均速度.
8.若函数y=x3+2在区间[1,a]上的平均变化率为21,则a=________.
4
解得a=4或a=-5.
又∵a>1,∴a=4.
11.如图是函数y=f(x)的图象,函数f(x)在区间[-1,1],[0,2]上的平均变化率分别为m1,m2,则m1,m2的大小关系是( )
B
A.m1>m2 B.m1<m2
C.m1=m2 D.无法确定
12.函数f(x)的图象如图,则函数f(x)在下列区间上平均变化率最大的是( )
C
A.[1,2] B.[2,3]
C.[3,4] D.[4,7]
13.已知函数f(x)=2x2+1.
(1)求函数f(x)在[2,2.01]上的平均变化率;
解 由f(x)=2x2+1,
得f(2.01)-f(2)=0.080 2,
又2.01-2=0.01,
(2)求函数f(x)在[x0,x0+Δx]上的平均变化率.
14.函数f(x)=x,g(x)=x2,h(x)=x3在[0,1]上的平均变化率分别记为m1,m2,m3,则下列结论正确的是( )
A.m1=m2=m3 B.m1>m2>m3
C.m2>m1>m3 D.m1
本课结束
INNOVATIVE
DESIGN
