21.3 实际问题与一元二次方程(2)——平均增长率问题 课件(共27张PPT)
文档属性
| 名称 | 21.3 实际问题与一元二次方程(2)——平均增长率问题 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-20 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
21.3实际问题与一元二次方程(2)
——平均增长率问题
人教版九年级上册
知识回顾
小明上周花了100元,本周比上周多花10%,本周花了______元?
预计下周比本周多花10%,那么下周预计会花_________元?
110
= 110+11 = 121元
100+100×10%
本周花了
下周会花
110
+110×10%
121
理财分析
= 100+10 =110元
已知上周-----求本周-----求下周
谁是理财高手
教学目标
1.掌握建立数学模型以解决增长率与降低率问题.
2.正确分析问题中的数量关系并建立一元二次方程模型.
新知导入
小明上周花了100元,本周比上周多花10%,本周花了______元?
预计下周比本周多花10%,那么下周预计会花_________元?
110
= 110+11 = 121元
100+100×10%
本周花了
下周会花
+110×10%
= 100+10 =110元
若每一周都比上周多花10%
有更好的方法吗 ?
一般思路:已知上周-----求本周-----求下周
有!!!
谁是理财高手(变式)
新知探究
小明上周花了100元,本周比上周多花10%,本周花了______元?
预计下周比本周多花10%,那么下周预计会花_________元?
=100 ×(1+10%)
110
= 100 ×(1+10%)2 =121元
100+100×10%
本周花了
下周会花
=100(1+10%)(1+10%)
× (1+增长率)
×(1+增长率)2
110
上周所花
×(1+10%)
上周所花
一般思路:已知上周 ---求本周----- 求下周
---------------
特殊思路
若每一周都比上周多花10%
(直接二次增长)
=110元
谁是理财高手(变式)
新知探究
上周已花 增长率 本周花了 下周会花
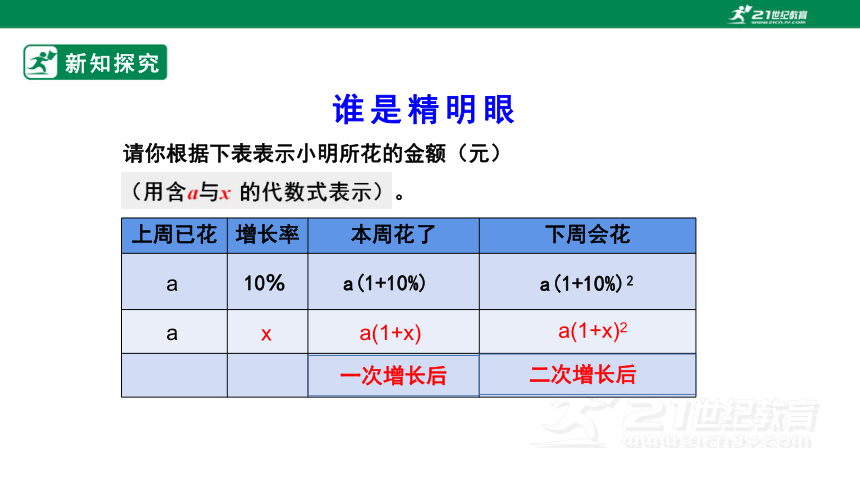
请你根据下表表示小明所花的金额(元)
。
10%
二次增长后
一次增长后
谁是精明眼
a
a
x
a(1+10%)
a(1+10%)2
a(1+x)
a(1+x)2
新知小结
平均增长率问题中的基本数量关系:
如果起始量为a,平均增长率为x,每次的增长率都相同,
那么
二次增长后的量为__________
一次增长后的量为________,
平均增长
模型
a(1+x)
a(1+x)2
主要由a与x决定
例1 金羊网记者从某互联网公司获悉,截止2019年6月,广州投放该公司的单车近2万辆, 给广州市民出行带来巨大的改变。因此,该公司在2020和2021年将继续投放该单车,设这两年投放增长率都为 x 则:
新知探究
(1)截止2020年6月,该单车投放_________万辆;
(2)截止2021年6月,该单车投放__________万辆;
(一次增长)
(二次增长)
找关键词
分析数量关系
新知探究
例1 金羊网记者从某互联网公司获悉,截止2019年6月,广州投放该公司的单车近2万辆, 给广州市民出行带来巨大的改变。因此,该公司在2020和2021年将继续投放该单车,设这两年投放增长率都为 x 则:
(1)截止2020年6月,该单车投放_________万辆;
(2)截止2021年6月,该单车投放__________万辆;
(3)若截止2021年6月,该公司投放单车达到2.88万辆
问这两年的投放增长率是多少?
等量关系2(1+ )2= 2.88
2(1+x)
2(1+x)2
解:设这两年投放单车的平均增长率为 x ,
依题意得:
新知探究
(不符合题意,舍去)
(3)若截止2021年6月,该公司投放单车达到2.88万辆,问这两 年的投放增长率是多少?
答:这两年的投放增长率是20%。
--列(一元二次方程)
--解(直接开平方法)
--验(结果是否合理)
--设(平均增长率)
--答(写结论)
完整解题步骤
2(1+ x )2
= 2.88
( 1+ x )2 = 1.44
1+ x = ±1.2
解得:x1=0.2 x2=-2.2
新知探究
(不符合题意,舍去)
( 1+ x )2 = 1.44
1+ x = ±1.2
2(1+ x )2
(3)若截止2021年6月,该公司投放单车达到2.88万辆,问这两年的投放增长率是多少?
= 2.88
答:这两年的投放增长率是20%。
解:设这两年投放单车的平均增长率为 ,
依题意得:
完整解题步骤
解得:x1=0.2 x2=-2.2
新知探究
(4)在(3)的条件下,如果2021年至2023的增长率相同,那么预计截止2023年6月,该互联网公司的单车要投放大约多少辆?
分析:可知 2021年6月投放2.88万辆,增长率20%
答:该互联网公司的单车要投放大约4.1472万辆。
解 2.88 (1+20%)2 = 4.1472
(二次增长)
新知小结
(5) 验(结果是否合理)
(1) 审 (问题中的等量关系)
(4) 解(直接开平方法)
求二次平均增长率的思路
(2) 设(未知数增长率)
(6) 答 (写结论)
关键是找准
(3) 列(一元二次方程a(1+x)2=b)
选择“共享单车”出行逐渐成为一种潮流和时尚。广州2017年底选择小汽车出行的人约a万,预计每年选择小汽车出行的人数平均下降的百分率为x,请用含: x与a的代数式表示下列结果:
=a(1-x)2
新知探究
(1)到2018年底,选择小汽车出行的人数将降到_________人。
(2)到2019年底,选择小汽车出行的人数将降到___________人。
一次下降
二次下降
找关键词分析数量关系
起始量
平均下降
模型
a-ax
a-2ax+ax2
=a(1-x)
a(1-x)
×(1-x)
起始量
× (1-下降率) 2
a-ax
×(1-下降率)
新知小结
平均下降
模型
平均下降率问题中的基本数量关系:
二次下降后的量为__________
一次下降后的量为__________
与“平均增长模型”有何不同?
口诀:
增长是加下降是减
平均
增长
模型
一次增长后的量为__________
二次增长后的量为__________
a(1+x)
a(1+x)2
a(1-x)
a(1-x)2
新知探究
例2 选择“共享单车” 出行逐渐成为一种潮流和时尚。广州2017年底选择小汽车出行的人约有500万 ,预计到2019年底下降为405万 ,如果这两年选择小汽车出行的人下降的百分率相同,求每年下降的百分率。
二次下降
分析等量关系
2019年底
500
2017年底
405
=405
a(1-x)2
可得500(1-x)2
新知探究
答:每年下降的百分率为10 % 。
--列(一元二次方程)
--解(直接开平方法)
--验(结果是否合理)
--设(平均下降率)
--答
(不符合题意,舍去)
完整解题步骤
例2 选择“共享单车” 出行逐渐成为一种潮流和时尚。广州2017年底选择小汽车出行的人约有500万 ,预计到2019年底下降为405万 ,如果这两年选择小汽车出行的人下降的百分率相同,求每年下降的百分率。
例2(变式)广州2017年底选择小汽车出行的人有500万,预计到2019年底选择小汽车出行人数累计达1355万.如果这两年选择小汽车出行的人下降的百分率相同,求每年下降的百分率。
新知探究
分析
解:设每年下降的百分率为 x ,依题意得:
时间
人数(万)
下降率
500
2017
2019
1355
2018
累计
500(1-x)
500(1-x)2
x
x
列出方程 500+500(1-x)+500(1-x)2 =1355
新知探究
例2(变式)广州2017年底选择小汽车出行的人有500万,预计到2019年底选择小汽车出行人数累计达1355万.如果这两年选择小汽车出行的人下降的百分率相同,求每年下降的百分率。
解:设每年下降的百分率为 x ,依题意得:
500+500(1-x)+500(1-x)2 =1355
答:每年下降的百分率为10 % 。
(不符合题意,舍去)
1+(1-x)+(1-x)2 =2.71
x2-3x+0.29 =0
解得:x1=0.1 x2=2.9
--列(一元二次方程)
--解(直接开平方法)
--验(结果是否合理)
--设(平均下降率)
--答
解(方 程)
新知小结
【 3种主要模型】
(1)若起始量为a,终止量为b,平均增长率为x,则二次平均增长问题:a(1+x)2=b
典型例题一
2(1+x)2=2.88
(2)若起始量为a,终止量为b,平均下降率为x,则二次平均下降问题:a(1-x)2=b
典型例题二
500(1-x)2=405
(3)若起始量为a,3个连续量的“和”为c,平均变化率(增长或下降)为x,
则可得:a+a(1+x)+a(1+x)2=c
或者 a+a(1-x)+a(1-x)2=c
典型例题二变式
500+500(1-x)+500(1-x)2=1355
新知练习
1.两年前生产1吨甲种药品的成本是5000元。随着生产技术的进步,现在生产1吨甲种药品的成本是4050元,若设甲种药品成本的年平均下降率为 x ,依题意可列方程为( )
C
A. 4050(1-x)2=5000 B.5000(1+x)2=4050
C. 5000(1-x)2=4050 D.4050(1+x)2=5000
分析:利用二次下降模型a(1-x)2=b
新知练习
2.两年前生产1吨甲种药品的成本是5000元。随着生产技术的进步,
现在生产1吨甲种药品的成本是4050元,
(1)求甲种药品成本的年平均下降率是多少?
解:设甲种药品成本的年平均下降率为 x ,依题意可列方程为
即年平均下降率为 10 %
5000(1-x)2=4050
解得 x1=1.9(舍去) x2=0.1
新知练习
2.两年前生产1吨甲种药品的成本是5000元。随着生产技术的进步,
现在生产1吨甲种药品的成本是4050元,
(1)求甲种药品成本的年平均下降率是多少?(10 %)
(2)为了获取更大利润,厂家拟每年都对成本保持前两次的下降处理,请你预计两年后的成本是多少?
答:两年后的成本是3280.5 元。
解: 4050 (1-10%)2 =3280.5(元)
新知练习
3.某超市一月份的营业额为36万元,三月份的营业额为48万元,
设每月的平均增长率为x ,根据题意可列方程为______________
36(1+x)2=48
分析:利用二次增长模型:a(1+x)2=b
分析 :关键词“第一季度”,是典型求和问题
变式:
某超市一月份的营业额为36万元,若每月增长率相同,
第一季度营业额为120万元。设每月的平均增长率为 x ,根据题
意可列方程为___________________________
36
+36(1+x)
+36(1+x)2
=120
课堂总结
平均变化率问题
增长率问题
a(1+x)2=b,其中 a 为增长前的量,x 为增长率,2 为增长次数,b 为增长后的量.
降低率问题
a(1-x)2=b,其中 a 为降低前的量,x 为降低率,2 为降低次数,b 为降低后的量.注意 1 与 x 位置不可调换.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
21.3实际问题与一元二次方程(2)
——平均增长率问题
人教版九年级上册
知识回顾
小明上周花了100元,本周比上周多花10%,本周花了______元?
预计下周比本周多花10%,那么下周预计会花_________元?
110
= 110+11 = 121元
100+100×10%
本周花了
下周会花
110
+110×10%
121
理财分析
= 100+10 =110元
已知上周-----求本周-----求下周
谁是理财高手
教学目标
1.掌握建立数学模型以解决增长率与降低率问题.
2.正确分析问题中的数量关系并建立一元二次方程模型.
新知导入
小明上周花了100元,本周比上周多花10%,本周花了______元?
预计下周比本周多花10%,那么下周预计会花_________元?
110
= 110+11 = 121元
100+100×10%
本周花了
下周会花
+110×10%
= 100+10 =110元
若每一周都比上周多花10%
有更好的方法吗 ?
一般思路:已知上周-----求本周-----求下周
有!!!
谁是理财高手(变式)
新知探究
小明上周花了100元,本周比上周多花10%,本周花了______元?
预计下周比本周多花10%,那么下周预计会花_________元?
=100 ×(1+10%)
110
= 100 ×(1+10%)2 =121元
100+100×10%
本周花了
下周会花
=100(1+10%)(1+10%)
× (1+增长率)
×(1+增长率)2
110
上周所花
×(1+10%)
上周所花
一般思路:已知上周 ---求本周----- 求下周
---------------
特殊思路
若每一周都比上周多花10%
(直接二次增长)
=110元
谁是理财高手(变式)
新知探究
上周已花 增长率 本周花了 下周会花
请你根据下表表示小明所花的金额(元)
。
10%
二次增长后
一次增长后
谁是精明眼
a
a
x
a(1+10%)
a(1+10%)2
a(1+x)
a(1+x)2
新知小结
平均增长率问题中的基本数量关系:
如果起始量为a,平均增长率为x,每次的增长率都相同,
那么
二次增长后的量为__________
一次增长后的量为________,
平均增长
模型
a(1+x)
a(1+x)2
主要由a与x决定
例1 金羊网记者从某互联网公司获悉,截止2019年6月,广州投放该公司的单车近2万辆, 给广州市民出行带来巨大的改变。因此,该公司在2020和2021年将继续投放该单车,设这两年投放增长率都为 x 则:
新知探究
(1)截止2020年6月,该单车投放_________万辆;
(2)截止2021年6月,该单车投放__________万辆;
(一次增长)
(二次增长)
找关键词
分析数量关系
新知探究
例1 金羊网记者从某互联网公司获悉,截止2019年6月,广州投放该公司的单车近2万辆, 给广州市民出行带来巨大的改变。因此,该公司在2020和2021年将继续投放该单车,设这两年投放增长率都为 x 则:
(1)截止2020年6月,该单车投放_________万辆;
(2)截止2021年6月,该单车投放__________万辆;
(3)若截止2021年6月,该公司投放单车达到2.88万辆
问这两年的投放增长率是多少?
等量关系2(1+ )2= 2.88
2(1+x)
2(1+x)2
解:设这两年投放单车的平均增长率为 x ,
依题意得:
新知探究
(不符合题意,舍去)
(3)若截止2021年6月,该公司投放单车达到2.88万辆,问这两 年的投放增长率是多少?
答:这两年的投放增长率是20%。
--列(一元二次方程)
--解(直接开平方法)
--验(结果是否合理)
--设(平均增长率)
--答(写结论)
完整解题步骤
2(1+ x )2
= 2.88
( 1+ x )2 = 1.44
1+ x = ±1.2
解得:x1=0.2 x2=-2.2
新知探究
(不符合题意,舍去)
( 1+ x )2 = 1.44
1+ x = ±1.2
2(1+ x )2
(3)若截止2021年6月,该公司投放单车达到2.88万辆,问这两年的投放增长率是多少?
= 2.88
答:这两年的投放增长率是20%。
解:设这两年投放单车的平均增长率为 ,
依题意得:
完整解题步骤
解得:x1=0.2 x2=-2.2
新知探究
(4)在(3)的条件下,如果2021年至2023的增长率相同,那么预计截止2023年6月,该互联网公司的单车要投放大约多少辆?
分析:可知 2021年6月投放2.88万辆,增长率20%
答:该互联网公司的单车要投放大约4.1472万辆。
解 2.88 (1+20%)2 = 4.1472
(二次增长)
新知小结
(5) 验(结果是否合理)
(1) 审 (问题中的等量关系)
(4) 解(直接开平方法)
求二次平均增长率的思路
(2) 设(未知数增长率)
(6) 答 (写结论)
关键是找准
(3) 列(一元二次方程a(1+x)2=b)
选择“共享单车”出行逐渐成为一种潮流和时尚。广州2017年底选择小汽车出行的人约a万,预计每年选择小汽车出行的人数平均下降的百分率为x,请用含: x与a的代数式表示下列结果:
=a(1-x)2
新知探究
(1)到2018年底,选择小汽车出行的人数将降到_________人。
(2)到2019年底,选择小汽车出行的人数将降到___________人。
一次下降
二次下降
找关键词分析数量关系
起始量
平均下降
模型
a-ax
a-2ax+ax2
=a(1-x)
a(1-x)
×(1-x)
起始量
× (1-下降率) 2
a-ax
×(1-下降率)
新知小结
平均下降
模型
平均下降率问题中的基本数量关系:
二次下降后的量为__________
一次下降后的量为__________
与“平均增长模型”有何不同?
口诀:
增长是加下降是减
平均
增长
模型
一次增长后的量为__________
二次增长后的量为__________
a(1+x)
a(1+x)2
a(1-x)
a(1-x)2
新知探究
例2 选择“共享单车” 出行逐渐成为一种潮流和时尚。广州2017年底选择小汽车出行的人约有500万 ,预计到2019年底下降为405万 ,如果这两年选择小汽车出行的人下降的百分率相同,求每年下降的百分率。
二次下降
分析等量关系
2019年底
500
2017年底
405
=405
a(1-x)2
可得500(1-x)2
新知探究
答:每年下降的百分率为10 % 。
--列(一元二次方程)
--解(直接开平方法)
--验(结果是否合理)
--设(平均下降率)
--答
(不符合题意,舍去)
完整解题步骤
例2 选择“共享单车” 出行逐渐成为一种潮流和时尚。广州2017年底选择小汽车出行的人约有500万 ,预计到2019年底下降为405万 ,如果这两年选择小汽车出行的人下降的百分率相同,求每年下降的百分率。
例2(变式)广州2017年底选择小汽车出行的人有500万,预计到2019年底选择小汽车出行人数累计达1355万.如果这两年选择小汽车出行的人下降的百分率相同,求每年下降的百分率。
新知探究
分析
解:设每年下降的百分率为 x ,依题意得:
时间
人数(万)
下降率
500
2017
2019
1355
2018
累计
500(1-x)
500(1-x)2
x
x
列出方程 500+500(1-x)+500(1-x)2 =1355
新知探究
例2(变式)广州2017年底选择小汽车出行的人有500万,预计到2019年底选择小汽车出行人数累计达1355万.如果这两年选择小汽车出行的人下降的百分率相同,求每年下降的百分率。
解:设每年下降的百分率为 x ,依题意得:
500+500(1-x)+500(1-x)2 =1355
答:每年下降的百分率为10 % 。
(不符合题意,舍去)
1+(1-x)+(1-x)2 =2.71
x2-3x+0.29 =0
解得:x1=0.1 x2=2.9
--列(一元二次方程)
--解(直接开平方法)
--验(结果是否合理)
--设(平均下降率)
--答
解(方 程)
新知小结
【 3种主要模型】
(1)若起始量为a,终止量为b,平均增长率为x,则二次平均增长问题:a(1+x)2=b
典型例题一
2(1+x)2=2.88
(2)若起始量为a,终止量为b,平均下降率为x,则二次平均下降问题:a(1-x)2=b
典型例题二
500(1-x)2=405
(3)若起始量为a,3个连续量的“和”为c,平均变化率(增长或下降)为x,
则可得:a+a(1+x)+a(1+x)2=c
或者 a+a(1-x)+a(1-x)2=c
典型例题二变式
500+500(1-x)+500(1-x)2=1355
新知练习
1.两年前生产1吨甲种药品的成本是5000元。随着生产技术的进步,现在生产1吨甲种药品的成本是4050元,若设甲种药品成本的年平均下降率为 x ,依题意可列方程为( )
C
A. 4050(1-x)2=5000 B.5000(1+x)2=4050
C. 5000(1-x)2=4050 D.4050(1+x)2=5000
分析:利用二次下降模型a(1-x)2=b
新知练习
2.两年前生产1吨甲种药品的成本是5000元。随着生产技术的进步,
现在生产1吨甲种药品的成本是4050元,
(1)求甲种药品成本的年平均下降率是多少?
解:设甲种药品成本的年平均下降率为 x ,依题意可列方程为
即年平均下降率为 10 %
5000(1-x)2=4050
解得 x1=1.9(舍去) x2=0.1
新知练习
2.两年前生产1吨甲种药品的成本是5000元。随着生产技术的进步,
现在生产1吨甲种药品的成本是4050元,
(1)求甲种药品成本的年平均下降率是多少?(10 %)
(2)为了获取更大利润,厂家拟每年都对成本保持前两次的下降处理,请你预计两年后的成本是多少?
答:两年后的成本是3280.5 元。
解: 4050 (1-10%)2 =3280.5(元)
新知练习
3.某超市一月份的营业额为36万元,三月份的营业额为48万元,
设每月的平均增长率为x ,根据题意可列方程为______________
36(1+x)2=48
分析:利用二次增长模型:a(1+x)2=b
分析 :关键词“第一季度”,是典型求和问题
变式:
某超市一月份的营业额为36万元,若每月增长率相同,
第一季度营业额为120万元。设每月的平均增长率为 x ,根据题
意可列方程为___________________________
36
+36(1+x)
+36(1+x)2
=120
课堂总结
平均变化率问题
增长率问题
a(1+x)2=b,其中 a 为增长前的量,x 为增长率,2 为增长次数,b 为增长后的量.
降低率问题
a(1-x)2=b,其中 a 为降低前的量,x 为降低率,2 为降低次数,b 为降低后的量.注意 1 与 x 位置不可调换.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
