1.2 反比例函数在求图形面积中的应用 同步练习(含解析)
文档属性
| 名称 | 1.2 反比例函数在求图形面积中的应用 同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第一章 反比例函数
反比例函数在求图形面积中的应用
应用1 反比例函数的比例系数k与面积的关系
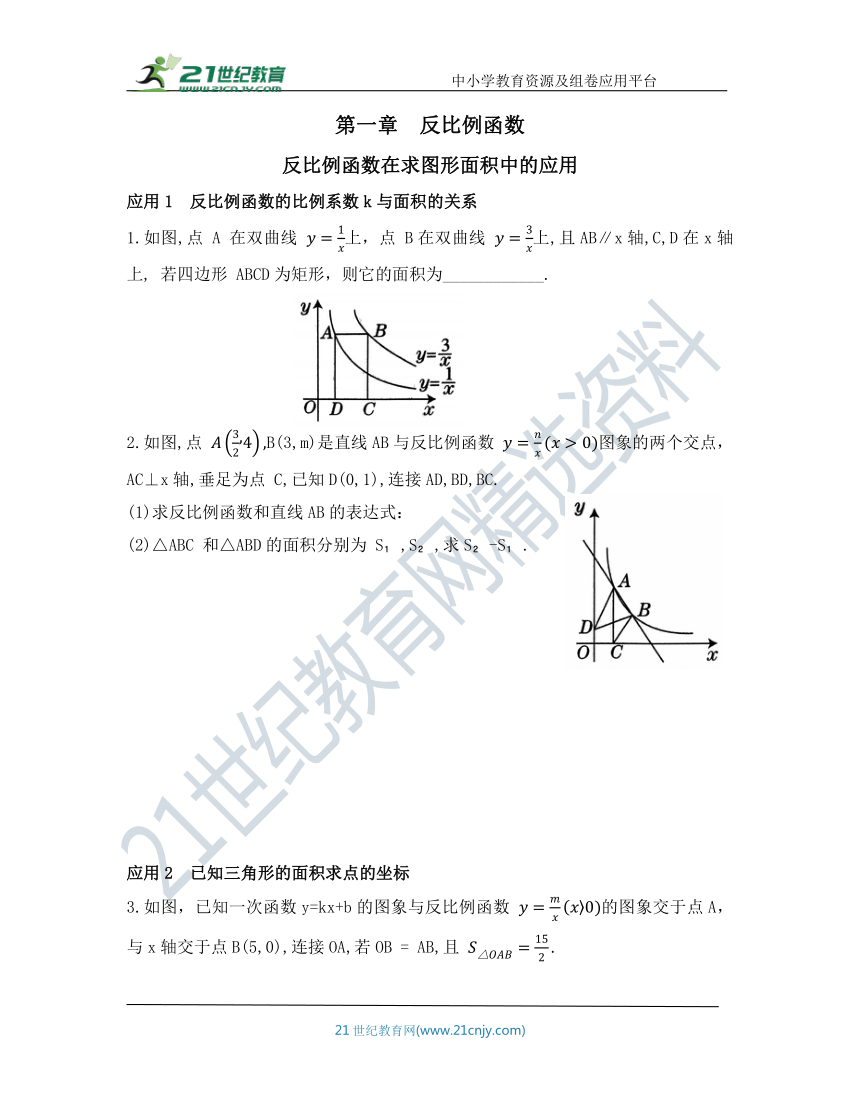
1.如图,点 A 在双曲线 上,点 B在双曲线 上,且AB∥x轴,C,D在x轴上, 若四边形 ABCD为矩形,则它的面积为____________.
2.如图,点 B(3,m)是直线AB与反比例函数 图象的两个交点,AC⊥x轴,垂足为点 C,已知D(0,1),连接AD,BD,BC.
(1)求反比例函数和直线AB的表达式:
(2)△ABC 和△ABD的面积分别为 S ,S ,求S -S .
应用2 已知三角形的面积求点的坐标
3.如图,已知一次函数y=kx+b的图象与反比例函数 的图象交于点A,与x轴交于点B(5,0),连接OA,若OB = AB,且
(1)求反比例函数与一次函数的表达式;
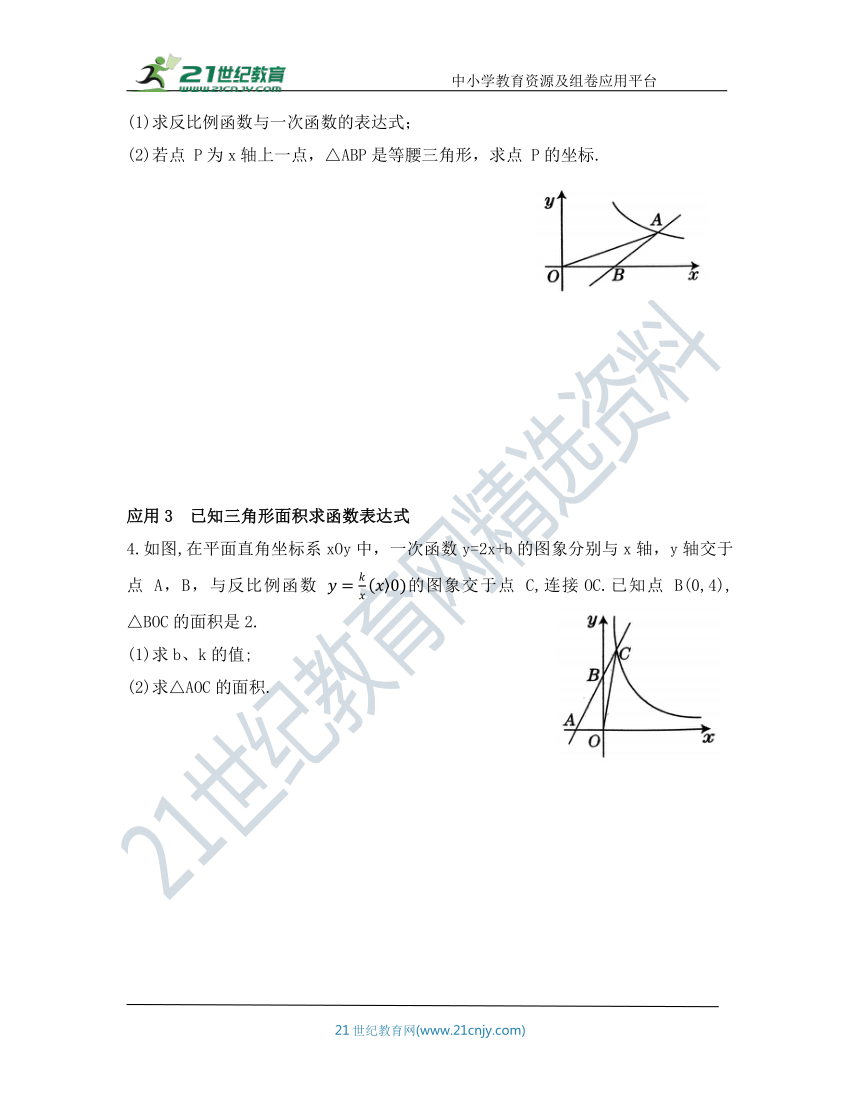
(2)若点 P为x轴上一点,△ABP是等腰三角形,求点 P的坐标.
应用3 已知三角形面积求函数表达式
4.如图,在平面直角坐标系xOy中,一次函数y=2x+b的图象分别与x轴,y轴交于点 A,B,与反比例函数 的图象交于点 C,连接OC.已知点 B(0,4), △BOC的面积是2.
(1)求b、k的值;
(2)求△AOC的面积.
应用4 已知四边形面积求函数表达式
5.如图,矩形ABOD的顶点 A是函数y=-x-(k+1)的图象与函数 在第二象限的图象的交点,B,D 两点在坐标轴上,且矩形ABOD的面积为3.
(1)求两函数的表达式;
(2)求两函数图象的交点A,C 的坐标;
(3)若点P是y轴上一动点,且 求点P的坐标.
应用5 已知反比例函数表达式求图形的面积
题型1 利用函数表达式求面积
6.如图,直线y=2x与反比例函数 x>0)的图象交于点A(1,a),点 B是此反比例函数图象上任意一点(不与点 A 重合),BC⊥x轴于点 C.
(1)求k的值;
(2)求△OBC的面积.
题型2 利用对称性求面积
7.如图,反比例函数 0)与正比例函数 y=mx(m≠0)的图象交于点A(-1,2)和点 B,点 C是点A关于y轴的对称点,连接AC,BC.
(1)求该反比例函数的表达式;
(2)求△ABC的面积;
(3)请结合函数图象,直接写出不等式 的解集.
题型3 利用点的坐标及面积公式求面积
8.如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与反比例函数的图象都经过A(2,-4),B(-4,m)两点.
(1)求反比例函数和一次函数的表达式;
(2)过O、A两点的直线与反比例函数图象交于另一点C,连接BC,求△ABC的面积.
参考答案
1.2 【点拨】过点 A作AE⊥y轴,垂足为E.∵点A在双曲线 上,点B在双曲线 上,四边形ABCD为矩形,∴矩形AEOD的面积为1,矩形BEOC的面积为3.∴矩形ABCD的面积为3-1=2.
2.【解】(1)∵点 在反比例函数 的图象上,
∴反比例函数的表达式为
将点B(3,m)代入 得m=2,∴B(3,2).
设直线AB的表达式为y=hx+b,把点A,B的坐标分别代入,
得 解得 ∴直线AB的表达式为
(2)由点A坐标得AC=4,点 B到AC的距离为3-
设AB与y轴的交点为 E,易得E(0,6).∴DE=6-1=5.
3.【解】(1)如图,过点 A作AD⊥x轴于点 D.
∵B(5,0),∴OB=5.
∴AD=3.∵OB=AB,∴AB=5.
在 Rt△ADB中, ∴OD=OB+BD=9.
∴A(9,3).将点A 的坐标代入 得m=9×3=27,
∴反比例函数的表达式为
将点 A,B的坐标分别代入 y = kx+b,得: 解得
∴一次函数的表达式为
(2)由(1)知AB=5.分三种情况讨论:
①当AB=PB时,PB=5.∴P(0,0)或P(10,0).
②当AB=AP时,如图.由(1)知BD=4,AD⊥x轴,易知点P与点 B关于直线AD对称,
∴DP=BD=4.∴OP=5+4+4=13,∴P(13,0).
③当BP=AP 时,设P(a,0),∵A(9,3),B(5,0),∴AP =(9-a) +9,BP =(5-a) .
∴(9-a) +9=(5-a) ,解得
综上,满足条件的点 P的坐标为(0,0)或(10,0)或(13,0)或
4.【解】(1)∵一次函数y=2x+b的图象交y轴于点B(0,4),∴b=4,OB=4,
∴一次函数的表达式为y=2x+4.设点 C(m,n).
∵△BOC的面积是 解得m=1.
∵点C在一次函数图象上,∴n=2+4=6,∴点 C(1,6).
把点 C(1,6)的坐标代入 得k=6.
(2)对于y=2x+4,当y=0时,0=2x+4,解得x=-2,
∴点
5.【解】(1)由图象知k<0,由已知条件得|k|=3,∴k= -3.
∴反比例函数的表达式为 一次函数的表达式为y=-x+2.
(2)由 解得
∵点A在第二象限,点C在第四象限,∴点A,C的坐标分别为(-1,3),(3,-1).
(3)设点P的坐标为(0,m),直线y=-x+2与y轴的交点为 M,则点 M的坐标为(0,2).
即
或 ∴点P的坐标为 或
6.【解】(1)∵直线y=2x与反比例函数 x>0)的图象交于点A(1,a),
∴将A(1,a)的坐标代入 y=2x,得a=2,∴A(1,2).
将A(1,2)的坐标代入反比例函数 中,得k=2.
(2)∵点B是反比例函数 图象上的点,且BC⊥x轴于点C,
∴△OBC 的面积为
7.【解】(1)把点 A(-1,2)的坐标代入 0),得
∴该反比例函数的表达式为
(2)易知点 B(1,-2).
∵点C是点A关于y轴的对称点,∴C(1,2),∴CA=2,CA⊥CB,
(3)根据图象得不等式 的解集为x<-1或08.【解】(1)将点A(2,-4)的坐标代入 得到则k=-8.
∴反比例函数的表达式为
将点B(-4,m)的坐标代入 得 ∴B(-4,2).
将点A,B的坐标分别代入y=ax+b,得 解得
∴一次函数的表达式为y=-x-2.
(2)如图,设AB交x轴于点 D,连接CD,过点 A 作 AE⊥CD交 CD 延长线于点E,作BF⊥CD交CD于点 F.
令y=-x-2=0,则x= -2,∴点D的坐标为(-2,0).
∵过O、A两点的直线与反比例函数图象交于另一点C,
∴A(2,-4)与点 C关于原点对称,∴点C(-2,4),
∴点C、点D横坐标相同,∴CD∥y轴,
21世纪教育网(www.21cnjy.com)
第一章 反比例函数
反比例函数在求图形面积中的应用
应用1 反比例函数的比例系数k与面积的关系
1.如图,点 A 在双曲线 上,点 B在双曲线 上,且AB∥x轴,C,D在x轴上, 若四边形 ABCD为矩形,则它的面积为____________.
2.如图,点 B(3,m)是直线AB与反比例函数 图象的两个交点,AC⊥x轴,垂足为点 C,已知D(0,1),连接AD,BD,BC.
(1)求反比例函数和直线AB的表达式:
(2)△ABC 和△ABD的面积分别为 S ,S ,求S -S .
应用2 已知三角形的面积求点的坐标
3.如图,已知一次函数y=kx+b的图象与反比例函数 的图象交于点A,与x轴交于点B(5,0),连接OA,若OB = AB,且
(1)求反比例函数与一次函数的表达式;
(2)若点 P为x轴上一点,△ABP是等腰三角形,求点 P的坐标.
应用3 已知三角形面积求函数表达式
4.如图,在平面直角坐标系xOy中,一次函数y=2x+b的图象分别与x轴,y轴交于点 A,B,与反比例函数 的图象交于点 C,连接OC.已知点 B(0,4), △BOC的面积是2.
(1)求b、k的值;
(2)求△AOC的面积.
应用4 已知四边形面积求函数表达式
5.如图,矩形ABOD的顶点 A是函数y=-x-(k+1)的图象与函数 在第二象限的图象的交点,B,D 两点在坐标轴上,且矩形ABOD的面积为3.
(1)求两函数的表达式;
(2)求两函数图象的交点A,C 的坐标;
(3)若点P是y轴上一动点,且 求点P的坐标.
应用5 已知反比例函数表达式求图形的面积
题型1 利用函数表达式求面积
6.如图,直线y=2x与反比例函数 x>0)的图象交于点A(1,a),点 B是此反比例函数图象上任意一点(不与点 A 重合),BC⊥x轴于点 C.
(1)求k的值;
(2)求△OBC的面积.
题型2 利用对称性求面积
7.如图,反比例函数 0)与正比例函数 y=mx(m≠0)的图象交于点A(-1,2)和点 B,点 C是点A关于y轴的对称点,连接AC,BC.
(1)求该反比例函数的表达式;
(2)求△ABC的面积;
(3)请结合函数图象,直接写出不等式 的解集.
题型3 利用点的坐标及面积公式求面积
8.如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与反比例函数的图象都经过A(2,-4),B(-4,m)两点.
(1)求反比例函数和一次函数的表达式;
(2)过O、A两点的直线与反比例函数图象交于另一点C,连接BC,求△ABC的面积.
参考答案
1.2 【点拨】过点 A作AE⊥y轴,垂足为E.∵点A在双曲线 上,点B在双曲线 上,四边形ABCD为矩形,∴矩形AEOD的面积为1,矩形BEOC的面积为3.∴矩形ABCD的面积为3-1=2.
2.【解】(1)∵点 在反比例函数 的图象上,
∴反比例函数的表达式为
将点B(3,m)代入 得m=2,∴B(3,2).
设直线AB的表达式为y=hx+b,把点A,B的坐标分别代入,
得 解得 ∴直线AB的表达式为
(2)由点A坐标得AC=4,点 B到AC的距离为3-
设AB与y轴的交点为 E,易得E(0,6).∴DE=6-1=5.
3.【解】(1)如图,过点 A作AD⊥x轴于点 D.
∵B(5,0),∴OB=5.
∴AD=3.∵OB=AB,∴AB=5.
在 Rt△ADB中, ∴OD=OB+BD=9.
∴A(9,3).将点A 的坐标代入 得m=9×3=27,
∴反比例函数的表达式为
将点 A,B的坐标分别代入 y = kx+b,得: 解得
∴一次函数的表达式为
(2)由(1)知AB=5.分三种情况讨论:
①当AB=PB时,PB=5.∴P(0,0)或P(10,0).
②当AB=AP时,如图.由(1)知BD=4,AD⊥x轴,易知点P与点 B关于直线AD对称,
∴DP=BD=4.∴OP=5+4+4=13,∴P(13,0).
③当BP=AP 时,设P(a,0),∵A(9,3),B(5,0),∴AP =(9-a) +9,BP =(5-a) .
∴(9-a) +9=(5-a) ,解得
综上,满足条件的点 P的坐标为(0,0)或(10,0)或(13,0)或
4.【解】(1)∵一次函数y=2x+b的图象交y轴于点B(0,4),∴b=4,OB=4,
∴一次函数的表达式为y=2x+4.设点 C(m,n).
∵△BOC的面积是 解得m=1.
∵点C在一次函数图象上,∴n=2+4=6,∴点 C(1,6).
把点 C(1,6)的坐标代入 得k=6.
(2)对于y=2x+4,当y=0时,0=2x+4,解得x=-2,
∴点
5.【解】(1)由图象知k<0,由已知条件得|k|=3,∴k= -3.
∴反比例函数的表达式为 一次函数的表达式为y=-x+2.
(2)由 解得
∵点A在第二象限,点C在第四象限,∴点A,C的坐标分别为(-1,3),(3,-1).
(3)设点P的坐标为(0,m),直线y=-x+2与y轴的交点为 M,则点 M的坐标为(0,2).
即
或 ∴点P的坐标为 或
6.【解】(1)∵直线y=2x与反比例函数 x>0)的图象交于点A(1,a),
∴将A(1,a)的坐标代入 y=2x,得a=2,∴A(1,2).
将A(1,2)的坐标代入反比例函数 中,得k=2.
(2)∵点B是反比例函数 图象上的点,且BC⊥x轴于点C,
∴△OBC 的面积为
7.【解】(1)把点 A(-1,2)的坐标代入 0),得
∴该反比例函数的表达式为
(2)易知点 B(1,-2).
∵点C是点A关于y轴的对称点,∴C(1,2),∴CA=2,CA⊥CB,
(3)根据图象得不等式 的解集为x<-1或0
∴反比例函数的表达式为
将点B(-4,m)的坐标代入 得 ∴B(-4,2).
将点A,B的坐标分别代入y=ax+b,得 解得
∴一次函数的表达式为y=-x-2.
(2)如图,设AB交x轴于点 D,连接CD,过点 A 作 AE⊥CD交 CD 延长线于点E,作BF⊥CD交CD于点 F.
令y=-x-2=0,则x= -2,∴点D的坐标为(-2,0).
∵过O、A两点的直线与反比例函数图象交于另一点C,
∴A(2,-4)与点 C关于原点对称,∴点C(-2,4),
∴点C、点D横坐标相同,∴CD∥y轴,
21世纪教育网(www.21cnjy.com)
