宁阳第二实验中学第一次阶段性考试九年级数学试题
文档属性
| 名称 | 宁阳第二实验中学第一次阶段性考试九年级数学试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 69.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-11-02 00:00:00 | ||
图片预览



文档简介
宁阳第二实验中学第一次阶段性考试
初三数学试题卷一
选择题(每题3分,共60分)
下列多边形一定相似的为( )
A. 两个矩形 B. 两个菱形
C. 两个正方形 D. 两个平行四边形
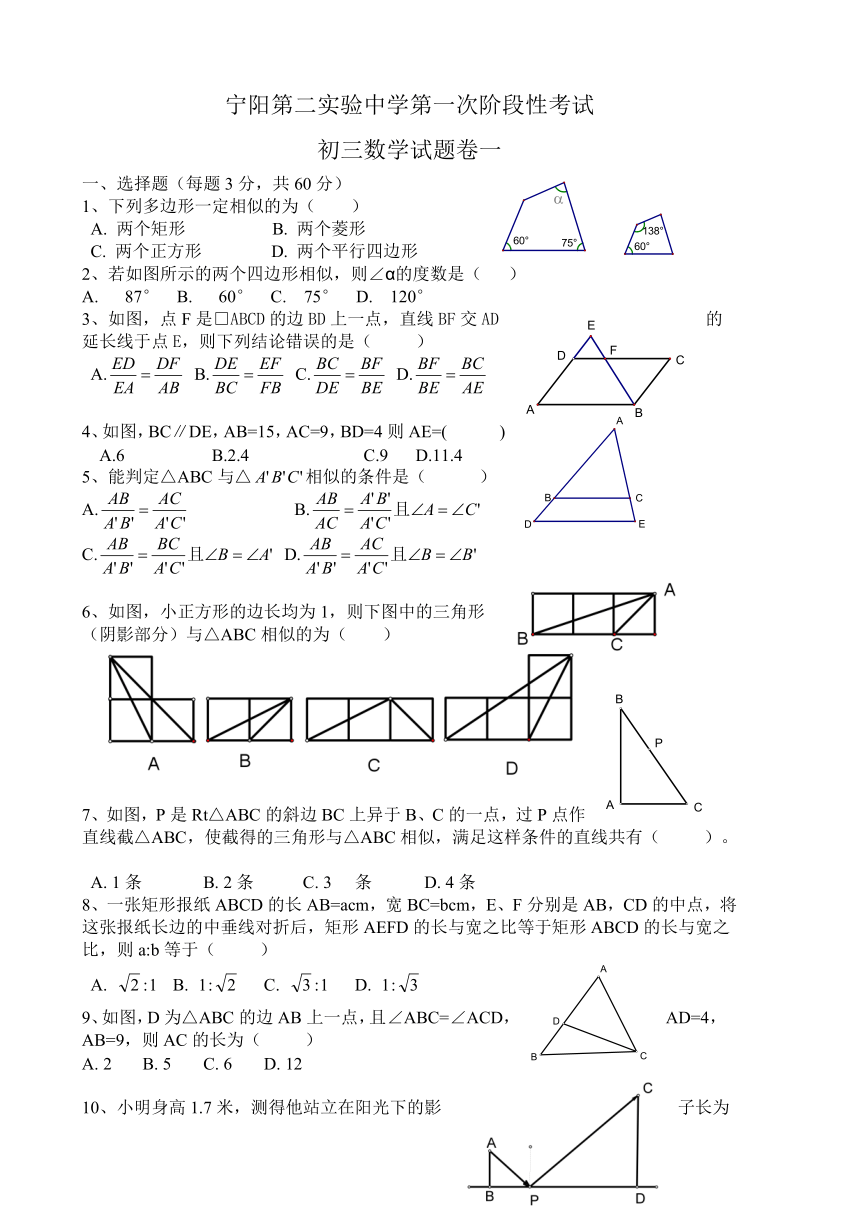
2、若如图所示的两个四边形相似,则∠α的度数是( )
A. 87° B. 60° C. 75° D. 120°
3、如图,点F是□ABCD的边BD上一点,直线BF交AD的延长线于点E,则下列结论错误的是( )
A. B. C. D.
4、如图,BC∥DE,AB=15,AC=9,BD=4则AE=( )
A.6 B.2.4 C.9 D.11.4
5、能判定△ABC与△相似的条件是( )A. B.
C. D.
6、如图,小正方形的边长均为1,则下图中的三角形
(阴影部分)与△ABC相似的为( )
7、如图,P是Rt△ABC的斜边BC上异 ( http: / / www.21cnjy.com )于B、C的一点,过P点作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有( )。
A. 1条 B. 2条 C. 3 条 D. 4条
8、一张矩形报纸ABCD的长AB=acm, ( http: / / www.21cnjy.com )宽BC=bcm,E、F分别是AB,CD的中点,将这张报纸长边的中垂线对折后,矩形AEFD的长与宽之比等于矩形ABCD的长与宽之比,则a:b等于( )
A. B. C. D.
9、如图,D为△ABC的边AB上一点,且∠ABC=∠ACD,AD=4,AB=9,则AC的长为( )
A. 2 B. 5 C. 6 D. 12
10、小明身高1.7米,测得他站立在阳光下 ( http: / / www.21cnjy.com )的影子长为0.85米,紧接着他把手臂竖直举起,测得影子长为1.1米,那么小明举起的手臂超过头顶( )。
A. 0.5米 B. 0.55米 C. 0.6米 D. 2.2米
11、如图,小杰设计用手电 ( http: / / www.21cnjy.com )来测量某古城墙高度,点P处平放一平面镜,光线从点A经过平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,测得AB=1.2m,BP=1.8m,PD=12m,那么古城墙CD的高度是( )m.
A. 6 B. 10 C. 8 D. 12
12、如图,小利在测量学校旗杆高度时, ( http: / / www.21cnjy.com )将3米长的标杆插在离旗杆8米的地方,已知旗杆高度为6米,小利眼部以下距地面1.5米,当小利可以看到标杆顶端与旗杆顶端重合时,他站的地方离旗杆的距离为( )米。
A. 10 B. 11 C. 12 D. 14
13、在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为,把△EFO缩小,则点E的对应点的坐标是( )
A.(-2,1) B.(-8,4) C.(-8,4)或(8,-4) D.(-2,1)或(2,-1)
14、如图,在△ABC中,CD⊥AB于D,图中相似的三角形共有( )对。
A. 1 B. 2 C. 3 D. 4
在△ABC中,∠C是直角,∠A,∠B,∠C,的对边分别是a,b,c,下列式子成立的是( )
A. B. C. D.
16、在△ABC中,∠C是直角,cosA=,则tanB等于( )
A. B. C. D.
17、如图,在△ABC中,CD⊥AB于D,已知AC=8,BC=4,那么tan∠BCD等于( )
A. 1 B. C. D.
18、如图所示,已知点P的坐标是(4,3),则等于( )
A. B. C. D.
19、若菱形ABCD的周长为24cm,面积为18cm2 ,则菱形的最小锐角是( )
A. 30° B. 45° C. 60° D. 90°
20、如图,作等腰直角三角形ABC,∠C=90°,延长边CA到D,使AD=AB,连接DB.利用此图可以求出22.5°的正切值为。利用这种方法你能求出tan75°=( )
A. B. C. D.
填空题(每题3分,共12分)
21、如图,正方形ABCD的边长为1,
P是CD的中点,PQ⊥AP,
则BQ= 。
在△ABC中,D、E分别是AB、AC上的点,
DE∥BC,且DE平分△ABC的面积,
则DE∶BC等于 。
23、一架梯子斜靠在墙上,梯子顶端到地面的距离是3.2米,底端到墙根的距
离是2.4米,如果把梯子的底端到墙根的距离减少0.4米,那么梯子与地面的
夹角是 度。
如图,∠AOB是放置在正方形网格中的一个角,
则cos∠AOB的值是 。
宁阳第二实验中学第一次阶段性考试
初三数学试题卷二
得分:
二 三 总分
25 26 27 28 29
二、填空题(每题3分,共12分)
21 22 23 24
三、解答题(共48分)
25、(16分)
(1)sin30°+ cos60° (2)tan30°·tan60°
(3)sin245°+ cos245° (4)cos30°- sin60°+ tan45°
26、(8)如图所示,在矩形ABCD中,E为BC边上一点,DF⊥AE于F。
(1)△EAB与△ADF相似吗?请说明理由。
(2)若AB=6,AD=12,BE=8,求DF的长
27、(6分)如图,海中有一个小岛 ( http: / / www.21cnjy.com )P,它的周围18海里内有暗礁,渔船跟踪鱼群由西往东航行,在点A测得小岛P在北偏东60°方向上,航行12海里到达B点,这时测得小岛P在北偏东45°方向上。如果渔船不改变航线继续向东航行,有没有触礁的危险?请说明理由。
28、(8分)住宅的采光是建楼和购 ( http: / / www.21cnjy.com )房时人们所关心的问题之一。如图,住宅小区南、北两栋楼的高度均为16.8米,已知当地冬至这天中午12时太阳光线与地面所成的角是35°。
(sin35°=0.6 ,cos35°=0.8,tan35°=0.7)
要使这时南楼的影子恰好落在北楼的墙脚,两楼之间的距离应为多少米?
如果两栋楼房之间的距离为20米,那么这时南楼的影子是否会影响北楼一楼的采光?
29、(10分)某工厂有许多直角边分别为30cm和40cm的直角三角
形下脚料铁皮,要利用它们分别裁剪一个正方形,用来焊接棱长为
17cm的正方体开关盒,有两种方法:一种是正方形的一边在直角三
角形的斜边上,另两个顶点在两条直角边上,如图 ( http: / / www.21cnjy.com )(1);另一种是一组邻边在直角三角形的两直角边上,另一个顶点在斜边上,如图(2).问哪种方式合乎要求?
班级: 姓名: 考号:
初三数学试题卷一
选择题(每题3分,共60分)
下列多边形一定相似的为( )
A. 两个矩形 B. 两个菱形
C. 两个正方形 D. 两个平行四边形
2、若如图所示的两个四边形相似,则∠α的度数是( )
A. 87° B. 60° C. 75° D. 120°
3、如图,点F是□ABCD的边BD上一点,直线BF交AD的延长线于点E,则下列结论错误的是( )
A. B. C. D.
4、如图,BC∥DE,AB=15,AC=9,BD=4则AE=( )
A.6 B.2.4 C.9 D.11.4
5、能判定△ABC与△相似的条件是( )A. B.
C. D.
6、如图,小正方形的边长均为1,则下图中的三角形
(阴影部分)与△ABC相似的为( )
7、如图,P是Rt△ABC的斜边BC上异 ( http: / / www.21cnjy.com )于B、C的一点,过P点作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有( )。
A. 1条 B. 2条 C. 3 条 D. 4条
8、一张矩形报纸ABCD的长AB=acm, ( http: / / www.21cnjy.com )宽BC=bcm,E、F分别是AB,CD的中点,将这张报纸长边的中垂线对折后,矩形AEFD的长与宽之比等于矩形ABCD的长与宽之比,则a:b等于( )
A. B. C. D.
9、如图,D为△ABC的边AB上一点,且∠ABC=∠ACD,AD=4,AB=9,则AC的长为( )
A. 2 B. 5 C. 6 D. 12
10、小明身高1.7米,测得他站立在阳光下 ( http: / / www.21cnjy.com )的影子长为0.85米,紧接着他把手臂竖直举起,测得影子长为1.1米,那么小明举起的手臂超过头顶( )。
A. 0.5米 B. 0.55米 C. 0.6米 D. 2.2米
11、如图,小杰设计用手电 ( http: / / www.21cnjy.com )来测量某古城墙高度,点P处平放一平面镜,光线从点A经过平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,测得AB=1.2m,BP=1.8m,PD=12m,那么古城墙CD的高度是( )m.
A. 6 B. 10 C. 8 D. 12
12、如图,小利在测量学校旗杆高度时, ( http: / / www.21cnjy.com )将3米长的标杆插在离旗杆8米的地方,已知旗杆高度为6米,小利眼部以下距地面1.5米,当小利可以看到标杆顶端与旗杆顶端重合时,他站的地方离旗杆的距离为( )米。
A. 10 B. 11 C. 12 D. 14
13、在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为,把△EFO缩小,则点E的对应点的坐标是( )
A.(-2,1) B.(-8,4) C.(-8,4)或(8,-4) D.(-2,1)或(2,-1)
14、如图,在△ABC中,CD⊥AB于D,图中相似的三角形共有( )对。
A. 1 B. 2 C. 3 D. 4
在△ABC中,∠C是直角,∠A,∠B,∠C,的对边分别是a,b,c,下列式子成立的是( )
A. B. C. D.
16、在△ABC中,∠C是直角,cosA=,则tanB等于( )
A. B. C. D.
17、如图,在△ABC中,CD⊥AB于D,已知AC=8,BC=4,那么tan∠BCD等于( )
A. 1 B. C. D.
18、如图所示,已知点P的坐标是(4,3),则等于( )
A. B. C. D.
19、若菱形ABCD的周长为24cm,面积为18cm2 ,则菱形的最小锐角是( )
A. 30° B. 45° C. 60° D. 90°
20、如图,作等腰直角三角形ABC,∠C=90°,延长边CA到D,使AD=AB,连接DB.利用此图可以求出22.5°的正切值为。利用这种方法你能求出tan75°=( )
A. B. C. D.
填空题(每题3分,共12分)
21、如图,正方形ABCD的边长为1,
P是CD的中点,PQ⊥AP,
则BQ= 。
在△ABC中,D、E分别是AB、AC上的点,
DE∥BC,且DE平分△ABC的面积,
则DE∶BC等于 。
23、一架梯子斜靠在墙上,梯子顶端到地面的距离是3.2米,底端到墙根的距
离是2.4米,如果把梯子的底端到墙根的距离减少0.4米,那么梯子与地面的
夹角是 度。
如图,∠AOB是放置在正方形网格中的一个角,
则cos∠AOB的值是 。
宁阳第二实验中学第一次阶段性考试
初三数学试题卷二
得分:
二 三 总分
25 26 27 28 29
二、填空题(每题3分,共12分)
21 22 23 24
三、解答题(共48分)
25、(16分)
(1)sin30°+ cos60° (2)tan30°·tan60°
(3)sin245°+ cos245° (4)cos30°- sin60°+ tan45°
26、(8)如图所示,在矩形ABCD中,E为BC边上一点,DF⊥AE于F。
(1)△EAB与△ADF相似吗?请说明理由。
(2)若AB=6,AD=12,BE=8,求DF的长
27、(6分)如图,海中有一个小岛 ( http: / / www.21cnjy.com )P,它的周围18海里内有暗礁,渔船跟踪鱼群由西往东航行,在点A测得小岛P在北偏东60°方向上,航行12海里到达B点,这时测得小岛P在北偏东45°方向上。如果渔船不改变航线继续向东航行,有没有触礁的危险?请说明理由。
28、(8分)住宅的采光是建楼和购 ( http: / / www.21cnjy.com )房时人们所关心的问题之一。如图,住宅小区南、北两栋楼的高度均为16.8米,已知当地冬至这天中午12时太阳光线与地面所成的角是35°。
(sin35°=0.6 ,cos35°=0.8,tan35°=0.7)
要使这时南楼的影子恰好落在北楼的墙脚,两楼之间的距离应为多少米?
如果两栋楼房之间的距离为20米,那么这时南楼的影子是否会影响北楼一楼的采光?
29、(10分)某工厂有许多直角边分别为30cm和40cm的直角三角
形下脚料铁皮,要利用它们分别裁剪一个正方形,用来焊接棱长为
17cm的正方体开关盒,有两种方法:一种是正方形的一边在直角三
角形的斜边上,另两个顶点在两条直角边上,如图 ( http: / / www.21cnjy.com )(1);另一种是一组邻边在直角三角形的两直角边上,另一个顶点在斜边上,如图(2).问哪种方式合乎要求?
班级: 姓名: 考号:
同课章节目录
