顺德 角平分线[下学期]
图片预览


文档简介
课件16张PPT。感谢各位老师、专家
莅临指导
角平分线九年级数学备课组驶向成功的彼岸角平分线的性质是什么
用纸剪一个角,把纸片对折,使角的两边叠合在一起,再把纸片展开,你看到了什么?
角平分线上的点到这个角的两边的距离相等? 角平分线的这条性质是怎样得到的呢?把对折的纸片继续任意折一次,然后把纸片展开,你又看到了什么?
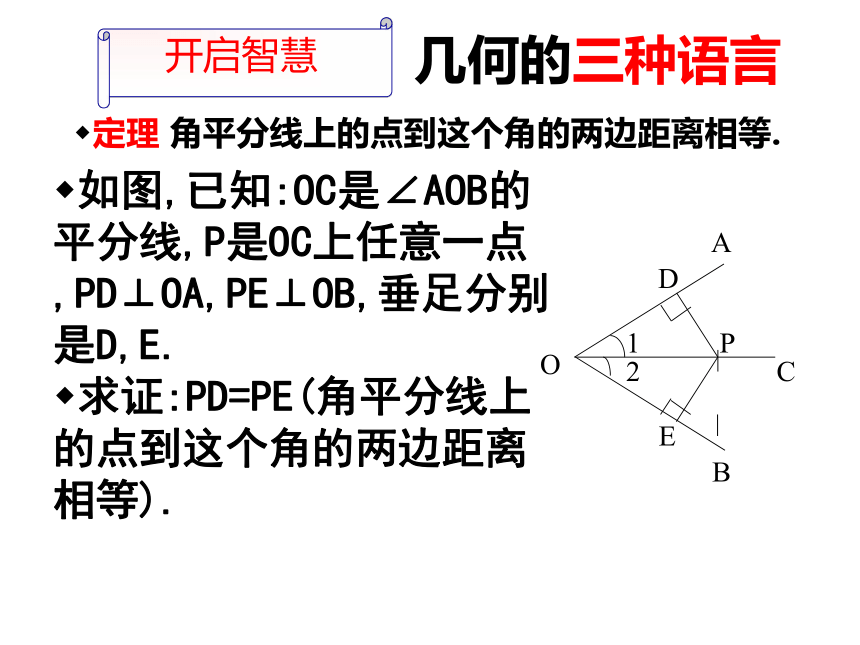
开启智慧几何的三种语言定理 角平分线上的点到这个角的两边距离相等.
如图,已知:OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别是D,E.
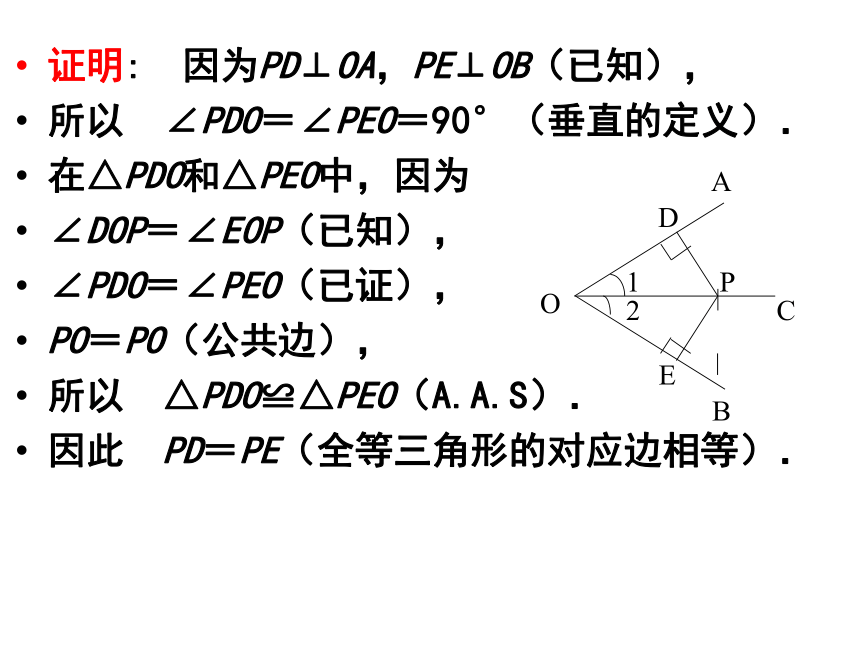
求证:PD=PE(角平分线上的点到这个角的两边距离相等).证明: 因为PD⊥OA,PE⊥OB(已知),
所以 ∠PDO=∠PEO=90°(垂直的定义).
在△PDO和△PEO中,因为
∠DOP=∠EOP(已知),
∠PDO=∠PEO(已证),
PO=PO(公共边),
所以 △PDO≌△PEO(A.A.S).
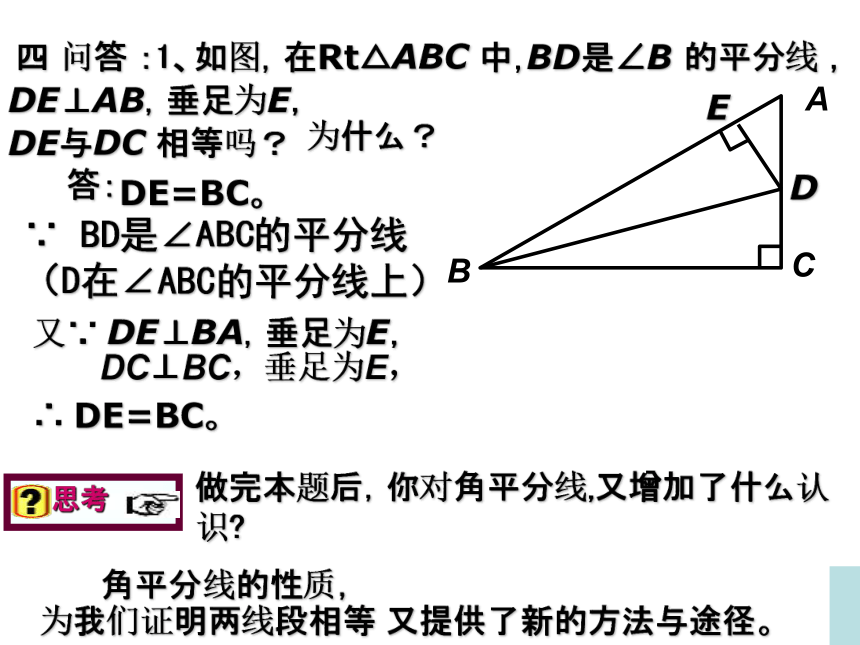
因此 PD=PE(全等三角形的对应边相等).四 问答 :1、如图,在Rt△ABC 中, 角平分线的性质,
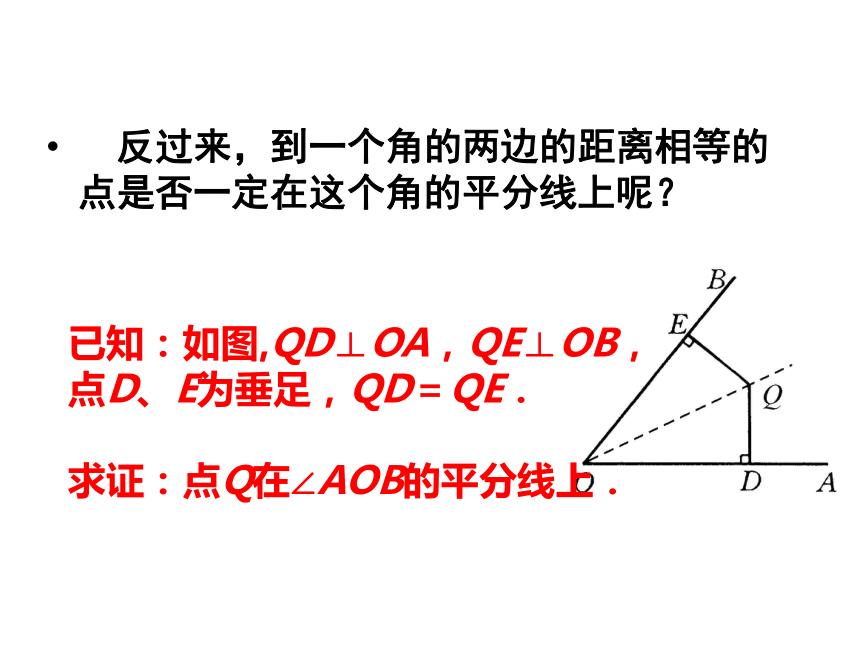
为我们证明两线段相等 又提供了新的方法与途径。ABCBD是∠B 的平分线 ,DE⊥AB,垂足为E,EDE与DC 相等吗?答:DE=BC。∵ BD是∠ABC的平分线 (D在∠ABC的平分线上) 又∵ DE⊥BA,垂足为E,∴ DE=BC。为什么?DC⊥BC,垂足为E, 反过来,到一个角的两边的距离相等的点是否一定在这个角的平分线上呢? 已知:如图,QD⊥OA,QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.命题:三角形三个角的平分线相交于一点.如图,设△ABC的角平分线BM,CN相交于点P,过点P分别作BC,AC,AB的垂线,垂足分别是E,F,D.∵BM是△ABC的角平分线,点P在BM上,∴△ABC的三条角平分线相交于一点P.基本想法是这样的:我们知道,两条直线相交只有一个交点.要想证明三条直线相交于一点,只要能证明两条直线的交点在第三条直线上即可.这时可以考虑前面刚刚学习的内容.∴PD=PE(角平分线上的点到这个角的两边距离相等).同理,PE=PF.∴PD=PF.∴点P在∠BAC的平分线上(在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上).1.(2004·四川)如图,已知点C是∠AOB平分线上一点,点P、P'分别在边OA、OB上。如果要得到PO=OP' ,需要添加以下条件中的某一个即可,请你写出所有可能结果的序号 。
① ∠ OCP= ∠OCP' ;② ∠ OPC= ∠OP' C ;
③PC=PC ' ;④PP' ⊥OC课时训练①或②或④
1、 ∵∠1= ∠2,DC⊥AC, DE⊥AB
∴___________
(___________________________________________)
DC=DE角平分线上的点到角的两边的距离相等2、判断题( )
∵ 如图,AD平分∠BAC(已知) ∴ BD = DC ,
( ) 角的平分线上的点到角的两边的距离相等。× 2.(2004·河北省)如图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入的球袋是 ( )
A.1号袋 B.2号袋 C.3号袋 D.4号袋B3.(2004·广州)如图,CB、CD分别是钝角△AEC和锐角△ABC的中线,且AC=AB,给出下列结论①AE=2AC;②CE=2CD;③ ∠ACD=∠BCE; ④CB平分∠DCE。请写出正确结论的序号 。①②④ 如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
解:设要截取的长度为Xm,则: 要在S区建一个集贸市场,使它到公路和铁路距离相等,且离公路和铁路的交叉处500米,该集贸市场应建在何处?(比例尺 1:20 000)解得:X=0.025m
=2.5cmA则点A即为所求的点2:如图所示, △ABC中,AB=AC,M为BC中点,MD⊥AB于D,ME⊥AC于E。 求证:MD=ME。3:如图所示,PB⊥AB,PC⊥AC,且PB=PC,D是AP上一点。 求证: ∠BDP= ∠CDP感谢指导再 见
莅临指导
角平分线九年级数学备课组驶向成功的彼岸角平分线的性质是什么
用纸剪一个角,把纸片对折,使角的两边叠合在一起,再把纸片展开,你看到了什么?
角平分线上的点到这个角的两边的距离相等? 角平分线的这条性质是怎样得到的呢?把对折的纸片继续任意折一次,然后把纸片展开,你又看到了什么?
开启智慧几何的三种语言定理 角平分线上的点到这个角的两边距离相等.
如图,已知:OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别是D,E.
求证:PD=PE(角平分线上的点到这个角的两边距离相等).证明: 因为PD⊥OA,PE⊥OB(已知),
所以 ∠PDO=∠PEO=90°(垂直的定义).
在△PDO和△PEO中,因为
∠DOP=∠EOP(已知),
∠PDO=∠PEO(已证),
PO=PO(公共边),
所以 △PDO≌△PEO(A.A.S).
因此 PD=PE(全等三角形的对应边相等).四 问答 :1、如图,在Rt△ABC 中, 角平分线的性质,
为我们证明两线段相等 又提供了新的方法与途径。ABCBD是∠B 的平分线 ,DE⊥AB,垂足为E,EDE与DC 相等吗?答:DE=BC。∵ BD是∠ABC的平分线 (D在∠ABC的平分线上) 又∵ DE⊥BA,垂足为E,∴ DE=BC。为什么?DC⊥BC,垂足为E, 反过来,到一个角的两边的距离相等的点是否一定在这个角的平分线上呢? 已知:如图,QD⊥OA,QE⊥OB,
点D、E为垂足,QD=QE.
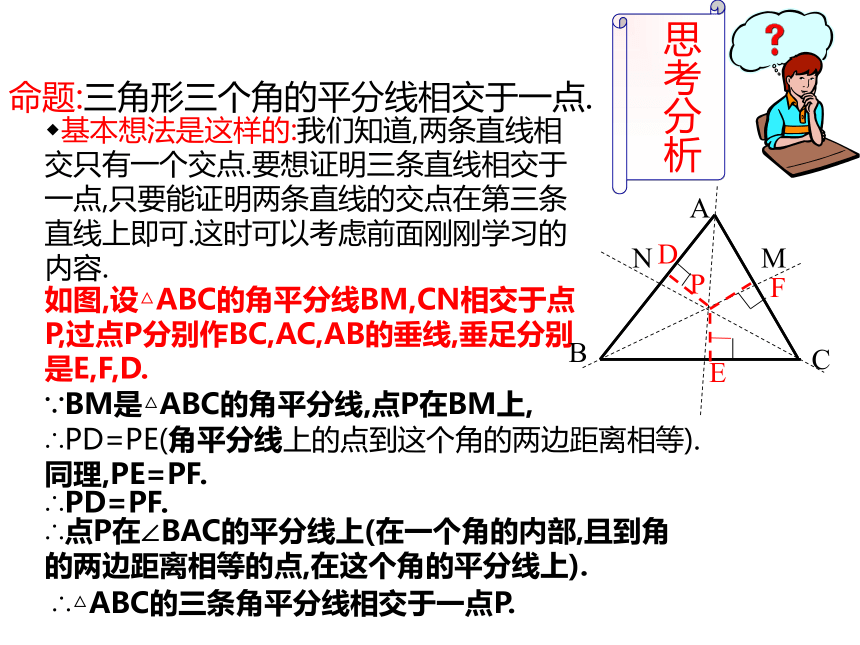
求证:点Q在∠AOB的平分线上.命题:三角形三个角的平分线相交于一点.如图,设△ABC的角平分线BM,CN相交于点P,过点P分别作BC,AC,AB的垂线,垂足分别是E,F,D.∵BM是△ABC的角平分线,点P在BM上,∴△ABC的三条角平分线相交于一点P.基本想法是这样的:我们知道,两条直线相交只有一个交点.要想证明三条直线相交于一点,只要能证明两条直线的交点在第三条直线上即可.这时可以考虑前面刚刚学习的内容.∴PD=PE(角平分线上的点到这个角的两边距离相等).同理,PE=PF.∴PD=PF.∴点P在∠BAC的平分线上(在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上).1.(2004·四川)如图,已知点C是∠AOB平分线上一点,点P、P'分别在边OA、OB上。如果要得到PO=OP' ,需要添加以下条件中的某一个即可,请你写出所有可能结果的序号 。
① ∠ OCP= ∠OCP' ;② ∠ OPC= ∠OP' C ;
③PC=PC ' ;④PP' ⊥OC课时训练①或②或④
1、 ∵∠1= ∠2,DC⊥AC, DE⊥AB
∴___________
(___________________________________________)
DC=DE角平分线上的点到角的两边的距离相等2、判断题( )
∵ 如图,AD平分∠BAC(已知) ∴ BD = DC ,
( ) 角的平分线上的点到角的两边的距离相等。× 2.(2004·河北省)如图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入的球袋是 ( )
A.1号袋 B.2号袋 C.3号袋 D.4号袋B3.(2004·广州)如图,CB、CD分别是钝角△AEC和锐角△ABC的中线,且AC=AB,给出下列结论①AE=2AC;②CE=2CD;③ ∠ACD=∠BCE; ④CB平分∠DCE。请写出正确结论的序号 。①②④ 如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
解:设要截取的长度为Xm,则: 要在S区建一个集贸市场,使它到公路和铁路距离相等,且离公路和铁路的交叉处500米,该集贸市场应建在何处?(比例尺 1:20 000)解得:X=0.025m
=2.5cmA则点A即为所求的点2:如图所示, △ABC中,AB=AC,M为BC中点,MD⊥AB于D,ME⊥AC于E。 求证:MD=ME。3:如图所示,PB⊥AB,PC⊥AC,且PB=PC,D是AP上一点。 求证: ∠BDP= ∠CDP感谢指导再 见
同课章节目录
