1.2.1 矩形的性质与判定 课件(23张PPT)
文档属性
| 名称 | 1.2.1 矩形的性质与判定 课件(23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 09:09:40 | ||
图片预览






文档简介
(共23张PPT)
第一章 特殊平行四边形
第2节 矩形的性质与判定(一)
1.理解矩形的概念,知道矩形与平行四边形的区别与联系。
2.会证明矩形的性质,会用矩形的性质解决简单的问题(重点)
3.应用矩形的性质定理解决相关问题(难点)
情境&导入
观察下面图形,长方形在生活中无处不在.
情境&导入
下面图片中都含有一些特殊的平行四边形.观察这些特殊的平行四边形,你能发现它们有什么样的共同特征?
思考 长方形跟我们前面学行四边形有什么关系?
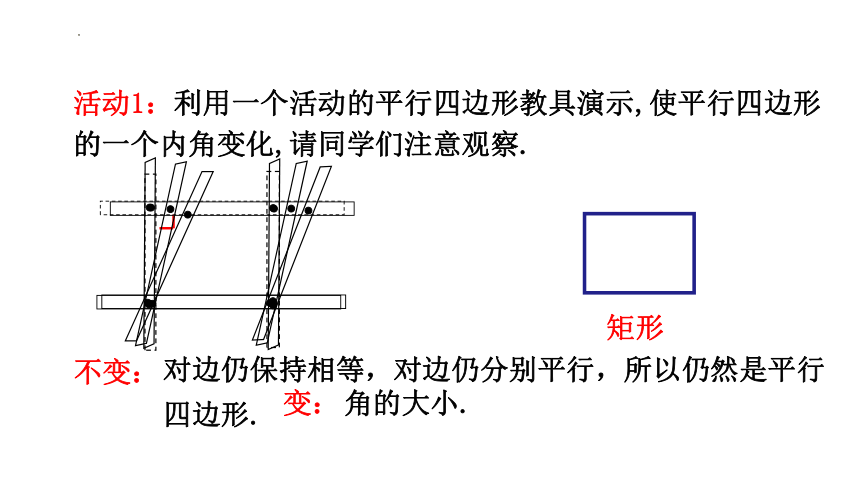
活动1:利用一个活动的平行四边形教具演示,使平行四边形的一个内角变化,请同学们注意观察.
矩形
不变:
变:
对边仍保持相等,对边仍分别平行,所以仍然是平行四边形.
角的大小.
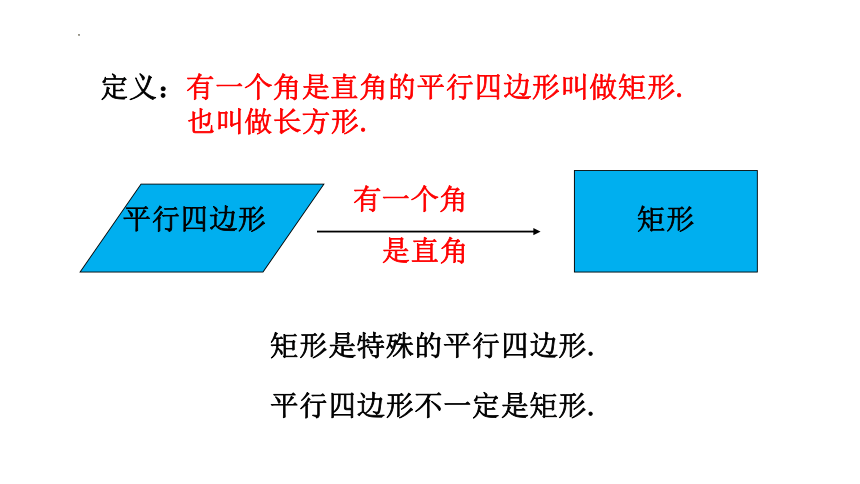
平行四边形
矩形
有一个角
是直角
矩形是特殊的平行四边形.
定义:有一个角是直角的平行四边形叫做矩形.
也叫做长方形.
平行四边形不一定是矩形.
思考 (1)因为矩形是平行四边形,所以它具有平行四边形的所有性质,由于它有一个角为直角,它是否具有一般平行四边形不具有的一些特殊性质呢?
可以从边,角,对角线等方面来考虑.
性质 边 角 对角线 对称性
矩形
对边平行且相等
对角相等
对角线互相平分
中心对称图形
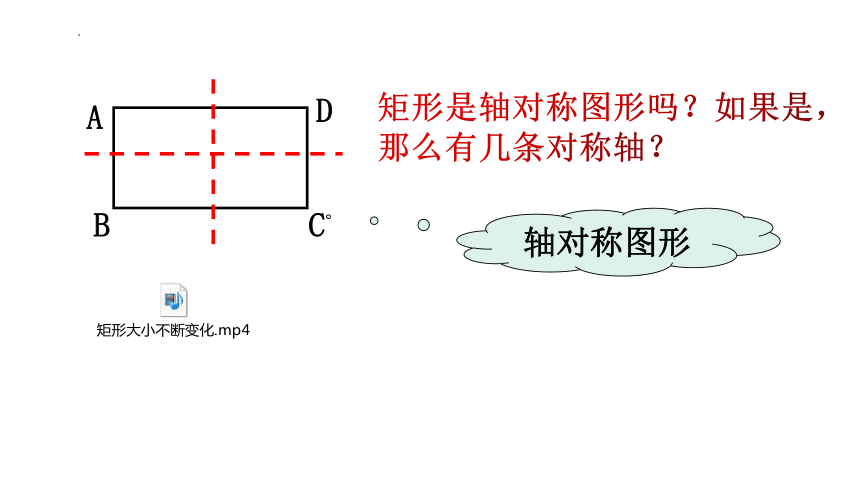
(2)矩形是轴对称图形吗?如果是,它有几条对称轴?
(3)你认为矩形还具有哪些特殊的性质?与同伴交流.
D
C
B
A
矩形是轴对称图形吗?如果是,那么有几条对称轴?
轴对称图形
已知:如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与DB 相交于点O.
求证:∠ABC=∠BCD=∠CDA=∠DAB=90°;
证明:∵四边形ABCD是矩形,
∴∠ABC=∠CDA,∠BCD=∠DAB(矩形的对角相等),AB∥DC(矩形的对边平行).
∴∠ABC+∠BCD=180°.又∵∠ABC=90°,∴∠BCD=90°.
∴∠ABC=∠BCD=∠CDA=∠DAB=90°.
已知:如图,四边形ABCD是矩形,∠ABC= 90°,对角线AC与DB相交于点 O。
求证:AC = BD.
证明:∵四边形 ABCD 是矩形,
∴AB = DC(矩形的对边相等),
在△ABC 和 △DCB 中,
∵AB = DC,∠ABC = ∠DCB,BC = CB.
∴△ABC ≌∠DCB.∴AC = DB.
矩形除了具有平行四边形所有性质,还具有的性质有:
矩形的四个角都是直角.
矩形的对角线相等.
归纳总结
几何语言描述:
在矩形ABCD中,对角线AC与DB相交于点O.
∠ABC=∠BCD=∠CDA=∠DAB =90°,AC=DB.
A
B
C
D
O
例1.如图1-2-1,在 ABCD 中,点E,F 为BC 边上的点,
且BE=CF,AF=DE. 求证: ABCD 是矩形.
证明:∵四边形ABCD 是平行四边形,
∴ AB=CD,∠ B+ ∠ C = 180°.
∵ BE=CF, ∴ BE+EF=CF+EF, 即BF=CE.
又∵ AF=DE,
∴△ ABF ≌△ DCE(SSS).
∴∠ B= ∠ C=90°.
∴ ABCD 是矩形.
请同学们拿出准备好的矩形纸片,折一折,观察并思考。
(1)矩形是不是中心对称图形? 如果是,那么对称中心是什么?
(2)矩形是不是轴对称图形?如果是,那么对称轴有几条?
矩形是中心对称图形,对称中心是对角线的交点
矩形是轴对称图形,它有两条对称轴。
矩形的对边平行且相等.
角
对角线
边
矩形的对角线相等.
矩形的对角线互相平分.
矩形的四个角都是直角.
矩形的对角相等.
对称性
矩形是轴对称图形,也是中心对称图形.
归纳总结
(1)矩形的两条对角线可以把矩形分成几个直角三角形?
(2)在直角三角形ABC中,你能找到它的一条特殊线段吗?
(3)你能发现它有什么特殊的性质吗?
(4)你能借助于矩形加以证明吗?
定理:直角三角形斜边的中线等于斜边的一半.
证明:∵四边形 ABCD 是矩形,
∴AB = DC(矩形的对边相等),
∴BE = DE = AE = CE,
在Rt△ABC 中,
AC为斜边,BE 为斜边上中线,
∴BE = AC.
例2 如图,在矩形 ABCD 中,两条对角线相交于点 O,∠AOD = 120°,AB = 2.5,求这个矩形对角线的长.
解:∵四边形 ABCD 是矩形,
∴ AC = BD(矩形的对角线相等)
OA = OC = AC,OB = OD = BD,
∴OA = OD。
∵∠AOD = 120°,
∴∠ODA =∠OAD= (180°-120°)=30°。
∴BD = 2AB = 2×2.5 = 5.
练习&巩固
1.若直角三角形的两条直角边分别5和12,则斜边上的中线长为 ( )
A.13 B.6 C.6.5 D.不能确定
练习&巩固
2.如图,矩形ABCD的两条对角线相交于点O,若
∠ AOD=60°,OB=4,则DC= ______.
练习&巩固
3.如图,在△ ABC中,∠C=2∠B,点D为BC上一点且AD⊥AB,点E 是BD的中点,连接AE.
求证:∠ AEC=∠ C;
边
角
对角线
对称性
矩的两组对边平行
矩形的两组对角相等
矩形的邻角互补
矩形的对角线互相平分且相等
矩
形
矩形是轴对称图形,对称轴是两条对角线的交点
矩形是中心对称图形,对称中心是两条对角线的交点
第一章 特殊平行四边形
第2节 矩形的性质与判定(一)
1.理解矩形的概念,知道矩形与平行四边形的区别与联系。
2.会证明矩形的性质,会用矩形的性质解决简单的问题(重点)
3.应用矩形的性质定理解决相关问题(难点)
情境&导入
观察下面图形,长方形在生活中无处不在.
情境&导入
下面图片中都含有一些特殊的平行四边形.观察这些特殊的平行四边形,你能发现它们有什么样的共同特征?
思考 长方形跟我们前面学行四边形有什么关系?
活动1:利用一个活动的平行四边形教具演示,使平行四边形的一个内角变化,请同学们注意观察.
矩形
不变:
变:
对边仍保持相等,对边仍分别平行,所以仍然是平行四边形.
角的大小.
平行四边形
矩形
有一个角
是直角
矩形是特殊的平行四边形.
定义:有一个角是直角的平行四边形叫做矩形.
也叫做长方形.
平行四边形不一定是矩形.
思考 (1)因为矩形是平行四边形,所以它具有平行四边形的所有性质,由于它有一个角为直角,它是否具有一般平行四边形不具有的一些特殊性质呢?
可以从边,角,对角线等方面来考虑.
性质 边 角 对角线 对称性
矩形
对边平行且相等
对角相等
对角线互相平分
中心对称图形
(2)矩形是轴对称图形吗?如果是,它有几条对称轴?
(3)你认为矩形还具有哪些特殊的性质?与同伴交流.
D
C
B
A
矩形是轴对称图形吗?如果是,那么有几条对称轴?
轴对称图形
已知:如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与DB 相交于点O.
求证:∠ABC=∠BCD=∠CDA=∠DAB=90°;
证明:∵四边形ABCD是矩形,
∴∠ABC=∠CDA,∠BCD=∠DAB(矩形的对角相等),AB∥DC(矩形的对边平行).
∴∠ABC+∠BCD=180°.又∵∠ABC=90°,∴∠BCD=90°.
∴∠ABC=∠BCD=∠CDA=∠DAB=90°.
已知:如图,四边形ABCD是矩形,∠ABC= 90°,对角线AC与DB相交于点 O。
求证:AC = BD.
证明:∵四边形 ABCD 是矩形,
∴AB = DC(矩形的对边相等),
在△ABC 和 △DCB 中,
∵AB = DC,∠ABC = ∠DCB,BC = CB.
∴△ABC ≌∠DCB.∴AC = DB.
矩形除了具有平行四边形所有性质,还具有的性质有:
矩形的四个角都是直角.
矩形的对角线相等.
归纳总结
几何语言描述:
在矩形ABCD中,对角线AC与DB相交于点O.
∠ABC=∠BCD=∠CDA=∠DAB =90°,AC=DB.
A
B
C
D
O
例1.如图1-2-1,在 ABCD 中,点E,F 为BC 边上的点,
且BE=CF,AF=DE. 求证: ABCD 是矩形.
证明:∵四边形ABCD 是平行四边形,
∴ AB=CD,∠ B+ ∠ C = 180°.
∵ BE=CF, ∴ BE+EF=CF+EF, 即BF=CE.
又∵ AF=DE,
∴△ ABF ≌△ DCE(SSS).
∴∠ B= ∠ C=90°.
∴ ABCD 是矩形.
请同学们拿出准备好的矩形纸片,折一折,观察并思考。
(1)矩形是不是中心对称图形? 如果是,那么对称中心是什么?
(2)矩形是不是轴对称图形?如果是,那么对称轴有几条?
矩形是中心对称图形,对称中心是对角线的交点
矩形是轴对称图形,它有两条对称轴。
矩形的对边平行且相等.
角
对角线
边
矩形的对角线相等.
矩形的对角线互相平分.
矩形的四个角都是直角.
矩形的对角相等.
对称性
矩形是轴对称图形,也是中心对称图形.
归纳总结
(1)矩形的两条对角线可以把矩形分成几个直角三角形?
(2)在直角三角形ABC中,你能找到它的一条特殊线段吗?
(3)你能发现它有什么特殊的性质吗?
(4)你能借助于矩形加以证明吗?
定理:直角三角形斜边的中线等于斜边的一半.
证明:∵四边形 ABCD 是矩形,
∴AB = DC(矩形的对边相等),
∴BE = DE = AE = CE,
在Rt△ABC 中,
AC为斜边,BE 为斜边上中线,
∴BE = AC.
例2 如图,在矩形 ABCD 中,两条对角线相交于点 O,∠AOD = 120°,AB = 2.5,求这个矩形对角线的长.
解:∵四边形 ABCD 是矩形,
∴ AC = BD(矩形的对角线相等)
OA = OC = AC,OB = OD = BD,
∴OA = OD。
∵∠AOD = 120°,
∴∠ODA =∠OAD= (180°-120°)=30°。
∴BD = 2AB = 2×2.5 = 5.
练习&巩固
1.若直角三角形的两条直角边分别5和12,则斜边上的中线长为 ( )
A.13 B.6 C.6.5 D.不能确定
练习&巩固
2.如图,矩形ABCD的两条对角线相交于点O,若
∠ AOD=60°,OB=4,则DC= ______.
练习&巩固
3.如图,在△ ABC中,∠C=2∠B,点D为BC上一点且AD⊥AB,点E 是BD的中点,连接AE.
求证:∠ AEC=∠ C;
边
角
对角线
对称性
矩的两组对边平行
矩形的两组对角相等
矩形的邻角互补
矩形的对角线互相平分且相等
矩
形
矩形是轴对称图形,对称轴是两条对角线的交点
矩形是中心对称图形,对称中心是两条对角线的交点
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
