1.3 探索三角形全等的条件(第5课时) 课件(28张PPT)
文档属性
| 名称 | 1.3 探索三角形全等的条件(第5课时) 课件(28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 09:19:41 | ||
图片预览




文档简介
第1章 · 全等三角形
1.3 探索三角形全等的条件
第5课时 SAS,ASA,AAS的综合应用
学习目标
1.进一步掌握“边角边”、“角边角”和“角角边”判定三角形全等;
2.能灵活应用条件判定两个三角形全等,增强说理能力,进一步提高分析、解决问题的能力.
知识回顾
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}内 容
符号语言(书写格式)
两边及其夹角分别相等的两个三角形全等(简写成“边角边”或“SAS”).
两角及其夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”)
两角分别相等且其中一组等角的对边相等的两个三角形全等(简写成“角角边”或“AAS”)
A
B
C
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
∵在△ABC和△DEF中,
????????=????????,?∠????=∠????,?????????=????????.
∴ △ABC ≌ △DEF(SAS).
?
∵在△ABC和△DEF中,
∠????=∠????,?????????=????????,?∠????=∠????.
∴ △ABC ≌ △DEF(ASA).
?
∵在△ABC和△MNP中,
∠????=∠????,?∠????=∠????,?????????=????????.
∴ △ABC ≌ △DEF(AAS).
?
温故知新
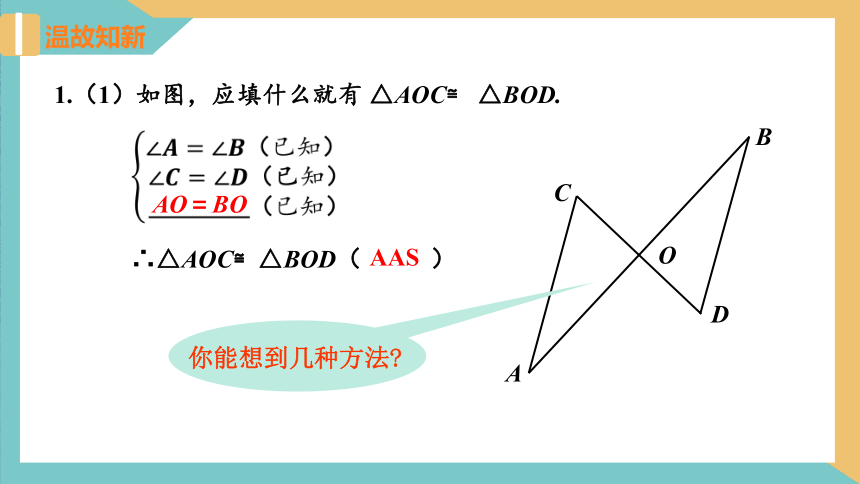
1.(1)如图,应填什么就有 △AOC≌ △BOD.
∠????=∠????(已知)?∠????=∠????(已知)___________(已知)
?
∴△AOC≌△BOD( )
AO=BO
AAS
A
C
B
D
O
你能想到几种方法?
温故知新
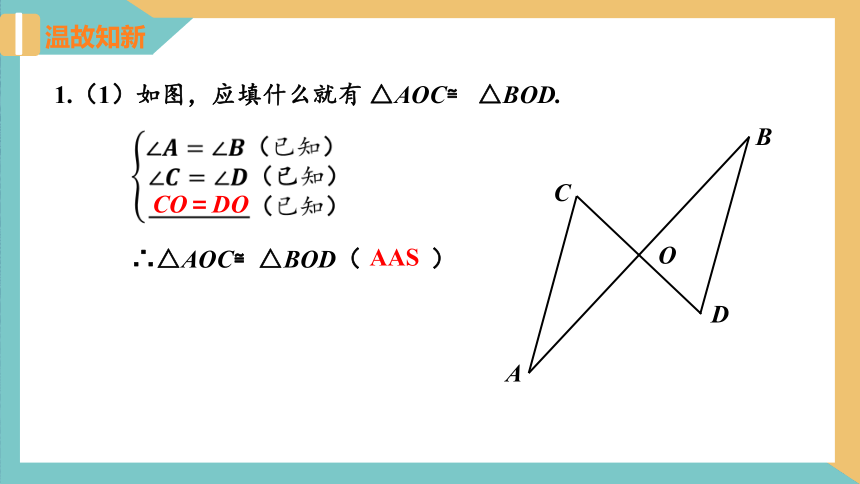
1.(1)如图,应填什么就有 △AOC≌ △BOD.
∠??=∠????(已知)?∠????=∠????(已知)___________(已知)
?
∴△AOC≌△BOD( )
CO=DO
AAS
A
C
B
D
O
温故知新
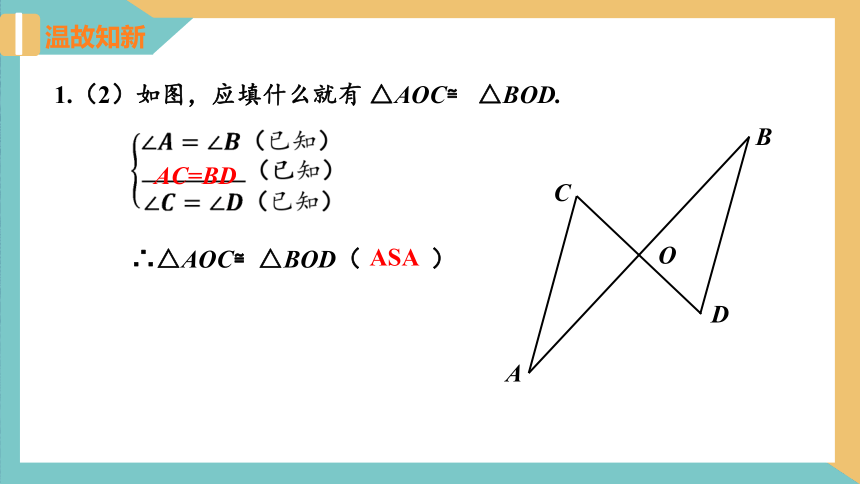
1.(2)如图,应填什么就有 △AOC≌ △BOD.
∠????=∠????(已知)?___________(已知)∠????=∠????(已知)
?
∴△AOC≌△BOD( )
A
C
B
D
O
AC=BD
ASA
温故知新
1.(3)如图,应填什么就有 △AOC≌ △BOD.
??∠????=∠????(已知)?????????=????????(已知)_________________(已知)
?
∴△AOC≌△BOD( )
A
C
B
D
O
∠AOC=∠BOD
ASA
温故知新
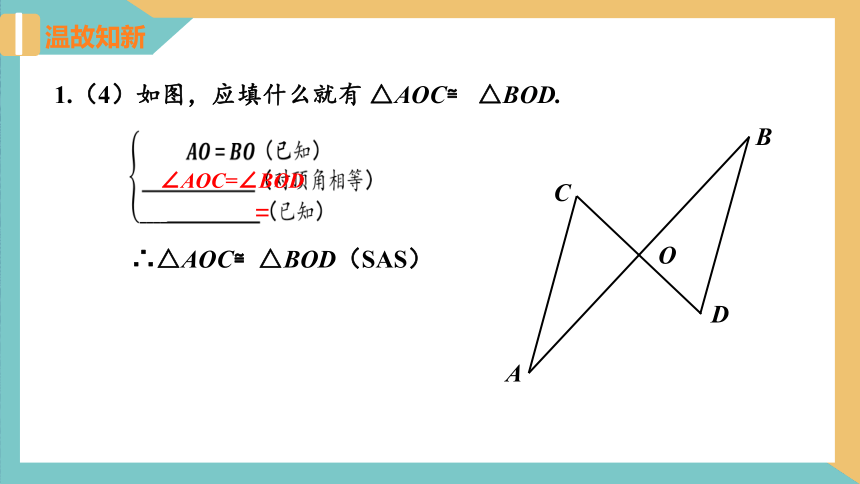
1.(4)如图,应填什么就有 △AOC≌ △BOD.
??????????=????????(已知)??_________________(对顶角相等)__________________(已知)?????????????
?
∴△AOC≌△BOD(SAS)
A
C
B
D
O
∠AOC=∠BOD
????????=????????
复习检测
A
C
B
D
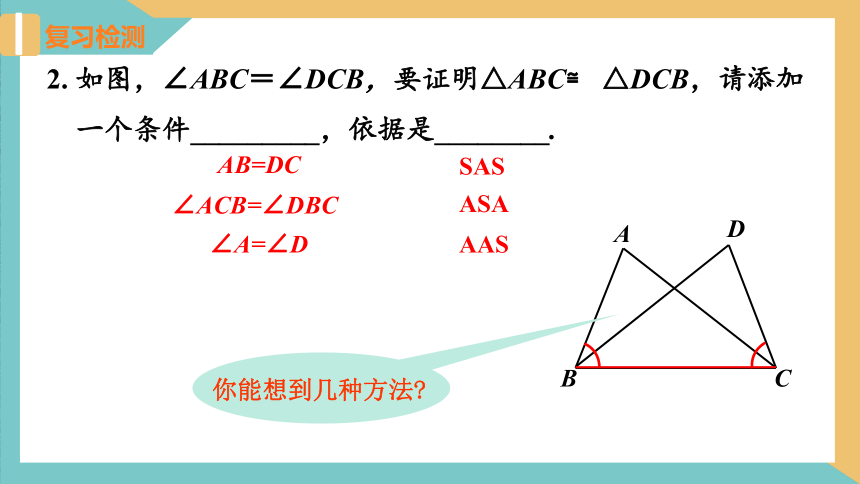
2. 如图,∠ABC=∠DCB,要证明△ABC≌ △DCB,请添加
一个条件_________,依据是________.
你能想到几种方法?
AB=DC
SAS
∠ACB=∠DBC
ASA
∠A=∠D
AAS
方法总结
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}①已知两边
思路1-找夹角
思路2-找第三边
(下一课学习)
②已知两角
思路1-找夹边
思路2-找角的对边
③已知一边一角
思路1-找角的另一组邻边
思路2-找边的另一组邻角
思路3-找边的对角
新知探索
D
B
E
A
C
1
2
1. 如图,∠A=∠B, ∠1=∠2, EA=EB,你能证明AC=BD吗?
证明:∵ ∠1=∠2 (已知),
∴ ∠1+∠BEC=∠2+∠BEC,
∴ ∠AEC=∠BED,
在△EAC和△EBD中,
∠????=∠?????(已知),????????=????????(已知),∠????????????=∠????????????(已证),
∴△EAC≌△EBD(ASA).
∴AC=BD.
?
新知探索
A
D
E
B
C
F
2.如图,点C、F在AD上,且AF=DC,∠B=∠E,∠A=∠D,你能证明AB=DE吗?
证明:∵ AF=DC (已知),
∴ AF -FC=DC-FC,
∴ AC=DF,
在△ABC和△DEF中,
∠????=∠????(已知),∠????=∠????(已知),?????????=????????(已证).?
∴△ABC≌△DEF(AAS),
∴AB=DE(全等三角形对应边相等).
?
AB∥DE
例题讲解
例 已知:如图,点A、B、C、D在一条直线上,EA∥FB,EC∥FD,EA=FB.求证:AB=CD.
F
B
D
E
A
C
证明:∵EA∥FB,EC∥FD(已知),
∴∠A=∠FBD,∠ECA=∠D
(两直线平行,同位角相等).
在△EAC和△FBD中,
∠????=∠????????????(已证),∠????????????=∠????(已证),????????=????????(已知).??
∴△EAC≌△FBD(AAS).
∴AC=BD(全等三角形对应边相等),
即 AB+BC=CD+BC ,
∴AB=CD (等式性质) .
?
例题讲解
上面的推理过程可以用符号“?”简明地表述如下:
证明:EA∥FB?∠A=∠FBD
EC∥FD?∠ECA=∠D ? △EAC≌△FBD
EA=FB
?AC=BD?AB+BC=CD+BC
?AB=CD
新知巩固
1.已知:如图,AB=AC,点D、E分别在AB、AC上,∠B=∠C.
求证:DB=EC .
A
B
C
D
E
O
证明 :在△ABE和△ACF中
∠????=∠????(公共角),???????????=????????(已知),∠????=∠????(已知).???????
?
∴△ABE≌△ACD(ASA),
∴AE=AD(全等三角形对应边相等).
∴AB-AD=AC-AE(等式性质)
即DB=EC.
新知巩固
A
C
B
D
2.已知:如图, ∠ABC=∠DCB,∠1=∠2 ,
求证:AB=DC .
1
2
证明:∵ ∠ABC=∠DCB,∠1=∠2 (已知),
∴ ∠ABC-∠1=∠DCB-∠2 (等式性质),
即∠ACB=∠DBC.
在△ABC和△DCB中,
∠????????????=∠????????????(已知),????????=????????(公共边),∠????????????=∠????????????.?(已证).??
∴△EAC≌△FBD(ASA).
∴AB=DC(全等三角形对应边相等),
?
新知巩固
3. 如图,点A、B、C、D在同一条直线上,EA∥FD,EC∥FB,EA=FD.
求证:AB=CD.
本题推理过程如下:
?△ACE≌△DBF
?AC=DB?AC-BC=DB-BC?AB=CD
请你根据上述推理过程写出完整的证明过程.
A
E
F
C
C
B
新知巩固
A
E
F
C
C
B
证明:∵EA∥FD,EC∥FB,∴∠EAC=∠FDB,∠ECA=∠FBD.
在△ACE和△DBF中,
∠????????????=∠????????????,∠????????????=∠?????????????,????????????=????????.??????????????
∴△ACE≌△DBF(AAS).
∴AC=DB.
∴AC-BC=DB-BC,
即AB=CD.
?
归纳总结
(1)直接条件:即已知中直接给出的三角形的对应边或对应角.
证明三角形全等的“三类条件”:
(2)隐含条件:即已知没有给出,但通过读图得到的条件.
如:公共边、公共角、对顶角、直角相等.
(3)间接条件:即已知中所给条件不是三角形的对应边和对应角,需要
进一步推理.
①等边、等角加(减)等边、等角,其和(差)相等;
②同角或等角的余(补)角相等;
③根据角平分线、平行线得角相等,由中线的定义得边相等.
课堂小结
先确定已知条件
对照判定三角形全等的基本事实和定理
再确定要证明的条件
当堂检测
1.下列说法:
①全等图形的形状相同、大小相等;
②有两边和一角对应相等的两个三角形全等;
③一个锐角和一条直角边对应相等的两个直角三角形全等;
④全等三角形的对应边上的高相等;
其中正确的说法为( )
A.①②④ B.①③④ C.②③④ D.①②③④
B
当堂检测
2. 如图,点B,D,C,F在同一直线上,AC=DE,AC∥DE,添加一个条件,不能得到△ABC≌△EFD的是( )
A.∠B=∠F B.BD=FC C.∠A=∠E D.AB=EF
D
A
C
B
E
F
D
当堂检测
3.如图,填空:(填SAS、ASA或AAS)
(1)已知AD=AE,∠ADB=∠AEC,利用______可以判定△ABD?△ACE;
(2)已知OE=OD,OB=OC,利用______可以判定△BOE?△COD;
(3)已知∠BEC=∠CDB,∠BCE=∠CBD,利用_____可以判定△BCE?△CBD.
A
B
C
D
E
O
ASA
SAS
AAS
当堂检测
4. 2022年冬季奥运会在我国北京举行,奥运健儿们敢于拼搏、善于拼搏,在奥运赛场上展现新时代中国运动员的精神风貌和竞技水平,请你添加一个条件,为奥运健儿设计一只与图1一样的鞋子,已知:AB=DF,∠ABC=∠DFE,写出可添加的条件并标明依据________________.
(三个字母简写理由,写出一种情况即可).
∠????????????=∠????????????
?
当堂检测
5.如图,已知AD平分∠BAC ,AB=AC ,则此图中全等三角形有______对.
A
B
C
E
F
D
提示:根据SAS推出△ABD≌△ACD,求出∠B=∠C,BE=CF,根据全等三角形的判定推出△BDE≌△CDF,△AED≌△AFD,△AFB≌△AEC即可.
4
当堂检测
6. 如图,在△ABC中,∠B=∠C,点D,E,F分别在边AB,BC,AC上,且BD=CE,∠DEF=∠C.请找出图中的全等三角形,并证明你的发现.
A
B
C
E
F
D
解:△BDE≌△CEF.证明如下:
∵∠DEF=∠C,
∠FEB=∠C+∠EFC=∠DEF+∠BED,
∴∠DEB=∠CFE.
在△BDE和△CEF中,
∠????=∠????,∠????????????=∠?????????????,????????????=????????.??????????????
∴△BDE≌△CEF.
?
当堂检测
7. 已知△ABN和△ACM的位置如图,∠1=∠2,AB=AC,AM=AN.
B
N
A
C
M
D
E
1
2
求证:(1)∠M=∠N.
(2)BD=CE.
证明:(1)∵∠1=∠2,
∴∠BAN=∠CAM,
又∵AB=AC,AN=AM,
∴△ABN≌△ACM(SAS),
∴∠M=∠N.
当堂检测
7. 已知△ABN和△ACM的位置如图,∠1=∠2,AB=AC,AM=AN.
B
N
A
C
M
D
E
1
2
求证:(1)∠M=∠N.
(2)BD=CE.
证明:(2)∵△ABN≌△ACM,
∴∠B=∠C,
又∵AB=AC,∠1=∠2,
∴△ABD≌△ACE(ASA),
∴BD=CE.
1.3 探索三角形全等的条件
第5课时 SAS,ASA,AAS的综合应用
学习目标
1.进一步掌握“边角边”、“角边角”和“角角边”判定三角形全等;
2.能灵活应用条件判定两个三角形全等,增强说理能力,进一步提高分析、解决问题的能力.
知识回顾
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}内 容
符号语言(书写格式)
两边及其夹角分别相等的两个三角形全等(简写成“边角边”或“SAS”).
两角及其夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”)
两角分别相等且其中一组等角的对边相等的两个三角形全等(简写成“角角边”或“AAS”)
A
B
C
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
∵在△ABC和△DEF中,
????????=????????,?∠????=∠????,?????????=????????.
∴ △ABC ≌ △DEF(SAS).
?
∵在△ABC和△DEF中,
∠????=∠????,?????????=????????,?∠????=∠????.
∴ △ABC ≌ △DEF(ASA).
?
∵在△ABC和△MNP中,
∠????=∠????,?∠????=∠????,?????????=????????.
∴ △ABC ≌ △DEF(AAS).
?
温故知新
1.(1)如图,应填什么就有 △AOC≌ △BOD.
∠????=∠????(已知)?∠????=∠????(已知)___________(已知)
?
∴△AOC≌△BOD( )
AO=BO
AAS
A
C
B
D
O
你能想到几种方法?
温故知新
1.(1)如图,应填什么就有 △AOC≌ △BOD.
∠??=∠????(已知)?∠????=∠????(已知)___________(已知)
?
∴△AOC≌△BOD( )
CO=DO
AAS
A
C
B
D
O
温故知新
1.(2)如图,应填什么就有 △AOC≌ △BOD.
∠????=∠????(已知)?___________(已知)∠????=∠????(已知)
?
∴△AOC≌△BOD( )
A
C
B
D
O
AC=BD
ASA
温故知新
1.(3)如图,应填什么就有 △AOC≌ △BOD.
??∠????=∠????(已知)?????????=????????(已知)_________________(已知)
?
∴△AOC≌△BOD( )
A
C
B
D
O
∠AOC=∠BOD
ASA
温故知新
1.(4)如图,应填什么就有 △AOC≌ △BOD.
??????????=????????(已知)??_________________(对顶角相等)__________________(已知)?????????????
?
∴△AOC≌△BOD(SAS)
A
C
B
D
O
∠AOC=∠BOD
????????=????????
复习检测
A
C
B
D
2. 如图,∠ABC=∠DCB,要证明△ABC≌ △DCB,请添加
一个条件_________,依据是________.
你能想到几种方法?
AB=DC
SAS
∠ACB=∠DBC
ASA
∠A=∠D
AAS
方法总结
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}①已知两边
思路1-找夹角
思路2-找第三边
(下一课学习)
②已知两角
思路1-找夹边
思路2-找角的对边
③已知一边一角
思路1-找角的另一组邻边
思路2-找边的另一组邻角
思路3-找边的对角
新知探索
D
B
E
A
C
1
2
1. 如图,∠A=∠B, ∠1=∠2, EA=EB,你能证明AC=BD吗?
证明:∵ ∠1=∠2 (已知),
∴ ∠1+∠BEC=∠2+∠BEC,
∴ ∠AEC=∠BED,
在△EAC和△EBD中,
∠????=∠?????(已知),????????=????????(已知),∠????????????=∠????????????(已证),
∴△EAC≌△EBD(ASA).
∴AC=BD.
?
新知探索
A
D
E
B
C
F
2.如图,点C、F在AD上,且AF=DC,∠B=∠E,∠A=∠D,你能证明AB=DE吗?
证明:∵ AF=DC (已知),
∴ AF -FC=DC-FC,
∴ AC=DF,
在△ABC和△DEF中,
∠????=∠????(已知),∠????=∠????(已知),?????????=????????(已证).?
∴△ABC≌△DEF(AAS),
∴AB=DE(全等三角形对应边相等).
?
AB∥DE
例题讲解
例 已知:如图,点A、B、C、D在一条直线上,EA∥FB,EC∥FD,EA=FB.求证:AB=CD.
F
B
D
E
A
C
证明:∵EA∥FB,EC∥FD(已知),
∴∠A=∠FBD,∠ECA=∠D
(两直线平行,同位角相等).
在△EAC和△FBD中,
∠????=∠????????????(已证),∠????????????=∠????(已证),????????=????????(已知).??
∴△EAC≌△FBD(AAS).
∴AC=BD(全等三角形对应边相等),
即 AB+BC=CD+BC ,
∴AB=CD (等式性质) .
?
例题讲解
上面的推理过程可以用符号“?”简明地表述如下:
证明:EA∥FB?∠A=∠FBD
EC∥FD?∠ECA=∠D ? △EAC≌△FBD
EA=FB
?AC=BD?AB+BC=CD+BC
?AB=CD
新知巩固
1.已知:如图,AB=AC,点D、E分别在AB、AC上,∠B=∠C.
求证:DB=EC .
A
B
C
D
E
O
证明 :在△ABE和△ACF中
∠????=∠????(公共角),???????????=????????(已知),∠????=∠????(已知).???????
?
∴△ABE≌△ACD(ASA),
∴AE=AD(全等三角形对应边相等).
∴AB-AD=AC-AE(等式性质)
即DB=EC.
新知巩固
A
C
B
D
2.已知:如图, ∠ABC=∠DCB,∠1=∠2 ,
求证:AB=DC .
1
2
证明:∵ ∠ABC=∠DCB,∠1=∠2 (已知),
∴ ∠ABC-∠1=∠DCB-∠2 (等式性质),
即∠ACB=∠DBC.
在△ABC和△DCB中,
∠????????????=∠????????????(已知),????????=????????(公共边),∠????????????=∠????????????.?(已证).??
∴△EAC≌△FBD(ASA).
∴AB=DC(全等三角形对应边相等),
?
新知巩固
3. 如图,点A、B、C、D在同一条直线上,EA∥FD,EC∥FB,EA=FD.
求证:AB=CD.
本题推理过程如下:
?△ACE≌△DBF
?AC=DB?AC-BC=DB-BC?AB=CD
请你根据上述推理过程写出完整的证明过程.
A
E
F
C
C
B
新知巩固
A
E
F
C
C
B
证明:∵EA∥FD,EC∥FB,∴∠EAC=∠FDB,∠ECA=∠FBD.
在△ACE和△DBF中,
∠????????????=∠????????????,∠????????????=∠?????????????,????????????=????????.??????????????
∴△ACE≌△DBF(AAS).
∴AC=DB.
∴AC-BC=DB-BC,
即AB=CD.
?
归纳总结
(1)直接条件:即已知中直接给出的三角形的对应边或对应角.
证明三角形全等的“三类条件”:
(2)隐含条件:即已知没有给出,但通过读图得到的条件.
如:公共边、公共角、对顶角、直角相等.
(3)间接条件:即已知中所给条件不是三角形的对应边和对应角,需要
进一步推理.
①等边、等角加(减)等边、等角,其和(差)相等;
②同角或等角的余(补)角相等;
③根据角平分线、平行线得角相等,由中线的定义得边相等.
课堂小结
先确定已知条件
对照判定三角形全等的基本事实和定理
再确定要证明的条件
当堂检测
1.下列说法:
①全等图形的形状相同、大小相等;
②有两边和一角对应相等的两个三角形全等;
③一个锐角和一条直角边对应相等的两个直角三角形全等;
④全等三角形的对应边上的高相等;
其中正确的说法为( )
A.①②④ B.①③④ C.②③④ D.①②③④
B
当堂检测
2. 如图,点B,D,C,F在同一直线上,AC=DE,AC∥DE,添加一个条件,不能得到△ABC≌△EFD的是( )
A.∠B=∠F B.BD=FC C.∠A=∠E D.AB=EF
D
A
C
B
E
F
D
当堂检测
3.如图,填空:(填SAS、ASA或AAS)
(1)已知AD=AE,∠ADB=∠AEC,利用______可以判定△ABD?△ACE;
(2)已知OE=OD,OB=OC,利用______可以判定△BOE?△COD;
(3)已知∠BEC=∠CDB,∠BCE=∠CBD,利用_____可以判定△BCE?△CBD.
A
B
C
D
E
O
ASA
SAS
AAS
当堂检测
4. 2022年冬季奥运会在我国北京举行,奥运健儿们敢于拼搏、善于拼搏,在奥运赛场上展现新时代中国运动员的精神风貌和竞技水平,请你添加一个条件,为奥运健儿设计一只与图1一样的鞋子,已知:AB=DF,∠ABC=∠DFE,写出可添加的条件并标明依据________________.
(三个字母简写理由,写出一种情况即可).
∠????????????=∠????????????
?
当堂检测
5.如图,已知AD平分∠BAC ,AB=AC ,则此图中全等三角形有______对.
A
B
C
E
F
D
提示:根据SAS推出△ABD≌△ACD,求出∠B=∠C,BE=CF,根据全等三角形的判定推出△BDE≌△CDF,△AED≌△AFD,△AFB≌△AEC即可.
4
当堂检测
6. 如图,在△ABC中,∠B=∠C,点D,E,F分别在边AB,BC,AC上,且BD=CE,∠DEF=∠C.请找出图中的全等三角形,并证明你的发现.
A
B
C
E
F
D
解:△BDE≌△CEF.证明如下:
∵∠DEF=∠C,
∠FEB=∠C+∠EFC=∠DEF+∠BED,
∴∠DEB=∠CFE.
在△BDE和△CEF中,
∠????=∠????,∠????????????=∠?????????????,????????????=????????.??????????????
∴△BDE≌△CEF.
?
当堂检测
7. 已知△ABN和△ACM的位置如图,∠1=∠2,AB=AC,AM=AN.
B
N
A
C
M
D
E
1
2
求证:(1)∠M=∠N.
(2)BD=CE.
证明:(1)∵∠1=∠2,
∴∠BAN=∠CAM,
又∵AB=AC,AN=AM,
∴△ABN≌△ACM(SAS),
∴∠M=∠N.
当堂检测
7. 已知△ABN和△ACM的位置如图,∠1=∠2,AB=AC,AM=AN.
B
N
A
C
M
D
E
1
2
求证:(1)∠M=∠N.
(2)BD=CE.
证明:(2)∵△ABN≌△ACM,
∴∠B=∠C,
又∵AB=AC,∠1=∠2,
∴△ABD≌△ACE(ASA),
∴BD=CE.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
