1.3 探索三角形全等的条件(第4课时) 课件(27张PPT)
文档属性
| 名称 | 1.3 探索三角形全等的条件(第4课时) 课件(27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 00:00:00 | ||
图片预览







文档简介
第1章 · 全等三角形
1.3 探索三角形全等的条件
第4课时 角角边(AAS)
学习目标
1.探索并掌握两个三角形全等的条件“AAS”;
2.能应用“AAS”判定两个三角形全等,并能运用“AAS”解决简单的实际问题;
3.理解“AAS”与“ASA”之间的联系.
复习回顾
探索3:有三个条件对应相等时
一角和两边
两边和夹角
两边和其中一边的对角
两角和一边
两角和夹边
两角和其中一角的对边
三角
三边
√
×
?
×
√
新知探索
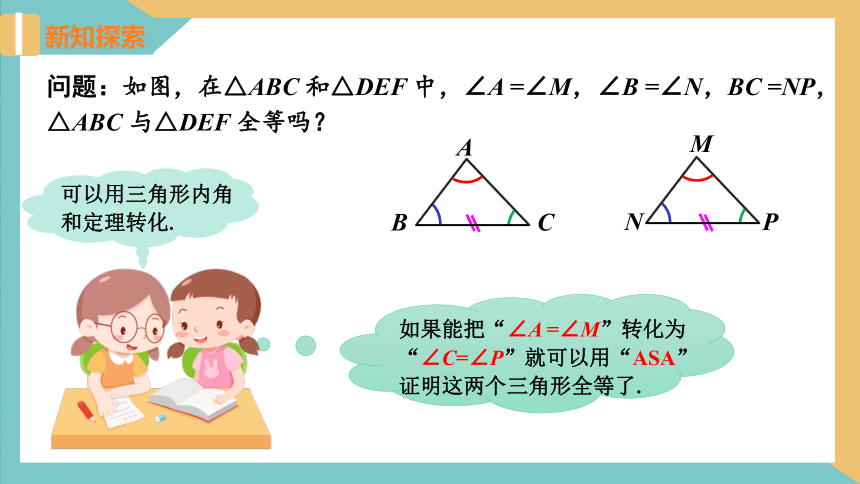
问题:如图,在△ABC 和△DEF 中,∠A =∠M,∠B =∠N,BC =NP,△ABC 与△DEF 全等吗?
如果能把“∠A =∠M”转化为“∠C=∠P”就可以用“ASA”证明这两个三角形全等了.
可以用三角形内角和定理转化.
A
B
C
M
N
P
新知探索
问题:如图,在△ABC 和△DEF 中,∠A =∠M,∠B =∠N,BC =NP,△ABC 与△DEF 全等吗?
证明:
在△ABC中,
∠A+∠B+∠C=180°.
∴△ABC≌△DEF(ASA ).
∴ ∠C=180°-∠A-∠B.
同理 ∠P=180°-∠M-∠N.
又 ∠A=∠M,∠B= ∠N,
∴ ∠C=∠P.
在△ABC和△DEF中,
∠????=∠????,????????=????????,∠????=∠????.
?
M
N
P
A
B
C
新知归纳
角边角的推论:
两角分别相等且其中一组等角的对边相等的两个三角形全等.
(简写成“角角边”或“AAS”)
符号语言:
∵在△ABC和△MNP中,
∠????=∠????,?∠????=∠????,?????????=????????.
∴ △ABC ≌ △MNP(AAS).
?
一组等角的 “对边”
A
B
C
M
N
P
新知应用
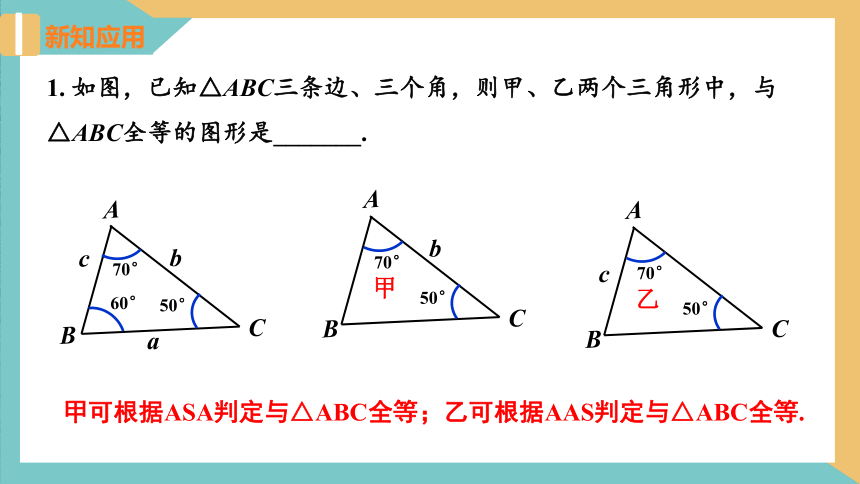
1. 如图,已知△ABC三条边、三个角,则甲、乙两个三角形中,与△ABC全等的图形是_______.
B
A
C
a
60°
50°
b
c
B
A
C
70°
50°
b
甲
B
A
C
70°
50°
c
乙
甲可根据ASA判定与△ABC全等;乙可根据AAS判定与△ABC全等.
70°
新知应用
2. 如图∠ACB=∠DFE,BC=EF,根据“ASA”,应补充一个直接条件___________,根据“AAS”,那么补充的条件为____________,才能使△ABC≌△DEF.
A
C
B
D
F
E
∠B=∠E
∠A=∠D
新知巩固
3. 已知:如图,∠ A=∠D,∠ACB=∠DBC.
求证:AB=DC.
A
B
D
C
证明:在△ABC和△DCB中,
???∠????=∠????(已知),∠????????????=∠????????????(已知),????????=????????(公共边).??
?
∴△ABC≌△DCB(AAS).
∴AB=DC(全等三角形对应边相等).
新知巩固
4.已知:如图,CB⊥AD,AE⊥DC,垂足分别为B、E,AE、BC相交
于点F,且AB=BC.
求证:△ABF≌△CBD.(利用“AAS”)
A
E
D
C
B
F
证明:∵ CB⊥AD,AE⊥DC ,
∴∠ABF=∠CBD =∠AED=90°,
∴∠A+∠AFB=90°, ∠A+∠D=90°.
∴∠AFB=∠D.
在△ABF和△CBD中,
∠????????????=∠????,∠????????????=∠????????????,????????=????????.??
∴△ABF≌△CBD(AAS).
?
新知探索
例1 已知:如图, △ABC≌△ A?B?C? ,AD和A?D?分别是△ABC和△ A?B?C?的高.
求证:AD=A?D? .
A
B
C
D
A′
B′
C′
D′
证明:∵ △ABC≌△ A?B?C? (已知),
∴AB= A?B?,∠B=∠ B?
(全等三角形对应边、对应角相等).
∵ AD、A?D?分别是△ABC和△ A?B?C?的高,
∴ ∠ADB= ∠A?D?B? = 90°.
在△ABD和△ A?B?D?中,
∠????=∠?????(已证),????????????????????????∠????????????=∠????????????????=?????????°(已证),?????????=??????????(已证),??????????????????????????
△ABC≌△ A?B?C?(AAS),
∴AD= A?D? (全等三角形对应边相等).
?
如果AD和A?D?分别是△ABC和△ A?B?C?的角平分线(或中线),那么AD和A?D?相等吗?
试试证明你的结论.
讨论交流
1.已知:如图, △ABC≌△ A?B?C? ,AD和A?D?分别是△ABC和△ A?B?C?的角平分线.
求证:AD=A?D? .
A
B
C
D
A′
B′
C′
D′
证明:∵ △ABC≌△ A?B?C? (已知),
∴AB= A?B?,∠B=∠ B? ,∠BAC=∠B?A? C?
(全等三角形对应边、对应角相等).
∵ AD、A?D?分别是△ABC和△ A?B?C?的角平分线,
∴ ∠BAD= ????????∠BAC,∠B?A? D? = ???????? B?A? C?
(角平分线定义),
∴ ∠BAD= ∠B?A? D? (等量代换) .
在△ABD和△ A?B?D?中,
?∠????=∠?????(已证),????????????????????????????????=??????????(已证),????????????∠????????????=∠????????????????(已证),??
△ABC≌△ A?B?C?(ASA),
∴AD= A?D? (全等三角形对应边相等).
?
讨论交流
A
B
C
D
A′
B′
C′
D′
证明:∵ △ABC≌△ A?B?C? (已知),
∴AB= A?B?,∠B=∠ B? ,BC=B?C?
(全等三角形对应边、对应角相等).
∵ AD、A?D?分别是△ABC和△ A?B?C?的中线,
∴ BD= ????????BC,B?D? = ???????? B? C? (中线定义),
∴ BD= B? D? (等量代换) .
在△ABD和△ A?B?D?中,
????????=??????????(已证),????????????????????????∠????=∠?????(已证),????????????????????????=???????????(已证),?????????????????????
△ABC≌△ A?B?C?(SAS),
∴AD= A?D? (全等三角形对应边相等).
?
延伸:全等三角形对应高、对应角平分线、对应中线相等.
2.已知:如图, △ABC≌△ A?B?C? ,AD和A?D?分别是△ABC和△ A?B?C?的中线.
求证:AD=A?D? .
例题讲解
例2 如图,已知:AB⊥AC ,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.
(1)你能在图中找出一对全等三角形吗?并说明全等的理由.;
解:(1)能, △BDA≌△AEC
∵BD⊥m,CE⊥m,
∴∠ADB=∠CEA=90°,
∴∠ABD+∠BAD=90°.
∵AB⊥AC,
∴∠BAD+∠CAE=90°,
∠ABD=∠CAE.
在△BDA和△AEC中,
∠????=∠????????????,????????=????????,∠????????????=∠????.??
∴△BDA≌△AEC(AAS).
?
A
E
m
C
B
D
例题讲解
例2 如图,已知:AB⊥AC ,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.
(2)试探索BD、CE、DE之间的关系.
∴BD=AE,AD=CE,
∵DE=AD+AE
∴DE=CE+BD.
解:(2)∵△BDA≌△AEC,
A
E
m
C
B
D
课后思考
变式1 (例2) :若B、C在直线m的两侧,其他条件不变,BD、CE、DE三条线段之间满足什么关系?写出你的猜测,并说明你的理由.
A
E
m
C
B
D
∴BD=AE,AD=CE,
∵DE=AD-AE,
∴DE=CE-BD.
解:∵△BDA≌△AEC(同上),
课后思考
变式2(例2):如果“条件中”的“BD⊥直线m,CE⊥直线m , AB⊥AC”改为“∠BDA=∠AEC=∠BAC”,其他条件不变,请问△BDA与△AEC还全等吗?请说明理由.
B
A
C
E
m
D
解:△BDA≌△AEC;理由如下:
∵∠B+∠BDA+∠DAB=∠DAB+∠BAC+∠CAE=180°,
又∵∠BDA=∠AEC=∠BAC ,
∴∠B=∠CAE,
∵在△ BDA和△ AEC中
???∠????????????=∠????????????,∠????=∠????????????,????????=????????.??
∴△ BDA ≌△ AEC(AAS ).
?
归纳总结
利用全等三角形可以解决线段之间的关系,比如线段的相等关系、和差关系等,解决问题的关键是运用全等三角形的判定与性质进行线段之间的转化.
课堂小结
角角边
内容
应用
全等三角形对应高、中线、角平分线相等.
注意“角角边”、“角边角”中两角与边的区别
当堂检测
1. △ABC和△DEF中,AB=DE,∠B=∠E,要使△ABC≌△DEF ,则下列补充的条件中错误的是( )
A.AC=DF B.BC=EF C.∠A=∠D D.∠C=∠F
A
2. 在△ABC与△A′B′C′中,已知∠A=44°,∠B=67°,∠C′=69°,∠A′=44°,且AC=A′C′,那么这两个三角形( )
A.一定不全等 B.一定全等
C.不一定全等 D.以上都不对
B
当堂检测
3.已知:如图,已知AC平分∠BAD, AB⊥BC,AD⊥DC,可以证明△ABC≌________,依据是____________
A
C
D
B
△ADC
AAS
当堂检测
4.如图,AC=DC,∠ACD=∠BCE,请添加一个已知条件_______________________,使△ABC≌△DEC.
C
E
A
B
D
∠A=∠D(答案不唯一)
当堂检测
5.已知:点D在AB上,点E在AC上,BE和CD相交于点O,AE=AF,∠B=∠C
求证: BF=CE.
A
B
C
F
E
O
证明 :在△ABE和△ACF中
∠????=∠????(公共角),???∠????=∠????(已知),????????=????????(已知).???????
?
∴△ABE≌△ACF(AAS),
∴AB=AC(全等三角形对应边相等).
∵AE=AF(已知),
∴AB-AF=AC-AE(等式性质)
∴BF=CE.
当堂检测
A
E
F
C
B
D
(1)如果AD是△ABC的中线,那么BE与CF相等吗?为什么?
6.已知:如图,在△ABC中,BE⊥AE,CF⊥AE,BE、CF与AE分别交于点E、F.
(1)解:BE与CF相等.理由如下:
∵ AD是△ABC的中线,
∴ BD=CD= ????????BC.(中线定义),
∵ BE⊥AE,CF⊥AE,
∴∠E=∠DFC=90°.
在△BDE和△ CDF中,
∠????=∠????????????(已证),????????????????????????∠????????????=∠????????????(对顶角相等),????????????????????????=????????(已证),?????????????????????
△BDE≌△ CDF(AAS),
∴BE= CF(全等三角形对应边相等).
?
当堂检测
6.已知:如图,在△ABC中,BE⊥AE,CF⊥AE,BE、CF与AE分别交于点E、F.
(2)如果BE=CF,那么AD是△ABC的中线吗?为什么?
A
E
F
C
B
D
(2)解:AD是△ABC的中线.理由如下:
∵ BE⊥AE,CF⊥AE,
∴∠E=∠DFC=90°.
在△BDE和△ CDF中,
∠????=∠????????????(已证),????????????????????????∠????????????=∠????????????(对顶角相等),????????????????????????=????????(已证),?????????????????????
△BDE≌△ CDF(AAS),
∴BD= CD(全等三角形对应边相等).
∴ AD是△ABC的中线(中线定义).
?
当堂检测
7. 如图,∠DCE=90°,CD=CE,DA⊥AC,EB⊥AC,垂足分别为A、B.
(1)求证:△ACD≌△BEC;
解:(1)证明:∵∠DCE=90°,EB⊥AC,
∴∠ECB+∠ACD=90°,∠E+∠ECB=90°.
∴∠ACD=∠E.
∵DA⊥AC,EB⊥AC,
∴∠A=∠EBC=90°.
在△ACD和△BEC中,
???∠????=∠????????????,∠????????????=∠????,????????=????????.??
∴△ACD≌△BEC(AAS).
?
A
E
D
C
B
当堂检测
7. 如图,∠DCE=90°,CD=CE,DA⊥AC,EB⊥AC,垂足分别为A、B.
(2)请通过观察或测量线段AD、AB、BE的长度,猜想线段AD、AB、BE之间的数量关系,并证明你的猜想.
A
E
D
C
B
解:(2)线段AD、AB、BE之间的数量关系是:AD+AB=BE.
证明如下:
∵△ACD≌△BEC,
∴AD=BC,AC=BE.
∴AD+AB=BC+AB=AC.
∴AD+AB=BE.
1.3 探索三角形全等的条件
第4课时 角角边(AAS)
学习目标
1.探索并掌握两个三角形全等的条件“AAS”;
2.能应用“AAS”判定两个三角形全等,并能运用“AAS”解决简单的实际问题;
3.理解“AAS”与“ASA”之间的联系.
复习回顾
探索3:有三个条件对应相等时
一角和两边
两边和夹角
两边和其中一边的对角
两角和一边
两角和夹边
两角和其中一角的对边
三角
三边
√
×
?
×
√
新知探索
问题:如图,在△ABC 和△DEF 中,∠A =∠M,∠B =∠N,BC =NP,△ABC 与△DEF 全等吗?
如果能把“∠A =∠M”转化为“∠C=∠P”就可以用“ASA”证明这两个三角形全等了.
可以用三角形内角和定理转化.
A
B
C
M
N
P
新知探索
问题:如图,在△ABC 和△DEF 中,∠A =∠M,∠B =∠N,BC =NP,△ABC 与△DEF 全等吗?
证明:
在△ABC中,
∠A+∠B+∠C=180°.
∴△ABC≌△DEF(ASA ).
∴ ∠C=180°-∠A-∠B.
同理 ∠P=180°-∠M-∠N.
又 ∠A=∠M,∠B= ∠N,
∴ ∠C=∠P.
在△ABC和△DEF中,
∠????=∠????,????????=????????,∠????=∠????.
?
M
N
P
A
B
C
新知归纳
角边角的推论:
两角分别相等且其中一组等角的对边相等的两个三角形全等.
(简写成“角角边”或“AAS”)
符号语言:
∵在△ABC和△MNP中,
∠????=∠????,?∠????=∠????,?????????=????????.
∴ △ABC ≌ △MNP(AAS).
?
一组等角的 “对边”
A
B
C
M
N
P
新知应用
1. 如图,已知△ABC三条边、三个角,则甲、乙两个三角形中,与△ABC全等的图形是_______.
B
A
C
a
60°
50°
b
c
B
A
C
70°
50°
b
甲
B
A
C
70°
50°
c
乙
甲可根据ASA判定与△ABC全等;乙可根据AAS判定与△ABC全等.
70°
新知应用
2. 如图∠ACB=∠DFE,BC=EF,根据“ASA”,应补充一个直接条件___________,根据“AAS”,那么补充的条件为____________,才能使△ABC≌△DEF.
A
C
B
D
F
E
∠B=∠E
∠A=∠D
新知巩固
3. 已知:如图,∠ A=∠D,∠ACB=∠DBC.
求证:AB=DC.
A
B
D
C
证明:在△ABC和△DCB中,
???∠????=∠????(已知),∠????????????=∠????????????(已知),????????=????????(公共边).??
?
∴△ABC≌△DCB(AAS).
∴AB=DC(全等三角形对应边相等).
新知巩固
4.已知:如图,CB⊥AD,AE⊥DC,垂足分别为B、E,AE、BC相交
于点F,且AB=BC.
求证:△ABF≌△CBD.(利用“AAS”)
A
E
D
C
B
F
证明:∵ CB⊥AD,AE⊥DC ,
∴∠ABF=∠CBD =∠AED=90°,
∴∠A+∠AFB=90°, ∠A+∠D=90°.
∴∠AFB=∠D.
在△ABF和△CBD中,
∠????????????=∠????,∠????????????=∠????????????,????????=????????.??
∴△ABF≌△CBD(AAS).
?
新知探索
例1 已知:如图, △ABC≌△ A?B?C? ,AD和A?D?分别是△ABC和△ A?B?C?的高.
求证:AD=A?D? .
A
B
C
D
A′
B′
C′
D′
证明:∵ △ABC≌△ A?B?C? (已知),
∴AB= A?B?,∠B=∠ B?
(全等三角形对应边、对应角相等).
∵ AD、A?D?分别是△ABC和△ A?B?C?的高,
∴ ∠ADB= ∠A?D?B? = 90°.
在△ABD和△ A?B?D?中,
∠????=∠?????(已证),????????????????????????∠????????????=∠????????????????=?????????°(已证),?????????=??????????(已证),??????????????????????????
△ABC≌△ A?B?C?(AAS),
∴AD= A?D? (全等三角形对应边相等).
?
如果AD和A?D?分别是△ABC和△ A?B?C?的角平分线(或中线),那么AD和A?D?相等吗?
试试证明你的结论.
讨论交流
1.已知:如图, △ABC≌△ A?B?C? ,AD和A?D?分别是△ABC和△ A?B?C?的角平分线.
求证:AD=A?D? .
A
B
C
D
A′
B′
C′
D′
证明:∵ △ABC≌△ A?B?C? (已知),
∴AB= A?B?,∠B=∠ B? ,∠BAC=∠B?A? C?
(全等三角形对应边、对应角相等).
∵ AD、A?D?分别是△ABC和△ A?B?C?的角平分线,
∴ ∠BAD= ????????∠BAC,∠B?A? D? = ???????? B?A? C?
(角平分线定义),
∴ ∠BAD= ∠B?A? D? (等量代换) .
在△ABD和△ A?B?D?中,
?∠????=∠?????(已证),????????????????????????????????=??????????(已证),????????????∠????????????=∠????????????????(已证),??
△ABC≌△ A?B?C?(ASA),
∴AD= A?D? (全等三角形对应边相等).
?
讨论交流
A
B
C
D
A′
B′
C′
D′
证明:∵ △ABC≌△ A?B?C? (已知),
∴AB= A?B?,∠B=∠ B? ,BC=B?C?
(全等三角形对应边、对应角相等).
∵ AD、A?D?分别是△ABC和△ A?B?C?的中线,
∴ BD= ????????BC,B?D? = ???????? B? C? (中线定义),
∴ BD= B? D? (等量代换) .
在△ABD和△ A?B?D?中,
????????=??????????(已证),????????????????????????∠????=∠?????(已证),????????????????????????=???????????(已证),?????????????????????
△ABC≌△ A?B?C?(SAS),
∴AD= A?D? (全等三角形对应边相等).
?
延伸:全等三角形对应高、对应角平分线、对应中线相等.
2.已知:如图, △ABC≌△ A?B?C? ,AD和A?D?分别是△ABC和△ A?B?C?的中线.
求证:AD=A?D? .
例题讲解
例2 如图,已知:AB⊥AC ,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.
(1)你能在图中找出一对全等三角形吗?并说明全等的理由.;
解:(1)能, △BDA≌△AEC
∵BD⊥m,CE⊥m,
∴∠ADB=∠CEA=90°,
∴∠ABD+∠BAD=90°.
∵AB⊥AC,
∴∠BAD+∠CAE=90°,
∠ABD=∠CAE.
在△BDA和△AEC中,
∠????=∠????????????,????????=????????,∠????????????=∠????.??
∴△BDA≌△AEC(AAS).
?
A
E
m
C
B
D
例题讲解
例2 如图,已知:AB⊥AC ,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.
(2)试探索BD、CE、DE之间的关系.
∴BD=AE,AD=CE,
∵DE=AD+AE
∴DE=CE+BD.
解:(2)∵△BDA≌△AEC,
A
E
m
C
B
D
课后思考
变式1 (例2) :若B、C在直线m的两侧,其他条件不变,BD、CE、DE三条线段之间满足什么关系?写出你的猜测,并说明你的理由.
A
E
m
C
B
D
∴BD=AE,AD=CE,
∵DE=AD-AE,
∴DE=CE-BD.
解:∵△BDA≌△AEC(同上),
课后思考
变式2(例2):如果“条件中”的“BD⊥直线m,CE⊥直线m , AB⊥AC”改为“∠BDA=∠AEC=∠BAC”,其他条件不变,请问△BDA与△AEC还全等吗?请说明理由.
B
A
C
E
m
D
解:△BDA≌△AEC;理由如下:
∵∠B+∠BDA+∠DAB=∠DAB+∠BAC+∠CAE=180°,
又∵∠BDA=∠AEC=∠BAC ,
∴∠B=∠CAE,
∵在△ BDA和△ AEC中
???∠????????????=∠????????????,∠????=∠????????????,????????=????????.??
∴△ BDA ≌△ AEC(AAS ).
?
归纳总结
利用全等三角形可以解决线段之间的关系,比如线段的相等关系、和差关系等,解决问题的关键是运用全等三角形的判定与性质进行线段之间的转化.
课堂小结
角角边
内容
应用
全等三角形对应高、中线、角平分线相等.
注意“角角边”、“角边角”中两角与边的区别
当堂检测
1. △ABC和△DEF中,AB=DE,∠B=∠E,要使△ABC≌△DEF ,则下列补充的条件中错误的是( )
A.AC=DF B.BC=EF C.∠A=∠D D.∠C=∠F
A
2. 在△ABC与△A′B′C′中,已知∠A=44°,∠B=67°,∠C′=69°,∠A′=44°,且AC=A′C′,那么这两个三角形( )
A.一定不全等 B.一定全等
C.不一定全等 D.以上都不对
B
当堂检测
3.已知:如图,已知AC平分∠BAD, AB⊥BC,AD⊥DC,可以证明△ABC≌________,依据是____________
A
C
D
B
△ADC
AAS
当堂检测
4.如图,AC=DC,∠ACD=∠BCE,请添加一个已知条件_______________________,使△ABC≌△DEC.
C
E
A
B
D
∠A=∠D(答案不唯一)
当堂检测
5.已知:点D在AB上,点E在AC上,BE和CD相交于点O,AE=AF,∠B=∠C
求证: BF=CE.
A
B
C
F
E
O
证明 :在△ABE和△ACF中
∠????=∠????(公共角),???∠????=∠????(已知),????????=????????(已知).???????
?
∴△ABE≌△ACF(AAS),
∴AB=AC(全等三角形对应边相等).
∵AE=AF(已知),
∴AB-AF=AC-AE(等式性质)
∴BF=CE.
当堂检测
A
E
F
C
B
D
(1)如果AD是△ABC的中线,那么BE与CF相等吗?为什么?
6.已知:如图,在△ABC中,BE⊥AE,CF⊥AE,BE、CF与AE分别交于点E、F.
(1)解:BE与CF相等.理由如下:
∵ AD是△ABC的中线,
∴ BD=CD= ????????BC.(中线定义),
∵ BE⊥AE,CF⊥AE,
∴∠E=∠DFC=90°.
在△BDE和△ CDF中,
∠????=∠????????????(已证),????????????????????????∠????????????=∠????????????(对顶角相等),????????????????????????=????????(已证),?????????????????????
△BDE≌△ CDF(AAS),
∴BE= CF(全等三角形对应边相等).
?
当堂检测
6.已知:如图,在△ABC中,BE⊥AE,CF⊥AE,BE、CF与AE分别交于点E、F.
(2)如果BE=CF,那么AD是△ABC的中线吗?为什么?
A
E
F
C
B
D
(2)解:AD是△ABC的中线.理由如下:
∵ BE⊥AE,CF⊥AE,
∴∠E=∠DFC=90°.
在△BDE和△ CDF中,
∠????=∠????????????(已证),????????????????????????∠????????????=∠????????????(对顶角相等),????????????????????????=????????(已证),?????????????????????
△BDE≌△ CDF(AAS),
∴BD= CD(全等三角形对应边相等).
∴ AD是△ABC的中线(中线定义).
?
当堂检测
7. 如图,∠DCE=90°,CD=CE,DA⊥AC,EB⊥AC,垂足分别为A、B.
(1)求证:△ACD≌△BEC;
解:(1)证明:∵∠DCE=90°,EB⊥AC,
∴∠ECB+∠ACD=90°,∠E+∠ECB=90°.
∴∠ACD=∠E.
∵DA⊥AC,EB⊥AC,
∴∠A=∠EBC=90°.
在△ACD和△BEC中,
???∠????=∠????????????,∠????????????=∠????,????????=????????.??
∴△ACD≌△BEC(AAS).
?
A
E
D
C
B
当堂检测
7. 如图,∠DCE=90°,CD=CE,DA⊥AC,EB⊥AC,垂足分别为A、B.
(2)请通过观察或测量线段AD、AB、BE的长度,猜想线段AD、AB、BE之间的数量关系,并证明你的猜想.
A
E
D
C
B
解:(2)线段AD、AB、BE之间的数量关系是:AD+AB=BE.
证明如下:
∵△ACD≌△BEC,
∴AD=BC,AC=BE.
∴AD+AB=BC+AB=AC.
∴AD+AB=BE.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
