1.4.1有理数的乘法(第二课时) 课件(25张PPT)
文档属性
| 名称 | 1.4.1有理数的乘法(第二课时) 课件(25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
第1章 有理数
1.4.1 有理数的乘法
第一单元
1.掌握有理数乘法的运算律,并利用运算律简化乘法运算. (运算能力)
2掌握乘法的分配律,并能灵活的运用. (运算能力)
一、有理数乘法法则
1.两数相乘,同号得正,异号得负,并把绝对值相乘.
2.任何数同0相乘,都得0.
思考:(1)若a<0,b>0,则ab 0 ;
(2)若a<0,b<0,则ab 0 ;
(3)若ab>0,则a、b应满足什么条件?
(4)若ab<0,则a、b应满足什么条件?
<
>
a、b同号
a、b异号
1.几个非零的数相乘:
几个不是0的数相乘,当负因数的个数是_____时,积是正数;当负因数的个数是_____时,积是负数.
偶数
奇数
二、多个有理数相乘的运算规律
2.几个数相乘,其中含有0:
几个数相乘,如果其中有因数为0,那么积等于0.
4×(-5)=____,(-5)×4=____; 6×(-2)=____,(-2)×6=____;
即
[2×(-3)]×(-5)=__________=____,2×[(-3)×(-5)]=_______=____.
即
-20
-20
4×(-5)=(-5)×4;
6×(-2)=(-2)×6.
-12
-12
(-6)×(-5)
30
2×15
30
[2×(-3)]×(-5)=2×[(-3)×(-5)]
上面每组运算分别体现了什么运算律?
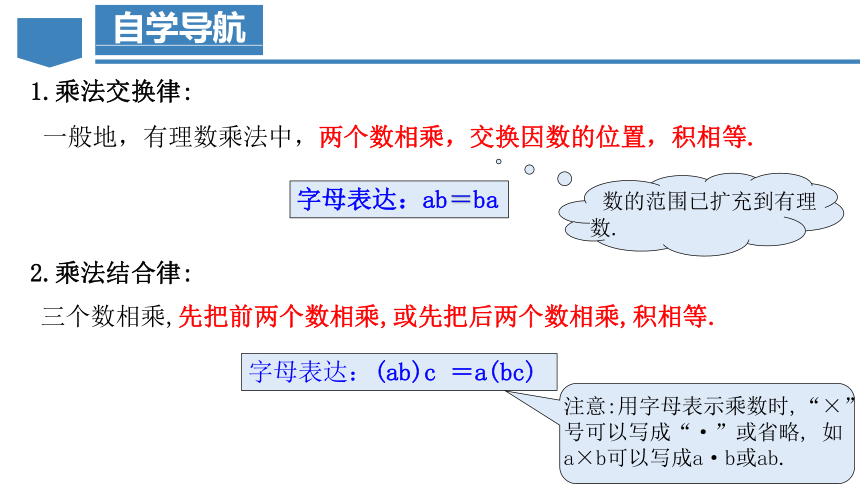
一般地,有理数乘法中,两个数相乘,交换因数的位置,积相等.
字母表达:ab=ba
三个数相乘,先把前两个数相乘,或先把后两个数相乘,积相等.
字母表达:(ab)c =a(bc)
1.乘法交换律:
2.乘法结合律:
数的范围已扩充到有理数.
注意:用字母表示乘数时,“×”号可以写成“·”或省略, 如a×b可以写成a·b或ab.
解:(1)原式=-(4×)×(×)=-1;
(2)原式=(24×)×(96×)
=18×2
=36.
例1.计算:
(1)(-4)××(-0.25)×(-); (2)24×(-96)×0.75×(-).
分析:根据算式中数的特征以及运算律的作用,选择合适的乘法运算律简化计算.
有理数乘法运算律
重点
倒数结合
_____
_____
凑整结合
______
______
1.在(-0.125)×(-2)×(-8)×5=[(-0.125)×(-8)]×[(-2)×5]中,运用了( )
A.分配律 B.乘法交换律
C.乘法结合律 D.乘法交换律和乘法结合律
D
2.计算:
(1)(-4)×(-23)×(-25); (2)1.5×0.5×(-100)×;
(3)(-3)×(-)×(-)×(-).
解:(1)原式=-(4×25×23)=-2300;
(2)原式=-(×)×(0.5×)=-1×50=-50;
(3)原式=(3×)×()=1×4=4.
5×[3+(-7)]=___________=_____,5×3+5×(-7)=__________=_____;
即
[2+(-4)]×(-3)=__________=___,2×(-3)+(-4)×(-3)=________=___.
即
5×(-4)
-20
15+(-35)
-20
5×[3+(-7)]=5×3+5×(-7);
(-2)×(-3)
6
(-6)+12
6
[2+(-4)]×(-3)=2×(-3)+(-4)×(-3).
上面每组运算体现了什么运算律?
一般地,有理数乘法中,一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
字母表达:a(b+c)= ab+ac
3.乘法分配律:
有理数乘法运算律
重点
例2.利用乘法的运算律进行计算:
(-+-)×(-36)
解:原式=(-)×(-36)+×(-36)-×(-36)
=3-9-(-30)
=24.
1.计算(-+-)×24的结果是( )
A.-2 B.-3 C.-4 D.-5
2.利用乘法的运算律进行计算:-×(8-1-0.04).
D
解:原式=-×8-()×-()×0.04
=-6-(-1)-(-0.03)
=-6+1+0.03
=-4.97.
有理数加减和乘法混合运算
重点
例3.计算:
(1)(-4)×(-8)×(-)-(-6)+6×; (2)-3-4×(-)-3×.
解:(1)原式=-32×+6+4
=-6+6+4
=4;
(2)原式=-3-(-6)-1
=-3+6-1
=2.
例4.计算:
-5×3+2×3+(-6)×3.
解:原式=[-5+2+(-6)]×3
=-9×
=-30.
逆用分配律进行简便运算
难点
计算:
(1)99×18+99×(-)-99×8; (2)-13×-0.34×+×(-13)-×0.34.
解:(1)原式=99×(18--8)
=99×10
=990;
(2)原式=(+)×(-13)+(+)×(-0.34)
=-13+(-0.34)
=-13.34.
巧用拆分法与分配律进行简便运算
难点
例5.计算:(-99)×32.
解法1:
解:原式=[(-99)+(-)]×32
=-3168+(-30)
=-3198.
解法2:
解:原式=[(-100)+]×32
=-3200+2
=-3198.
计算:
(1)999×(-15); (2)(-125)×(-); (3)49×(-5).
解:(1)原式=(1000-1)×(-15)
=-15000+15
=-14985;
(2)原式=(125+)×
=25+
=25;
(3)原式=-(50-)×5
=-(250-)
=-24.
利用裂项法进行简便运算
难点
例6.计算:+++…+.
利用裂项法进行简便运算
难点
例6.计算:+++…+.
解:原式=×(1-)+×(-)+×(-)+…+×(-)
=×(1-+-+-+…+-)
=×(1-)
=×
=
计算:+++…+.
解:原式=×(1-)+×(-)+×(-)+…+×(-)
=×(1-+-+-+…+-)
=×(1-)
=×
=
有理数加减和乘法混合运算的实际应用
重难点
例7.有30筐白菜,以每筐25kg为标准,超过或不足的千克数分别用正、负数表示:
求这30筐白菜的总质量.
有理数加减和乘法混合运算的实际应用
重难点
解:25×30+4×(-0.8)+6×(+0.6)+3×(-0.5)+4×(+0.4)+4×(+0.5)+4×(-0.3)+5×(+0.3)
=750+(-3.2)+3.6+(-1.5)+1.6+2+(-1.2)+1.5
=752.8(kg).
答:这30筐白菜的总质量是752.8kg.
某服装店以每件35元的价格购进了30件连衣裙,针对不同的顾客,30件连衣裙的售价不完全相同.若以50元为标准售价,将超过的钱数记为正数,不足的钱数记为负数,记录结果如下:
该服装店售完这30件连衣裙后,赚了多少钱
解:(50-35)×30+7×(+3)+6×(+2)+3×(+1)+5×0+4×(-1)+5×(-2)
=450+21+12+3+0-4-10
=472(元).
答:该服装店售完这30件连衣裙后,赚了472元钱.
一般地,有理数乘法中,两个数相乘,交换因数的位置,积相等.
字母表达:ab=ba
三个数相乘,先把前两个数相乘,或先把后两个数相乘,积相等.
字母表达:(ab)c =a(bc)
1.乘法交换律:
2.乘法结合律:
一般地,有理数乘法中,一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
字母表达:a(b+c)= ab+ac
3.乘法分配律:
第1章 有理数
1.4.1 有理数的乘法
第一单元
1.掌握有理数乘法的运算律,并利用运算律简化乘法运算. (运算能力)
2掌握乘法的分配律,并能灵活的运用. (运算能力)
一、有理数乘法法则
1.两数相乘,同号得正,异号得负,并把绝对值相乘.
2.任何数同0相乘,都得0.
思考:(1)若a<0,b>0,则ab 0 ;
(2)若a<0,b<0,则ab 0 ;
(3)若ab>0,则a、b应满足什么条件?
(4)若ab<0,则a、b应满足什么条件?
<
>
a、b同号
a、b异号
1.几个非零的数相乘:
几个不是0的数相乘,当负因数的个数是_____时,积是正数;当负因数的个数是_____时,积是负数.
偶数
奇数
二、多个有理数相乘的运算规律
2.几个数相乘,其中含有0:
几个数相乘,如果其中有因数为0,那么积等于0.
4×(-5)=____,(-5)×4=____; 6×(-2)=____,(-2)×6=____;
即
[2×(-3)]×(-5)=__________=____,2×[(-3)×(-5)]=_______=____.
即
-20
-20
4×(-5)=(-5)×4;
6×(-2)=(-2)×6.
-12
-12
(-6)×(-5)
30
2×15
30
[2×(-3)]×(-5)=2×[(-3)×(-5)]
上面每组运算分别体现了什么运算律?
一般地,有理数乘法中,两个数相乘,交换因数的位置,积相等.
字母表达:ab=ba
三个数相乘,先把前两个数相乘,或先把后两个数相乘,积相等.
字母表达:(ab)c =a(bc)
1.乘法交换律:
2.乘法结合律:
数的范围已扩充到有理数.
注意:用字母表示乘数时,“×”号可以写成“·”或省略, 如a×b可以写成a·b或ab.
解:(1)原式=-(4×)×(×)=-1;
(2)原式=(24×)×(96×)
=18×2
=36.
例1.计算:
(1)(-4)××(-0.25)×(-); (2)24×(-96)×0.75×(-).
分析:根据算式中数的特征以及运算律的作用,选择合适的乘法运算律简化计算.
有理数乘法运算律
重点
倒数结合
_____
_____
凑整结合
______
______
1.在(-0.125)×(-2)×(-8)×5=[(-0.125)×(-8)]×[(-2)×5]中,运用了( )
A.分配律 B.乘法交换律
C.乘法结合律 D.乘法交换律和乘法结合律
D
2.计算:
(1)(-4)×(-23)×(-25); (2)1.5×0.5×(-100)×;
(3)(-3)×(-)×(-)×(-).
解:(1)原式=-(4×25×23)=-2300;
(2)原式=-(×)×(0.5×)=-1×50=-50;
(3)原式=(3×)×()=1×4=4.
5×[3+(-7)]=___________=_____,5×3+5×(-7)=__________=_____;
即
[2+(-4)]×(-3)=__________=___,2×(-3)+(-4)×(-3)=________=___.
即
5×(-4)
-20
15+(-35)
-20
5×[3+(-7)]=5×3+5×(-7);
(-2)×(-3)
6
(-6)+12
6
[2+(-4)]×(-3)=2×(-3)+(-4)×(-3).
上面每组运算体现了什么运算律?
一般地,有理数乘法中,一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
字母表达:a(b+c)= ab+ac
3.乘法分配律:
有理数乘法运算律
重点
例2.利用乘法的运算律进行计算:
(-+-)×(-36)
解:原式=(-)×(-36)+×(-36)-×(-36)
=3-9-(-30)
=24.
1.计算(-+-)×24的结果是( )
A.-2 B.-3 C.-4 D.-5
2.利用乘法的运算律进行计算:-×(8-1-0.04).
D
解:原式=-×8-()×-()×0.04
=-6-(-1)-(-0.03)
=-6+1+0.03
=-4.97.
有理数加减和乘法混合运算
重点
例3.计算:
(1)(-4)×(-8)×(-)-(-6)+6×; (2)-3-4×(-)-3×.
解:(1)原式=-32×+6+4
=-6+6+4
=4;
(2)原式=-3-(-6)-1
=-3+6-1
=2.
例4.计算:
-5×3+2×3+(-6)×3.
解:原式=[-5+2+(-6)]×3
=-9×
=-30.
逆用分配律进行简便运算
难点
计算:
(1)99×18+99×(-)-99×8; (2)-13×-0.34×+×(-13)-×0.34.
解:(1)原式=99×(18--8)
=99×10
=990;
(2)原式=(+)×(-13)+(+)×(-0.34)
=-13+(-0.34)
=-13.34.
巧用拆分法与分配律进行简便运算
难点
例5.计算:(-99)×32.
解法1:
解:原式=[(-99)+(-)]×32
=-3168+(-30)
=-3198.
解法2:
解:原式=[(-100)+]×32
=-3200+2
=-3198.
计算:
(1)999×(-15); (2)(-125)×(-); (3)49×(-5).
解:(1)原式=(1000-1)×(-15)
=-15000+15
=-14985;
(2)原式=(125+)×
=25+
=25;
(3)原式=-(50-)×5
=-(250-)
=-24.
利用裂项法进行简便运算
难点
例6.计算:+++…+.
利用裂项法进行简便运算
难点
例6.计算:+++…+.
解:原式=×(1-)+×(-)+×(-)+…+×(-)
=×(1-+-+-+…+-)
=×(1-)
=×
=
计算:+++…+.
解:原式=×(1-)+×(-)+×(-)+…+×(-)
=×(1-+-+-+…+-)
=×(1-)
=×
=
有理数加减和乘法混合运算的实际应用
重难点
例7.有30筐白菜,以每筐25kg为标准,超过或不足的千克数分别用正、负数表示:
求这30筐白菜的总质量.
有理数加减和乘法混合运算的实际应用
重难点
解:25×30+4×(-0.8)+6×(+0.6)+3×(-0.5)+4×(+0.4)+4×(+0.5)+4×(-0.3)+5×(+0.3)
=750+(-3.2)+3.6+(-1.5)+1.6+2+(-1.2)+1.5
=752.8(kg).
答:这30筐白菜的总质量是752.8kg.
某服装店以每件35元的价格购进了30件连衣裙,针对不同的顾客,30件连衣裙的售价不完全相同.若以50元为标准售价,将超过的钱数记为正数,不足的钱数记为负数,记录结果如下:
该服装店售完这30件连衣裙后,赚了多少钱
解:(50-35)×30+7×(+3)+6×(+2)+3×(+1)+5×0+4×(-1)+5×(-2)
=450+21+12+3+0-4-10
=472(元).
答:该服装店售完这30件连衣裙后,赚了472元钱.
一般地,有理数乘法中,两个数相乘,交换因数的位置,积相等.
字母表达:ab=ba
三个数相乘,先把前两个数相乘,或先把后两个数相乘,积相等.
字母表达:(ab)c =a(bc)
1.乘法交换律:
2.乘法结合律:
一般地,有理数乘法中,一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
字母表达:a(b+c)= ab+ac
3.乘法分配律:
