2.2.1 圆的对称性-圆心角、弧、弦的关系 课件(34张PPT)
文档属性
| 名称 | 2.2.1 圆的对称性-圆心角、弧、弦的关系 课件(34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 35.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 00:00:00 | ||
图片预览







文档简介
(共34张PPT)
2.2.1 圆的对称性
———圆心角、弧、弦的关系
第2章对称图形——圆
教学目标
01
认识圆的对称性,圆既是中心对称图形,也是轴对称图形
03
02
理解圆心角、弧、弦之间的关系,能快速地对三者之间关系的描述进行辨析
理解圆心角的度数与它所对弧的度数的等价关系
圆的对称性
01
复习引入Part1
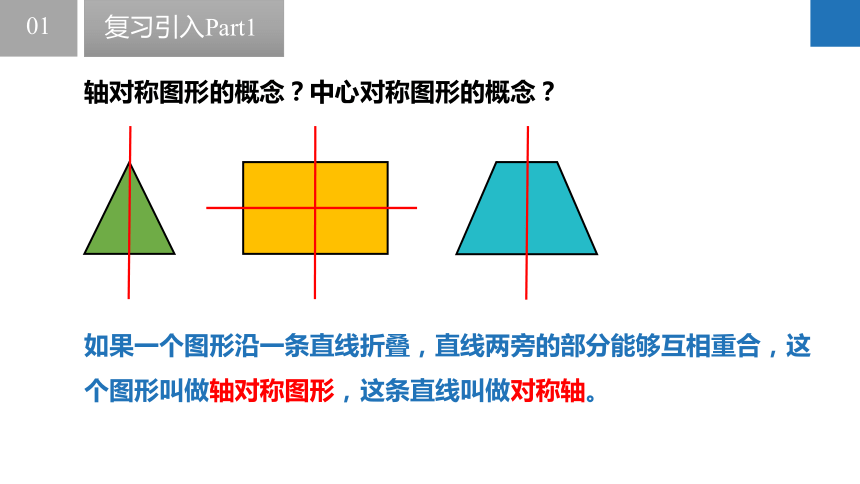
轴对称图形的概念?中心对称图形的概念?
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴。
01
复习引入Part1
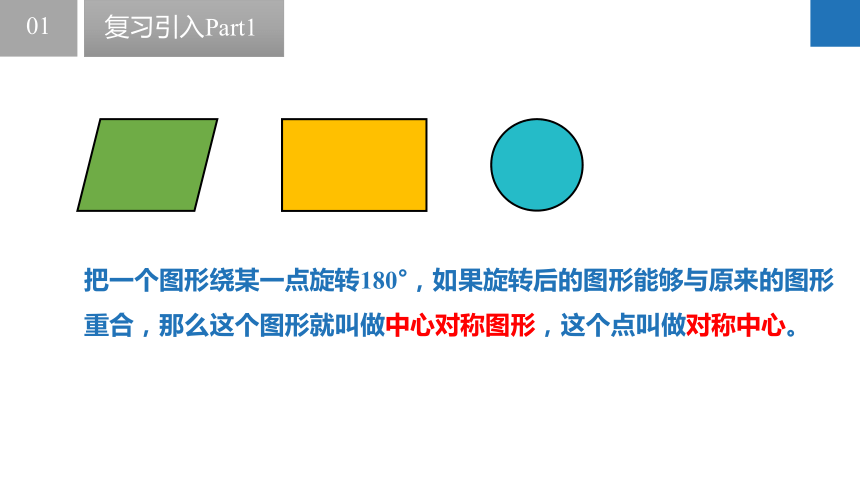
把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心。
上节课,我们从“一中同长”的角度解释了车轮为什么是圆的
圆形车轮正中心到车轮边上的距离处处相等,行驶起来更平稳,不容易颠簸.
01
复习引入Part2
从旋转的角度来看,轮子绕固定轴心旋转,不论转到什么位置,都与初始位置重合。
【总结】一个圆绕圆心旋转任何角度后,都能与原来的图形重合(旋转不变形)。
在纸上画O,把O剪下并折叠,使折痕两旁的部分完全重合,你发现了什么?
01
复习引入Part2
折痕过圆心O。
O
02
二、定义
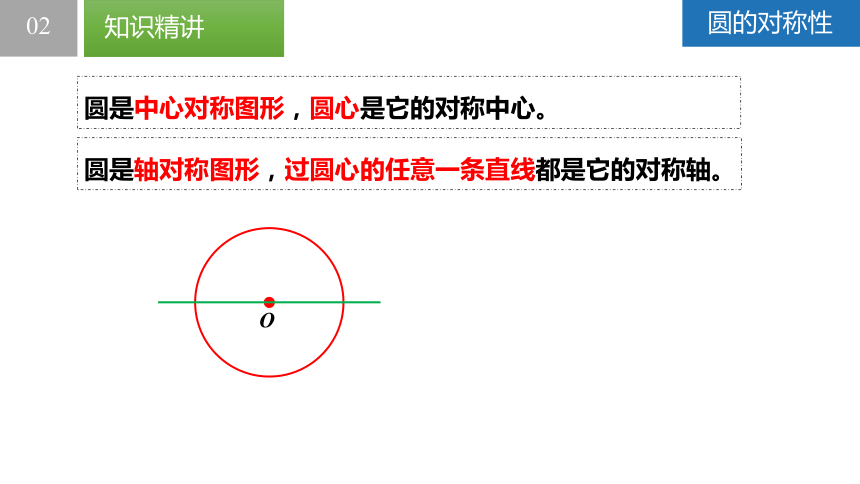
圆是中心对称图形,圆心是它的对称中心。
知识精讲
O
圆的对称性
圆是轴对称图形,过圆心的任意一条直线都是它的对称轴。
02
二、定义
小明老师有个问题想问大家
知识精讲
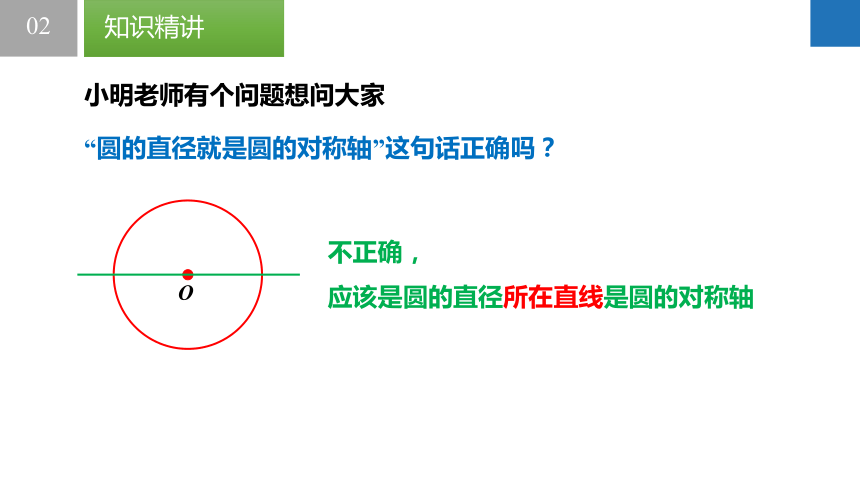
“圆的直径就是圆的对称轴”这句话正确吗?
O
不正确,
应该是圆的直径所在直线是圆的对称轴
例、判断正误:
(1)圆是中心对称图形,圆心就是对称中心;
(2)圆是轴对称图形,任意一条通过圆心的直线都是它的一条对称轴;
(3)圆是轴对称图形,其对称轴是任意一条直径.
03
典例精析
√
√
×,其对称轴是任意一条直径所在直线
圆心角、弧、弦的关系
02
二、定义
知识精讲
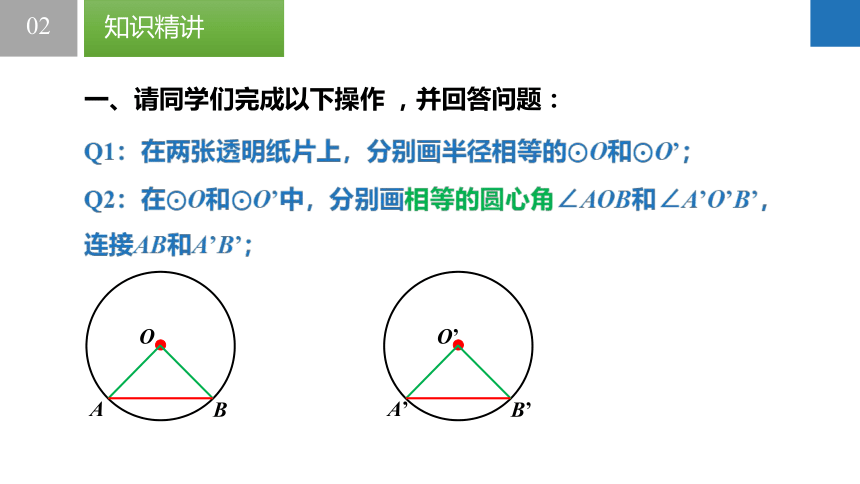
一、请同学们完成以下操作 ,并回答问题:
Q2:在O和O’中,分别画相等的圆心角∠AOB和∠A’O’B’,连接AB和A’B’;
Q1:在两张透明纸片上,分别画半径相等的O和O’;
O
O’
A
B
A’
B’
02
二、定义
知识精讲
Q3:在所画图中还有哪些相等的线段、相等的弧?
O
A
B
通过平移可知:AB=A’B’,
【总结】在等圆中,相等的圆心角所对的弧相等,所对的弦相等。
O’
A’
B’
02
二、定义
知识精讲
O
A
B
通过旋转可知:AB=A’’B’’,
Q4:将圆O中的圆心角∠AOB绕点O旋转,旋转后的圆心角记作∠A’’OB’’,连接A’’B’’,你发现了什么?
【总结】在同圆中,相等的圆心角所对的弧相等,所对的弦相等。
A’’
B’’
A’
B’
A’’
B’’
A’
B’
02
二、定义
知识精讲
圆心角、弧、弦的关系
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等。
O
A
B
A’’
B’’
O’
A’
B’
02
二、定义
知识精讲
圆心角、弧、弦的关系
小明老师有个问题想问大家
Q:“相等的圆心角所对的弧相等,所对的弦相等”这句话正确吗?
O
A
B
A’
B’
不正确,
必须强调“在同圆或者等圆中”这个前提条件
02
二、定义
知识精讲
二、在同圆或等圆中,如果圆心角所对的弧相等,那么它们所对的弦相等吗?这两个圆心角相等吗?
相等;相等。
O
A
B
A’’
B’’
O’
A’
B’
02
二、定义
知识精讲
圆心角、弧、弦的关系
在同圆或等圆中,相等的弧所对的弦相等,所对的圆心角相等。
O
A
B
A’’
B’’
O’
A’
B’
02
二、定义
知识精讲
圆心角、弧、弦的关系
小明老师有个问题想问大家
Q:“相等的弧,所对的弦相等,所对的圆心角相等”这句话正确吗?
正确,
相等的弧(等弧)一定是同圆或等圆中的弧,不缺少前提条件
相等的弧(等弧):
(1)能够互相重合的弧;
(2)在同圆或等圆中,长度相等的弧。
02
二、定义
知识精讲
圆心角、弧、弦的关系
三、在同圆或等圆中,如果圆心角所对的弦相等,那么它们所对的弧相等吗?这两个圆心角相等吗?
优弧与优弧相等,劣弧与劣弧相等;相等。
O
A
B
A’’
B’’
O’
A’
B’
02
二、定义
知识精讲
圆心角、弧、弦的关系
在同圆或等圆中,相等的弦所对的弧(优弧与优弧、劣弧与劣弧)相等,所对的圆心角相等。
O
A
B
A’’
B’’
O’
A’
B’
02
二、定义
知识精讲
圆心角、弧、弦的关系
小明老师有个问题想问大家
“在同圆或等圆中,相等的弦所对弧相等”这句话正确吗?
不正确,
应是“在同圆或等圆中,相等的弦所对的优弧和劣弧分别相等”。
O
A
B
O’
A’
B’
02
二、定义
知识精讲
圆心角、弧、弦的关系
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
注意:
(1)“在同圆或等圆中”这个前提条件很重要;
(2)已知一组量为“两条弧相等”,就已经默认了“在同圆或等圆中”;
(3)“在同圆或等圆中”,已知一组量为“两条弦相等”,必须强调“所对的优弧和劣弧分别相等”。
例1、判断正误:
(1)相等的圆心角所对的弧相等;
(2)相等的弧所对的弦一定相等;
(3)在同圆或等圆中,相等的弦所对的弧也一定相等.
03
典例精析
×,在同圆或等圆中
√,相等的弧(等弧)已经默认“在同圆或等圆中”这个前提条件
×,在同圆或等圆中,相等的弦所对的优弧和劣弧分别相等
例2、(1)若一条弦把圆周分成2:3的两段弧,则劣弧所对圆心角的度数是________°.
03
典例精析
解:∵一条弦把圆周分成2:3的两段弧,
∴劣弧所对圆心角的度数为360°×=144°.
144
例2、(2)如图,AB是O的直径,==,∠COD=34°,则∠AEO的度数是________°.
03
典例精析
解:如图,∵==,∠COD=34°,
∴∠BOC=∠EOD=∠COD=34°,
∴∠AOE=180°-∠EOD-∠COD-∠BOC=78°,
又∵OA=OE,∴∠AEO=∠OAE,
∴∠AEO=×(180°-78°)=51°.
51
例3、(1)如图,已知在O中,BC是直径,AB=DC,则下列结论不一定成立的是( )
A.OA=OB=AB B.∠AOB=∠COD
C.= D.O到AB、CD的距离相等
03
典例精析
解∵AB=DC,∴=,∠AOB=∠COD,
∵OA=OB=OC=OD,∴△AOB≌△COD(SAS),
∴O到AB、CD的距离相等.
A
例3、(2)如图,AB是O的直径,四边形ABCD内接于O,若BC=CD=DA=4,则O的周长为( )
A.4π B.6π C.8π D.9π
03
典例精析
解:如图,连接OC、OD,
∵BC=CD=DA=4,
∴==,∠AOD=∠DOC=∠BOC=60°,
又∵OA=OD,∴△AOD是等边三角形,
∴OA=AD=4,∴O的周长=2×4π=8π.
C
例4、如图,在O中,=2,则下列结论正确的是( )
A.AB>2CD B.AB=2CD
C.AB<2CD D.以上都不正确
03
典例精析
解:如图,取的中点E,连接AE,BE,
∵在O中,=2,∴==,
∴AE=BE=CD,
∵AE+BE>AB,
∴2CD>AB.
C
E
圆心角的度数与它所对的弧的度数
02
二、定义
知识精讲
圆心角的度数与它所对的弧的度数
我们知道,将顶点在圆心的周角等分成360份,每一份圆心角是1°的角,因为同圆中相等的圆心角所对的弧相等,所以整个圆也被等分成360份。我们把1°的圆心角所对的弧叫做1°的弧。
O
1°的弧
1°的圆心角
02
二、定义
知识精讲
圆心角的度数与它所对的弧的度数
一般地,n°的圆心角对着n°的弧,n°的弧对着n°的圆心角。
O
1°的弧
1°的圆心角
A
B
n°的弧
n°的圆心角
例、若弦长等于半径,则弦所对弧的度数是__________.
03
典例精析
解:∵弦长等于半径,
∴由弦和经过弦的端点的两半径组成等边三角形,
∴弦所对的圆心角是60°,
∴弦多对的劣弧的度数是60°,弦所对的优弧的度数是300°.
60°或300°
课后总结
圆是中心对称图形,圆心是它的对称中心。
圆是轴对称图形,过圆心的任意一条直线都是它的对称轴。
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
注意:
(1)“在同圆或等圆中”这个前提条件很重要;
(2)已知一组量为“两条弧相等”,就已经默认了“在同圆或等圆中”;
(3)“在同圆或等圆中”,已知一组量为“两条弦相等”,必须强调“所对的优弧和劣弧分别相等”。
一般地,n°的圆心角对着n°的弧,n°的弧对着n°的圆心角。
2.2.1 圆的对称性
———圆心角、弧、弦的关系
第2章对称图形——圆
教学目标
01
认识圆的对称性,圆既是中心对称图形,也是轴对称图形
03
02
理解圆心角、弧、弦之间的关系,能快速地对三者之间关系的描述进行辨析
理解圆心角的度数与它所对弧的度数的等价关系
圆的对称性
01
复习引入Part1
轴对称图形的概念?中心对称图形的概念?
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴。
01
复习引入Part1
把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心。
上节课,我们从“一中同长”的角度解释了车轮为什么是圆的
圆形车轮正中心到车轮边上的距离处处相等,行驶起来更平稳,不容易颠簸.
01
复习引入Part2
从旋转的角度来看,轮子绕固定轴心旋转,不论转到什么位置,都与初始位置重合。
【总结】一个圆绕圆心旋转任何角度后,都能与原来的图形重合(旋转不变形)。
在纸上画O,把O剪下并折叠,使折痕两旁的部分完全重合,你发现了什么?
01
复习引入Part2
折痕过圆心O。
O
02
二、定义
圆是中心对称图形,圆心是它的对称中心。
知识精讲
O
圆的对称性
圆是轴对称图形,过圆心的任意一条直线都是它的对称轴。
02
二、定义
小明老师有个问题想问大家
知识精讲
“圆的直径就是圆的对称轴”这句话正确吗?
O
不正确,
应该是圆的直径所在直线是圆的对称轴
例、判断正误:
(1)圆是中心对称图形,圆心就是对称中心;
(2)圆是轴对称图形,任意一条通过圆心的直线都是它的一条对称轴;
(3)圆是轴对称图形,其对称轴是任意一条直径.
03
典例精析
√
√
×,其对称轴是任意一条直径所在直线
圆心角、弧、弦的关系
02
二、定义
知识精讲
一、请同学们完成以下操作 ,并回答问题:
Q2:在O和O’中,分别画相等的圆心角∠AOB和∠A’O’B’,连接AB和A’B’;
Q1:在两张透明纸片上,分别画半径相等的O和O’;
O
O’
A
B
A’
B’
02
二、定义
知识精讲
Q3:在所画图中还有哪些相等的线段、相等的弧?
O
A
B
通过平移可知:AB=A’B’,
【总结】在等圆中,相等的圆心角所对的弧相等,所对的弦相等。
O’
A’
B’
02
二、定义
知识精讲
O
A
B
通过旋转可知:AB=A’’B’’,
Q4:将圆O中的圆心角∠AOB绕点O旋转,旋转后的圆心角记作∠A’’OB’’,连接A’’B’’,你发现了什么?
【总结】在同圆中,相等的圆心角所对的弧相等,所对的弦相等。
A’’
B’’
A’
B’
A’’
B’’
A’
B’
02
二、定义
知识精讲
圆心角、弧、弦的关系
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等。
O
A
B
A’’
B’’
O’
A’
B’
02
二、定义
知识精讲
圆心角、弧、弦的关系
小明老师有个问题想问大家
Q:“相等的圆心角所对的弧相等,所对的弦相等”这句话正确吗?
O
A
B
A’
B’
不正确,
必须强调“在同圆或者等圆中”这个前提条件
02
二、定义
知识精讲
二、在同圆或等圆中,如果圆心角所对的弧相等,那么它们所对的弦相等吗?这两个圆心角相等吗?
相等;相等。
O
A
B
A’’
B’’
O’
A’
B’
02
二、定义
知识精讲
圆心角、弧、弦的关系
在同圆或等圆中,相等的弧所对的弦相等,所对的圆心角相等。
O
A
B
A’’
B’’
O’
A’
B’
02
二、定义
知识精讲
圆心角、弧、弦的关系
小明老师有个问题想问大家
Q:“相等的弧,所对的弦相等,所对的圆心角相等”这句话正确吗?
正确,
相等的弧(等弧)一定是同圆或等圆中的弧,不缺少前提条件
相等的弧(等弧):
(1)能够互相重合的弧;
(2)在同圆或等圆中,长度相等的弧。
02
二、定义
知识精讲
圆心角、弧、弦的关系
三、在同圆或等圆中,如果圆心角所对的弦相等,那么它们所对的弧相等吗?这两个圆心角相等吗?
优弧与优弧相等,劣弧与劣弧相等;相等。
O
A
B
A’’
B’’
O’
A’
B’
02
二、定义
知识精讲
圆心角、弧、弦的关系
在同圆或等圆中,相等的弦所对的弧(优弧与优弧、劣弧与劣弧)相等,所对的圆心角相等。
O
A
B
A’’
B’’
O’
A’
B’
02
二、定义
知识精讲
圆心角、弧、弦的关系
小明老师有个问题想问大家
“在同圆或等圆中,相等的弦所对弧相等”这句话正确吗?
不正确,
应是“在同圆或等圆中,相等的弦所对的优弧和劣弧分别相等”。
O
A
B
O’
A’
B’
02
二、定义
知识精讲
圆心角、弧、弦的关系
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
注意:
(1)“在同圆或等圆中”这个前提条件很重要;
(2)已知一组量为“两条弧相等”,就已经默认了“在同圆或等圆中”;
(3)“在同圆或等圆中”,已知一组量为“两条弦相等”,必须强调“所对的优弧和劣弧分别相等”。
例1、判断正误:
(1)相等的圆心角所对的弧相等;
(2)相等的弧所对的弦一定相等;
(3)在同圆或等圆中,相等的弦所对的弧也一定相等.
03
典例精析
×,在同圆或等圆中
√,相等的弧(等弧)已经默认“在同圆或等圆中”这个前提条件
×,在同圆或等圆中,相等的弦所对的优弧和劣弧分别相等
例2、(1)若一条弦把圆周分成2:3的两段弧,则劣弧所对圆心角的度数是________°.
03
典例精析
解:∵一条弦把圆周分成2:3的两段弧,
∴劣弧所对圆心角的度数为360°×=144°.
144
例2、(2)如图,AB是O的直径,==,∠COD=34°,则∠AEO的度数是________°.
03
典例精析
解:如图,∵==,∠COD=34°,
∴∠BOC=∠EOD=∠COD=34°,
∴∠AOE=180°-∠EOD-∠COD-∠BOC=78°,
又∵OA=OE,∴∠AEO=∠OAE,
∴∠AEO=×(180°-78°)=51°.
51
例3、(1)如图,已知在O中,BC是直径,AB=DC,则下列结论不一定成立的是( )
A.OA=OB=AB B.∠AOB=∠COD
C.= D.O到AB、CD的距离相等
03
典例精析
解∵AB=DC,∴=,∠AOB=∠COD,
∵OA=OB=OC=OD,∴△AOB≌△COD(SAS),
∴O到AB、CD的距离相等.
A
例3、(2)如图,AB是O的直径,四边形ABCD内接于O,若BC=CD=DA=4,则O的周长为( )
A.4π B.6π C.8π D.9π
03
典例精析
解:如图,连接OC、OD,
∵BC=CD=DA=4,
∴==,∠AOD=∠DOC=∠BOC=60°,
又∵OA=OD,∴△AOD是等边三角形,
∴OA=AD=4,∴O的周长=2×4π=8π.
C
例4、如图,在O中,=2,则下列结论正确的是( )
A.AB>2CD B.AB=2CD
C.AB<2CD D.以上都不正确
03
典例精析
解:如图,取的中点E,连接AE,BE,
∵在O中,=2,∴==,
∴AE=BE=CD,
∵AE+BE>AB,
∴2CD>AB.
C
E
圆心角的度数与它所对的弧的度数
02
二、定义
知识精讲
圆心角的度数与它所对的弧的度数
我们知道,将顶点在圆心的周角等分成360份,每一份圆心角是1°的角,因为同圆中相等的圆心角所对的弧相等,所以整个圆也被等分成360份。我们把1°的圆心角所对的弧叫做1°的弧。
O
1°的弧
1°的圆心角
02
二、定义
知识精讲
圆心角的度数与它所对的弧的度数
一般地,n°的圆心角对着n°的弧,n°的弧对着n°的圆心角。
O
1°的弧
1°的圆心角
A
B
n°的弧
n°的圆心角
例、若弦长等于半径,则弦所对弧的度数是__________.
03
典例精析
解:∵弦长等于半径,
∴由弦和经过弦的端点的两半径组成等边三角形,
∴弦所对的圆心角是60°,
∴弦多对的劣弧的度数是60°,弦所对的优弧的度数是300°.
60°或300°
课后总结
圆是中心对称图形,圆心是它的对称中心。
圆是轴对称图形,过圆心的任意一条直线都是它的对称轴。
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
注意:
(1)“在同圆或等圆中”这个前提条件很重要;
(2)已知一组量为“两条弧相等”,就已经默认了“在同圆或等圆中”;
(3)“在同圆或等圆中”,已知一组量为“两条弦相等”,必须强调“所对的优弧和劣弧分别相等”。
一般地,n°的圆心角对着n°的弧,n°的弧对着n°的圆心角。
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
