2.2.2 圆的对称性-垂径定理 课件(31张PPT)
文档属性
| 名称 | 2.2.2 圆的对称性-垂径定理 课件(31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 35.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 09:46:49 | ||
图片预览









文档简介
2.2.2 圆的对称性
——垂径定理
第2章对称图形——圆
教学目标
01
掌握圆的垂径定理的证明与运用
02
掌握圆的垂径定理的三个推论的证明与运用
垂径定理
01
二、定义
情境引入
请同学们完成以下操作 ,并回答问题:
Q1:画?O和?O的直径AB、弦CD,使AB⊥CD,垂足为P;
?
O
C
D
A
B
P
二、定义
Q2:在所画图中有哪些相等的线段、相等的弧?
O
C
A
B
P
D
(D)
由翻折可知:PC=PD,????????=????????,????????=????????。
?
01
二、定义
情境引入
Q3:是否还有其他的方法证明:PC=PD,????????=????????,????????=?????????
?
已知:AB是?O的直径,CD是?O的弦,AB⊥CD,垂直为P。
?
O
C
D
A
B
P
解:如图,连接OC、OD,
在Rt△OCP和Rt△ODP中,
????????=????????????????=????????,
∴△OPC?△OPD(HL),
?
∴PC=PD,∠BOC=∠BOD,
∴????????=????????,∠AOC=∠AOD,
∴????????=????????。
?
01
二、定义
情境引入
02
二、定义
知识精讲
垂径定理
垂直于弦的直径平分弦以及弦所对的两条弧。
O
C
D
A
B
P
符号语言(知二推三):
AB过圆心(AB为?O的直径),AB⊥CD
?PC=PD,????????=????????,????????=????????。
?
02
二、定义
知识精讲
弦心距
在一个圆中,圆心到弦的垂线段的长度(或圆心到弦的距离),叫做弦心距。
O
C
D
P
eg:OP的长度
02
二、定义
知识精讲
小明老师有几个问题想问大家
解:设?O的半径为r,
∵CD是?O的弦,OP⊥CD于点P,
∴CP=DP=????????CD(垂径定理),
在Rt△OPC中,OC2=OP2+CP2,
∴r2=OP2+????????CD2。
?
O
C
D
P
Q1:已知:OC是?O的半径,CD是?O的弦,OP⊥CD于点P,问:OC、OP、CD之间的数量关系?
?
02
二、定义
知识精讲
O
C
D
P
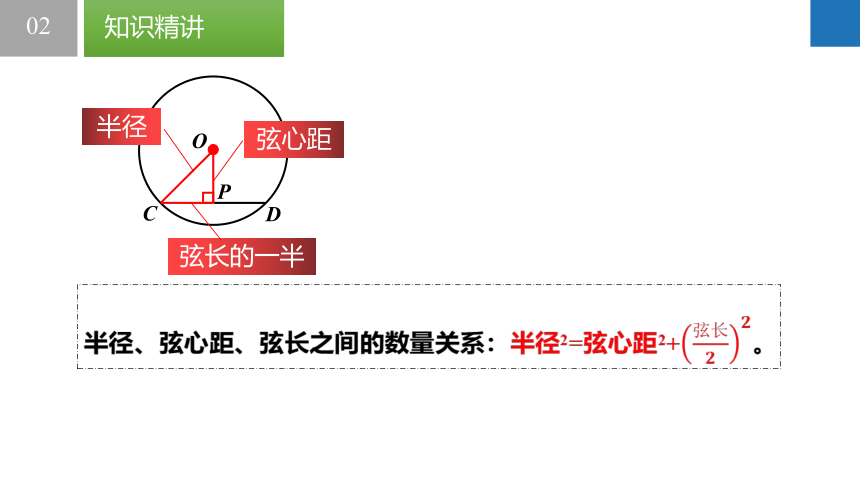
半径
弦心距
弦长的一半
半径、弦心距、弦长之间的数量关系:半径2=弦心距2+弦长????????。
?
02
二、定义
知识精讲
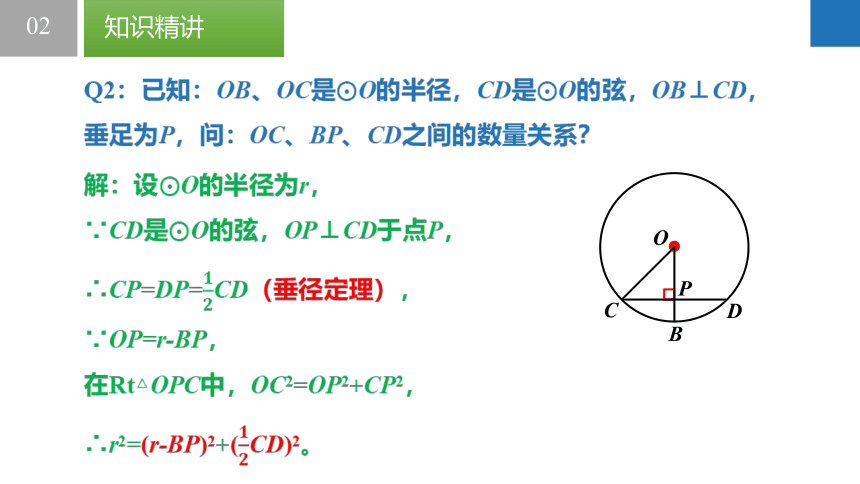
解:设?O的半径为r,
∵CD是?O的弦,OP⊥CD于点P,
∴CP=DP=????????CD(垂径定理),
∵OP=r-BP,
在Rt△OPC中,OC2=OP2+CP2,
∴r2=(r-BP)2+(????????CD)2。
?
Q2:已知:OB、OC是?O的半径,CD是?O的弦,OB⊥CD,垂足为P,问:OC、BP、CD之间的数量关系?
?
O
C
D
P
B
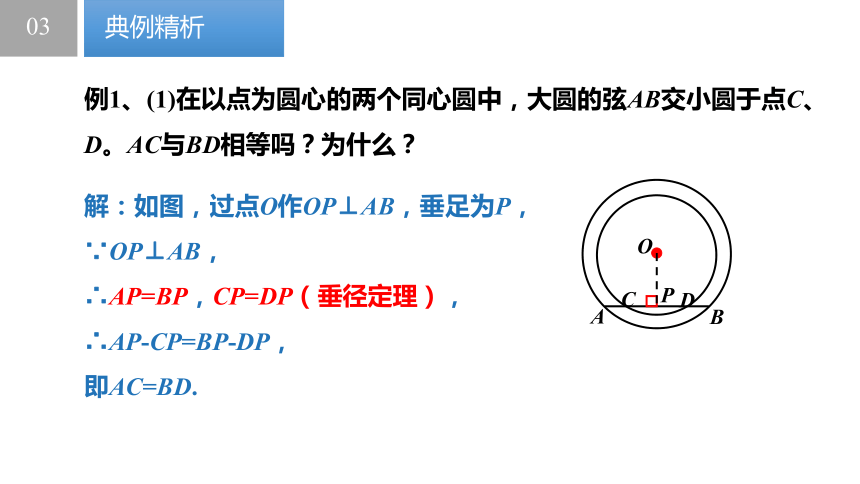
例1、(1)在以点为圆心的两个同心圆中,大圆的弦AB交小圆于点C、D。AC与BD相等吗?为什么?
03
典例精析
O
B
D
A
C
解:如图,过点O作OP⊥AB,垂足为P,
∵OP⊥AB,
∴AP=BP,CP=DP(垂径定理),
∴AP-CP=BP-DP,
即AC=BD.
P
例1、(2)AB、CD是?O的两条弦,AB∥CD。????????与????????相等吗?为什么?
?
03
典例精析
O
D
B
C
A
解:如图,作OQ⊥AB交?O于点Q,
∵OQ⊥AB,∴????????=????????(垂径定理),
又∵AB∥CD,
∴OQ⊥CD,∴????????=????????(垂径定理),
∴????????-????????=????????-????????,即????????=????????.
?
Q
例2、如图,点C是?O的弦AB上一点.若AC=6,BC=2,AB的弦心距为3,则OC的长为_________.
?
03
典例精析
解:如图,作OD⊥AB,垂足为D,
由题意可知:OD=3,
∵OD⊥AB,
∴BD=????????AB=????????(AC+BC)=4(垂径定理),
∴CD=BD-BC=2,
在Rt△OCD中,OC2=CD2+OD2=22+32=13,
∴OC=????????.
?
????????
?
D
例3、如图,AB是?O的直径,弦CD⊥AB于点E,若CD=6,AB=10,则AE的长为( )
A.1 B.2 C.3 D.4
?
03
典例精析
解:如图,连接OC,
在Rt△OCE中,OC2=CE2+OE2,
∵AB是?O的直径,AB=10,∴OC=5,
∵CD⊥AB ,∴CE=????????CD=3(垂径定理),
∴52=32+OE2,解得:OE=4,
∴AE=OA-OE=5-4=1.
?
A
例4、(1)如图,?O的直径AB垂直弦CD于点P,且P为半径OB的中点,若CD=6,则?O的半径长为_________.
?
03
典例精析
解:如图,连接OD,设?O的半径为r,
在Rt△ODP中,OD2=OP2+DP2,
∵P为半径OB的中点,∴OP=????????r,
∵?O的直径AB垂直弦CD于点P ,
∴DP=????????CD=3(垂径定理),
∴r2=(????????r)2+32,解得:r=2????.
?
2????
?
例4、(2)如图,AB是?O的直径,弦CD⊥AB 于E,若CD=4????,BE=2,则AB的长是_________.
?
03
典例精析
解:如图,连接OC,设?O的半径为r,
在Rt△OEC中,OC2=OE2+CE2,
∵BE=2,∴OE=r-2,
∵AB是?O的直径,CD⊥AB ,
∴CE=????????CD=2????(垂径定理),
∴r2=(r-2)2+(2????)2,解得:r=6,∴AB=2r=12.
?
12
垂径定理的推论
一、若已知:AB是?O的直径,CD是?O的弦,AB平分CD交CD于点P,能否推出:AB⊥CD,????????=????????,????????=?????????
?
02
二、定义
知识精讲
解:如图,连接OC、OD,
在△OPC和△OPD中,
????????=????????????????=????????????????=????????,
∴△OPC?△OPD(SSS),
?
O
C
D
A
B
P
∴∠APC=∠APD,
即AB⊥CD,
根据垂径定理:
∴????????=????????,????????=????????。
?
02
二、定义
知识精讲
垂径定理的推论1
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
O
C
D
A
B
P
符号语言(知二推三):
AB过圆心(AB为?O的直径),PC=PD
?AB⊥CD,????????=????????,????????=????????。
?
02
二、定义
知识精讲
垂径定理的推论1
注意:若此处的弦CD是直径,则结论不一定成立。
O
C
D
A
B
P
O
C
D
A
B
P
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
二、若已知:AB、CD是?O的弦,AB垂直平分CD交CD于点P,能否推出:AB过圆心,????????=????????,????????=?????????
?
02
二、定义
知识精讲
解:如图,连接OC、OD,
∵OC=OD,
∴O在CD的垂直平分线上,
即O在AB上,
∴AB过圆心(AB为?O的直径),
?
O
C
D
A
B
P
根据垂径定理或推论1:
∴????????=????????,????????=????????。
?
02
二、定义
知识精讲
垂径定理的推论2
弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
O
C
D
A
B
P
符号语言(知二推三):
AB⊥CD,PC=PD
?AB过圆心(AB为?O的直径),????????=????????,????????=????????。
?
三、(1)若已知:AB是?O的直径,????????=????????,连接CD交于AB点P,能否推出:AB⊥CD,PC=PD,????????=?????????
?
02
二、定义
知识精讲
解:如图,连接OC、OD、BC、BD,
∵AB是?O的直径,????????=????????,
∴BC=BD,????????-????????=????????-????????,即????????=????????,
又∵OC=OD,
∴AB垂直平分CD,
∴AB⊥CD,PC=PD。
?
O
C
D
A
B
P
三、(2)若已知:AB是?O的直径,????????=????????,连接CD交于AB点P,能否推出:AB⊥CD,PC=PD,????????=?????????
?
02
二、定义
知识精讲
解:连接OC、OD、BC、BD,
∵AB是?O的直径,????????=????????,
∴????????-????????=????????-????????,即????????=????????,
∴BC=BD,
?
O
C
D
A
B
P
又∵OC=OD,
∴AB垂直平分CD,
∴AB⊥CD,PC=PD。
02
二、定义
知识精讲
圆心角、弧、弦的关系
垂径定理的推论3
平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧。
符号语言(知二推三):
(1)AB过圆心(AB为?O的直径),????????=????????,
?AB⊥CD,PC=PD,????????=????????;
(2)AB过圆心(AB为?O的直径),????????=????????,
?AB⊥CD,PC=PD,????????=????????。
?
O
C
D
A
B
P
02
二、定义
知识精讲
圆心角、弧、弦的关系
垂径定理及其推论
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}①AB过圆心(AB为O的直径),②AB⊥CD,③PC=PD,④=,⑤=(知二推三)
文字语言
符号语言
垂径定理
垂直于弦的直径平分弦以及弦所对的两条弧
①②?③④⑤
推论1
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧
①③?②④⑤
推论2
弦的垂直平分线经过圆心,并且平分弦所对的两条弧
②③?①④⑤
推论3
平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧
①④?②③⑤
或①⑤?②③④
O
C
D
A
B
P
例1、如图,OA,OB,OC都是?O的半径,AC,OB交于点D.若AD=CD=8,OD=6,则BD的长为( )
A.5 B.4 C.3 D.2
?
03
典例精析
解:∵OB是?O的半径,AD=CD=8,
∴OB⊥AC(推论1),
在Rt△AOD中,OA2=AD2+OD2=82+62=100,
∴OA=10,∴OB=10,
∴BD=10-6=4.
?
B
例2、(1)如图,M是CD的中点,EM⊥CD,若CD=4,EM=6,则弧CED所在圆的半径为_________.
03
典例精析
解:设弧CED所在圆的半径为r,
∵M是CD的中点,EM⊥CD,
∴EM过圆心O,CM=????????CD=2(推论2),
如图,连接OC,
∵EM=6,∴OM=6-r,
在Rt△OCM中,OC2=CM2+OM2,即r2=22+(6-r)2,解得:r=????????????.
?
????????????
?
例2、(2)如图,在平面直角坐标系中,过格点A,B,C作一圆弧,则该弧的圆心的坐标为_________.
03
典例精析
解:如图,分别作弦AB、AC的垂直平分线,
设两条垂直平分线的交点为D,
根据垂径定理的推论2,点D即所求,坐标为:(2,0).
(2,0)
D
课后总结
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}①AB过圆心(AB为O的直径),②AB⊥CD,③PC=PD,④=,⑤=(知二推三)
文字语言
符号语言
垂径定理
垂直于弦的直径平分弦以及弦所对的两条弧
①②?③④⑤
推论1
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧
①③?②④⑤
推论2
弦的垂直平分线经过圆心,并且平分弦所对的两条弧
②③?①④⑤
推论3
平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧
①④?②③⑤
或①⑤?②③④
O
C
D
A
B
P
在一个圆中,圆心到弦的垂线段的长度(或圆心到弦的距离),叫做弦心距。
半径、弦心距、弦长之间的数量关系:半径2=弦心距2+弦长????????。
——垂径定理
第2章对称图形——圆
教学目标
01
掌握圆的垂径定理的证明与运用
02
掌握圆的垂径定理的三个推论的证明与运用
垂径定理
01
二、定义
情境引入
请同学们完成以下操作 ,并回答问题:
Q1:画?O和?O的直径AB、弦CD,使AB⊥CD,垂足为P;
?
O
C
D
A
B
P
二、定义
Q2:在所画图中有哪些相等的线段、相等的弧?
O
C
A
B
P
D
(D)
由翻折可知:PC=PD,????????=????????,????????=????????。
?
01
二、定义
情境引入
Q3:是否还有其他的方法证明:PC=PD,????????=????????,????????=?????????
?
已知:AB是?O的直径,CD是?O的弦,AB⊥CD,垂直为P。
?
O
C
D
A
B
P
解:如图,连接OC、OD,
在Rt△OCP和Rt△ODP中,
????????=????????????????=????????,
∴△OPC?△OPD(HL),
?
∴PC=PD,∠BOC=∠BOD,
∴????????=????????,∠AOC=∠AOD,
∴????????=????????。
?
01
二、定义
情境引入
02
二、定义
知识精讲
垂径定理
垂直于弦的直径平分弦以及弦所对的两条弧。
O
C
D
A
B
P
符号语言(知二推三):
AB过圆心(AB为?O的直径),AB⊥CD
?PC=PD,????????=????????,????????=????????。
?
02
二、定义
知识精讲
弦心距
在一个圆中,圆心到弦的垂线段的长度(或圆心到弦的距离),叫做弦心距。
O
C
D
P
eg:OP的长度
02
二、定义
知识精讲
小明老师有几个问题想问大家
解:设?O的半径为r,
∵CD是?O的弦,OP⊥CD于点P,
∴CP=DP=????????CD(垂径定理),
在Rt△OPC中,OC2=OP2+CP2,
∴r2=OP2+????????CD2。
?
O
C
D
P
Q1:已知:OC是?O的半径,CD是?O的弦,OP⊥CD于点P,问:OC、OP、CD之间的数量关系?
?
02
二、定义
知识精讲
O
C
D
P
半径
弦心距
弦长的一半
半径、弦心距、弦长之间的数量关系:半径2=弦心距2+弦长????????。
?
02
二、定义
知识精讲
解:设?O的半径为r,
∵CD是?O的弦,OP⊥CD于点P,
∴CP=DP=????????CD(垂径定理),
∵OP=r-BP,
在Rt△OPC中,OC2=OP2+CP2,
∴r2=(r-BP)2+(????????CD)2。
?
Q2:已知:OB、OC是?O的半径,CD是?O的弦,OB⊥CD,垂足为P,问:OC、BP、CD之间的数量关系?
?
O
C
D
P
B
例1、(1)在以点为圆心的两个同心圆中,大圆的弦AB交小圆于点C、D。AC与BD相等吗?为什么?
03
典例精析
O
B
D
A
C
解:如图,过点O作OP⊥AB,垂足为P,
∵OP⊥AB,
∴AP=BP,CP=DP(垂径定理),
∴AP-CP=BP-DP,
即AC=BD.
P
例1、(2)AB、CD是?O的两条弦,AB∥CD。????????与????????相等吗?为什么?
?
03
典例精析
O
D
B
C
A
解:如图,作OQ⊥AB交?O于点Q,
∵OQ⊥AB,∴????????=????????(垂径定理),
又∵AB∥CD,
∴OQ⊥CD,∴????????=????????(垂径定理),
∴????????-????????=????????-????????,即????????=????????.
?
Q
例2、如图,点C是?O的弦AB上一点.若AC=6,BC=2,AB的弦心距为3,则OC的长为_________.
?
03
典例精析
解:如图,作OD⊥AB,垂足为D,
由题意可知:OD=3,
∵OD⊥AB,
∴BD=????????AB=????????(AC+BC)=4(垂径定理),
∴CD=BD-BC=2,
在Rt△OCD中,OC2=CD2+OD2=22+32=13,
∴OC=????????.
?
????????
?
D
例3、如图,AB是?O的直径,弦CD⊥AB于点E,若CD=6,AB=10,则AE的长为( )
A.1 B.2 C.3 D.4
?
03
典例精析
解:如图,连接OC,
在Rt△OCE中,OC2=CE2+OE2,
∵AB是?O的直径,AB=10,∴OC=5,
∵CD⊥AB ,∴CE=????????CD=3(垂径定理),
∴52=32+OE2,解得:OE=4,
∴AE=OA-OE=5-4=1.
?
A
例4、(1)如图,?O的直径AB垂直弦CD于点P,且P为半径OB的中点,若CD=6,则?O的半径长为_________.
?
03
典例精析
解:如图,连接OD,设?O的半径为r,
在Rt△ODP中,OD2=OP2+DP2,
∵P为半径OB的中点,∴OP=????????r,
∵?O的直径AB垂直弦CD于点P ,
∴DP=????????CD=3(垂径定理),
∴r2=(????????r)2+32,解得:r=2????.
?
2????
?
例4、(2)如图,AB是?O的直径,弦CD⊥AB 于E,若CD=4????,BE=2,则AB的长是_________.
?
03
典例精析
解:如图,连接OC,设?O的半径为r,
在Rt△OEC中,OC2=OE2+CE2,
∵BE=2,∴OE=r-2,
∵AB是?O的直径,CD⊥AB ,
∴CE=????????CD=2????(垂径定理),
∴r2=(r-2)2+(2????)2,解得:r=6,∴AB=2r=12.
?
12
垂径定理的推论
一、若已知:AB是?O的直径,CD是?O的弦,AB平分CD交CD于点P,能否推出:AB⊥CD,????????=????????,????????=?????????
?
02
二、定义
知识精讲
解:如图,连接OC、OD,
在△OPC和△OPD中,
????????=????????????????=????????????????=????????,
∴△OPC?△OPD(SSS),
?
O
C
D
A
B
P
∴∠APC=∠APD,
即AB⊥CD,
根据垂径定理:
∴????????=????????,????????=????????。
?
02
二、定义
知识精讲
垂径定理的推论1
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
O
C
D
A
B
P
符号语言(知二推三):
AB过圆心(AB为?O的直径),PC=PD
?AB⊥CD,????????=????????,????????=????????。
?
02
二、定义
知识精讲
垂径定理的推论1
注意:若此处的弦CD是直径,则结论不一定成立。
O
C
D
A
B
P
O
C
D
A
B
P
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
二、若已知:AB、CD是?O的弦,AB垂直平分CD交CD于点P,能否推出:AB过圆心,????????=????????,????????=?????????
?
02
二、定义
知识精讲
解:如图,连接OC、OD,
∵OC=OD,
∴O在CD的垂直平分线上,
即O在AB上,
∴AB过圆心(AB为?O的直径),
?
O
C
D
A
B
P
根据垂径定理或推论1:
∴????????=????????,????????=????????。
?
02
二、定义
知识精讲
垂径定理的推论2
弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
O
C
D
A
B
P
符号语言(知二推三):
AB⊥CD,PC=PD
?AB过圆心(AB为?O的直径),????????=????????,????????=????????。
?
三、(1)若已知:AB是?O的直径,????????=????????,连接CD交于AB点P,能否推出:AB⊥CD,PC=PD,????????=?????????
?
02
二、定义
知识精讲
解:如图,连接OC、OD、BC、BD,
∵AB是?O的直径,????????=????????,
∴BC=BD,????????-????????=????????-????????,即????????=????????,
又∵OC=OD,
∴AB垂直平分CD,
∴AB⊥CD,PC=PD。
?
O
C
D
A
B
P
三、(2)若已知:AB是?O的直径,????????=????????,连接CD交于AB点P,能否推出:AB⊥CD,PC=PD,????????=?????????
?
02
二、定义
知识精讲
解:连接OC、OD、BC、BD,
∵AB是?O的直径,????????=????????,
∴????????-????????=????????-????????,即????????=????????,
∴BC=BD,
?
O
C
D
A
B
P
又∵OC=OD,
∴AB垂直平分CD,
∴AB⊥CD,PC=PD。
02
二、定义
知识精讲
圆心角、弧、弦的关系
垂径定理的推论3
平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧。
符号语言(知二推三):
(1)AB过圆心(AB为?O的直径),????????=????????,
?AB⊥CD,PC=PD,????????=????????;
(2)AB过圆心(AB为?O的直径),????????=????????,
?AB⊥CD,PC=PD,????????=????????。
?
O
C
D
A
B
P
02
二、定义
知识精讲
圆心角、弧、弦的关系
垂径定理及其推论
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}①AB过圆心(AB为O的直径),②AB⊥CD,③PC=PD,④=,⑤=(知二推三)
文字语言
符号语言
垂径定理
垂直于弦的直径平分弦以及弦所对的两条弧
①②?③④⑤
推论1
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧
①③?②④⑤
推论2
弦的垂直平分线经过圆心,并且平分弦所对的两条弧
②③?①④⑤
推论3
平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧
①④?②③⑤
或①⑤?②③④
O
C
D
A
B
P
例1、如图,OA,OB,OC都是?O的半径,AC,OB交于点D.若AD=CD=8,OD=6,则BD的长为( )
A.5 B.4 C.3 D.2
?
03
典例精析
解:∵OB是?O的半径,AD=CD=8,
∴OB⊥AC(推论1),
在Rt△AOD中,OA2=AD2+OD2=82+62=100,
∴OA=10,∴OB=10,
∴BD=10-6=4.
?
B
例2、(1)如图,M是CD的中点,EM⊥CD,若CD=4,EM=6,则弧CED所在圆的半径为_________.
03
典例精析
解:设弧CED所在圆的半径为r,
∵M是CD的中点,EM⊥CD,
∴EM过圆心O,CM=????????CD=2(推论2),
如图,连接OC,
∵EM=6,∴OM=6-r,
在Rt△OCM中,OC2=CM2+OM2,即r2=22+(6-r)2,解得:r=????????????.
?
????????????
?
例2、(2)如图,在平面直角坐标系中,过格点A,B,C作一圆弧,则该弧的圆心的坐标为_________.
03
典例精析
解:如图,分别作弦AB、AC的垂直平分线,
设两条垂直平分线的交点为D,
根据垂径定理的推论2,点D即所求,坐标为:(2,0).
(2,0)
D
课后总结
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}①AB过圆心(AB为O的直径),②AB⊥CD,③PC=PD,④=,⑤=(知二推三)
文字语言
符号语言
垂径定理
垂直于弦的直径平分弦以及弦所对的两条弧
①②?③④⑤
推论1
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧
①③?②④⑤
推论2
弦的垂直平分线经过圆心,并且平分弦所对的两条弧
②③?①④⑤
推论3
平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧
①④?②③⑤
或①⑤?②③④
O
C
D
A
B
P
在一个圆中,圆心到弦的垂线段的长度(或圆心到弦的距离),叫做弦心距。
半径、弦心距、弦长之间的数量关系:半径2=弦心距2+弦长????????。
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
