9.2 代数式 课件(21张PPT)
图片预览








文档简介
(共21张PPT)
第九章 整式
第1节 整式的概念
9.2 代数式
1.理解代数式的概念,能够进行简单的代数式判别;
2.初步掌握列代数式的方法,能根据题目要求,正确列出相应的代数式;
3.经历列代数式的过程,再次体验字母表示数的数学思想,初步掌握文字语言与数学式子之间的转换。
在上节中10a、πr 、5(x-3)、 等,这些用字母表示数的式子都是由运算符号、括号、数、字母连接而成的,它能简明地表示数量关系。
用运算符号和括号把数或表示数的字母连接而成的式子叫做代数式(algebraic expression).
注意:单独一个数或者一个字母也是代数式,如 、0、x、h等。
教材例题
例1 用代数式表示:
(1)比a的3倍还多2的数
(2)b的一倍的相反数;
(3)a的平方的倒数减去一的差
(4) 9减去y的一的差;
(5)x的立方与2的和.
4
3
12
13
解:3a+2
解:
解:
解:
解:
列代数式时,用字母“代替”数字,应顺着文字语言叙述的顺序,用符
号语言表示数量关系.如第(1)小题中,“a的3倍”,用符号语言表示为
“3a”;“多 2”即比“3a”多“2”,因此是“3a十2”.此处要注意有些
文字的顺序,如第(4)小题,“9减去y的一的差”,如果改成“9 减去y 的
差的一”,结果就不一样了.
1
3
1
3
名师点拨:
设甲数是m,乙数是n,用代数式表示:
(1)甲乙两数的和的5倍;
(2) 甲减去乙的差与甲的相反数的积
(3)甲乙两数平方的和;
(4)甲乙两数和的立方
例2
解:(1)5(m+n)
(2)(m-n)·(-m)
(3)m +n
(4)(m+n)
教材例题
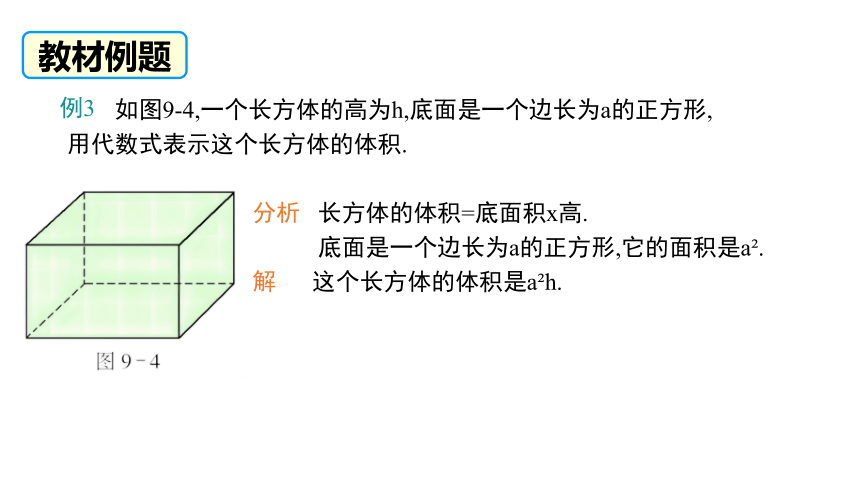
如图9-4,一个长方体的高为h,底面是一个边长为a的正方形,
用代数式表示这个长方体的体积.
分析 长方体的体积=底面积x高.
底面是一个边长为a的正方形,它的面积是a .
解 这个长方体的体积是a h.
例3
教材例题
本题是一个列代数式在实际中的运用问题.若设
体积为 V,则V=a h,这是公式,而此公式的两边都
是代数式。
名师点拨
典例精析
(2022年湖南长沙中考)为落实“双减”政策,某校利用课后服务开展了主题为“书香满校园”的读书活动.现需购买甲,乙两种读本共100本供学生阅读,其中甲种读本的单价为10元/本,乙种读本的单价为8元/本,设购买甲种读本x本,则购买乙种读本的费用为( )
A.8 元 B.10(100 )元 C.8(100 )元 D.(100 8 )元
【答案】C
【分析】根据题意列求得购买乙种读本 100 本,根据单价乘以数量即可求解.
【详解】解:设购买甲种读本x本,则购买乙种读本 100 本,乙种读本的单价为8元/本,则则购买乙种读本的费用为8(100 )元
变式训练
变式训练
典例精析
变式训练
变式训练
典例精析
变式训练
变式训练
1.用代数式表示:
(1)比a的2倍还少3的数;
(2)a与b的差的平方;
(3)x的2倍与y的一的差
(4)m与n的平方差
2.小明妈妈买了国库券a元,年利率为p%,一年到期利息是多少 本利和是多少
1
5
解:(1) 2a-3
解:(2) (a-b)
解:(3) 2x-一y
1
5
解:(4) m -n
解:ap%,a+p%
3.铅笔的单价是a元,钢笔的单价是b元,小明买了x支铅笔和y支钢笔,总共应付多少元
4.某商场进行换季打折销售,上衣按原价a元的3折销售,长裤按原价b元的对折销售,小明的妈妈买了3套打折服装,共要付多少元
解:ax+by
解:3(30%a+50%b)
1. 单独一个数或者一个字母也是代数式
2.带有“<(≤)”“>(≥)”“=”“≠”等符号的式子不是代数式,代数式中不含等号和不等号.如t=一不是代数式,但t和一都是代数式。
s
v
s
v
3.列代数式的方法方法:
(1)抓关键性词语,如“大”“小”“多”“少”“和”“差”“积”“商”“倍”等,弄清题目中的量及各量之间的关系;
(2)理清运算顺序,通常按照“先读先写”的顺序列式;
(3)对层次较多的题目,采取“浓缩原题,隔段处理,最后组装”的方式来处理;
(4)正确地运用括号,先括号内后括号外;先小括号,再中括号,最后大括号。
3. 列代数式的常见语句表示:
(1)a,b两数平方的和: a +b
(2)a,b两数和的平方:(a+b)
(3)a与b的平方的和:a+b
(4)a,b两数倒数的和:一+一
(5)a,b两数和的倒数:——
(6)a与b的倒数的和:a+一
(7)a,b两数绝对值的和:丨a丨+丨b丨
(8)a,b两数和的绝对值:丨a+b丨
1 1
a b
1
a+b
1
b
第九章 整式
第1节 整式的概念
9.2 代数式
1.理解代数式的概念,能够进行简单的代数式判别;
2.初步掌握列代数式的方法,能根据题目要求,正确列出相应的代数式;
3.经历列代数式的过程,再次体验字母表示数的数学思想,初步掌握文字语言与数学式子之间的转换。
在上节中10a、πr 、5(x-3)、 等,这些用字母表示数的式子都是由运算符号、括号、数、字母连接而成的,它能简明地表示数量关系。
用运算符号和括号把数或表示数的字母连接而成的式子叫做代数式(algebraic expression).
注意:单独一个数或者一个字母也是代数式,如 、0、x、h等。
教材例题
例1 用代数式表示:
(1)比a的3倍还多2的数
(2)b的一倍的相反数;
(3)a的平方的倒数减去一的差
(4) 9减去y的一的差;
(5)x的立方与2的和.
4
3
12
13
解:3a+2
解:
解:
解:
解:
列代数式时,用字母“代替”数字,应顺着文字语言叙述的顺序,用符
号语言表示数量关系.如第(1)小题中,“a的3倍”,用符号语言表示为
“3a”;“多 2”即比“3a”多“2”,因此是“3a十2”.此处要注意有些
文字的顺序,如第(4)小题,“9减去y的一的差”,如果改成“9 减去y 的
差的一”,结果就不一样了.
1
3
1
3
名师点拨:
设甲数是m,乙数是n,用代数式表示:
(1)甲乙两数的和的5倍;
(2) 甲减去乙的差与甲的相反数的积
(3)甲乙两数平方的和;
(4)甲乙两数和的立方
例2
解:(1)5(m+n)
(2)(m-n)·(-m)
(3)m +n
(4)(m+n)
教材例题
如图9-4,一个长方体的高为h,底面是一个边长为a的正方形,
用代数式表示这个长方体的体积.
分析 长方体的体积=底面积x高.
底面是一个边长为a的正方形,它的面积是a .
解 这个长方体的体积是a h.
例3
教材例题
本题是一个列代数式在实际中的运用问题.若设
体积为 V,则V=a h,这是公式,而此公式的两边都
是代数式。
名师点拨
典例精析
(2022年湖南长沙中考)为落实“双减”政策,某校利用课后服务开展了主题为“书香满校园”的读书活动.现需购买甲,乙两种读本共100本供学生阅读,其中甲种读本的单价为10元/本,乙种读本的单价为8元/本,设购买甲种读本x本,则购买乙种读本的费用为( )
A.8 元 B.10(100 )元 C.8(100 )元 D.(100 8 )元
【答案】C
【分析】根据题意列求得购买乙种读本 100 本,根据单价乘以数量即可求解.
【详解】解:设购买甲种读本x本,则购买乙种读本 100 本,乙种读本的单价为8元/本,则则购买乙种读本的费用为8(100 )元
变式训练
变式训练
典例精析
变式训练
变式训练
典例精析
变式训练
变式训练
1.用代数式表示:
(1)比a的2倍还少3的数;
(2)a与b的差的平方;
(3)x的2倍与y的一的差
(4)m与n的平方差
2.小明妈妈买了国库券a元,年利率为p%,一年到期利息是多少 本利和是多少
1
5
解:(1) 2a-3
解:(2) (a-b)
解:(3) 2x-一y
1
5
解:(4) m -n
解:ap%,a+p%
3.铅笔的单价是a元,钢笔的单价是b元,小明买了x支铅笔和y支钢笔,总共应付多少元
4.某商场进行换季打折销售,上衣按原价a元的3折销售,长裤按原价b元的对折销售,小明的妈妈买了3套打折服装,共要付多少元
解:ax+by
解:3(30%a+50%b)
1. 单独一个数或者一个字母也是代数式
2.带有“<(≤)”“>(≥)”“=”“≠”等符号的式子不是代数式,代数式中不含等号和不等号.如t=一不是代数式,但t和一都是代数式。
s
v
s
v
3.列代数式的方法方法:
(1)抓关键性词语,如“大”“小”“多”“少”“和”“差”“积”“商”“倍”等,弄清题目中的量及各量之间的关系;
(2)理清运算顺序,通常按照“先读先写”的顺序列式;
(3)对层次较多的题目,采取“浓缩原题,隔段处理,最后组装”的方式来处理;
(4)正确地运用括号,先括号内后括号外;先小括号,再中括号,最后大括号。
3. 列代数式的常见语句表示:
(1)a,b两数平方的和: a +b
(2)a,b两数和的平方:(a+b)
(3)a与b的平方的和:a+b
(4)a,b两数倒数的和:一+一
(5)a,b两数和的倒数:——
(6)a与b的倒数的和:a+一
(7)a,b两数绝对值的和:丨a丨+丨b丨
(8)a,b两数和的绝对值:丨a+b丨
1 1
a b
1
a+b
1
b
