24.5 相似三角形的性质 课件(43张PPT)
文档属性
| 名称 | 24.5 相似三角形的性质 课件(43张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 22.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 10:08:30 | ||
图片预览





文档简介
(共43张PPT)
24.5相似三角形的性质
第24章 相似三角形
沪教版 九年级第一学期
相似三角形对应高、角平分线、中线的比
相似三角形对应面积的比
相似三角形对应周长的比
01
03
02
CONTANTS
目 录
相似三角形对应高、角平分线、中线的比
01
A
C
B
A1
C1
B1
问题1: △ABC与△A1B1C1相似吗?
回顾引入
A
C
B
A1
C1
B1
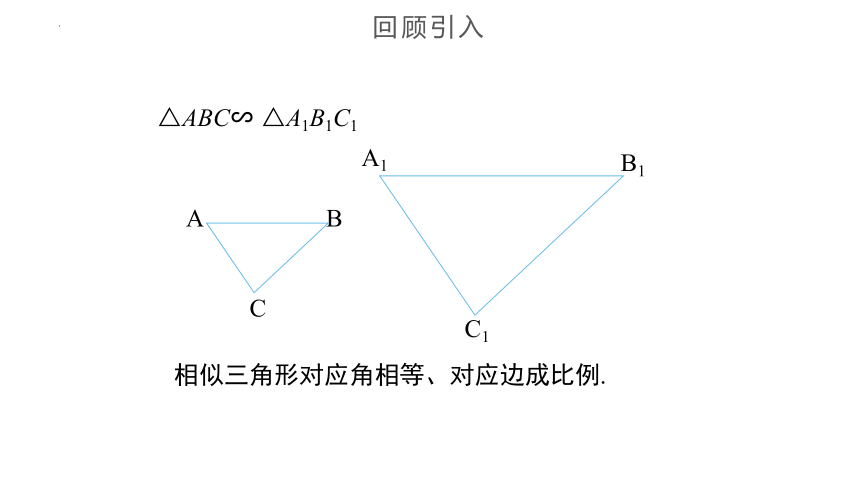
相似三角形对应角相等、对应边成比例.
△ABC∽ △A1B1C1
回顾引入
思考:三角形中,除了角度和边长外,还有哪些几何量?
高、角平分线、中线的长度,周长、面积等
高
角平分线
中线
问题引入
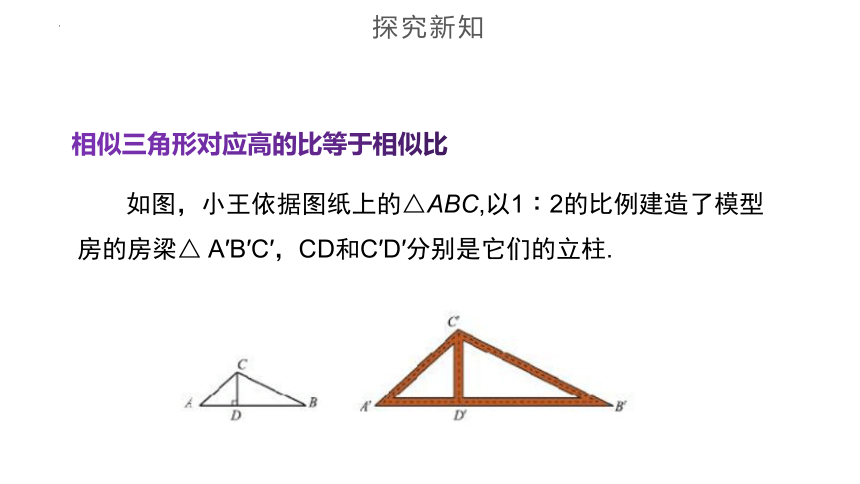
如图,小王依据图纸上的△ABC,以1︰2的比例建造了模型房的房梁△ A′B′C′,CD和C′D′分别是它们的立柱.
探究新知
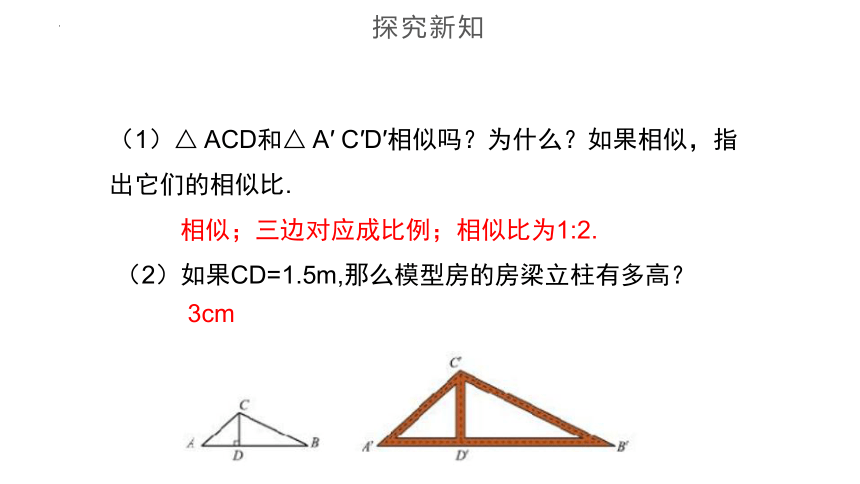
(1)△ ACD和△ A′ C′D′相似吗?为什么?如果相似,指出它们的相似比.
(2)如果CD=1.5m,那么模型房的房梁立柱有多高?
相似;三边对应成比例;相似比为1:2.
3cm
探究新知
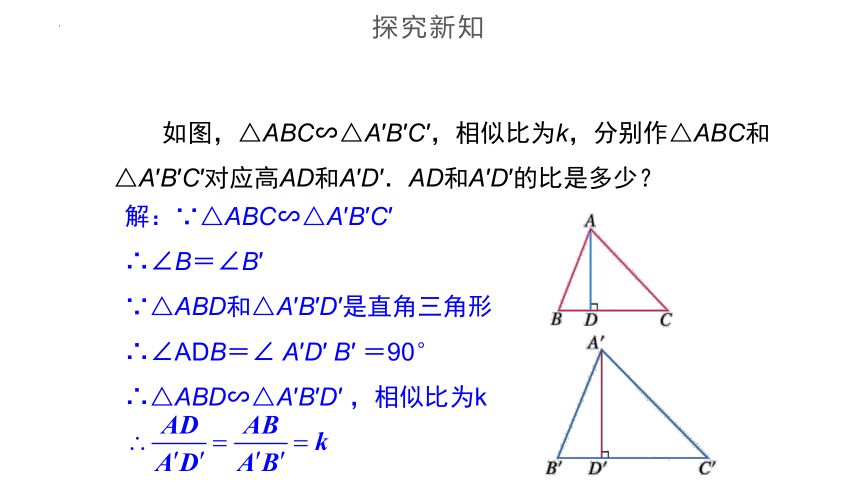
如图,△ABC∽△A′B′C′,相似比为k,分别作△ABC和△A′B′C′对应高AD和A′D′.AD和A′D′的比是多少?
解:∵△ABC∽△A′B′C′
∴∠B=∠B′
∵△ABD和△A′B′D′是直角三角形
∴∠ADB=∠ A′D′ B′ =90°
∴△ABD∽△A′B′D′ ,相似比为k
探究新知
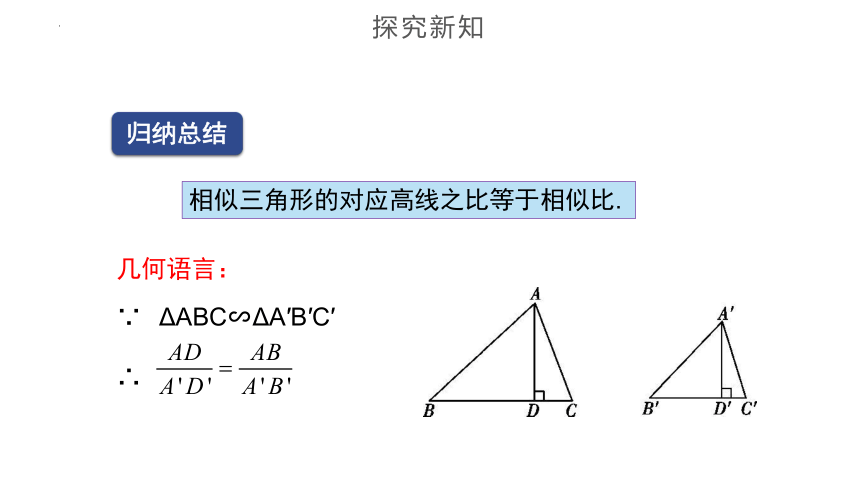
归纳总结
相似三角形的对应高线之比等于相似比.
ΔABC∽ΔA′B′C′
∵
∴
几何语言:
探究新知
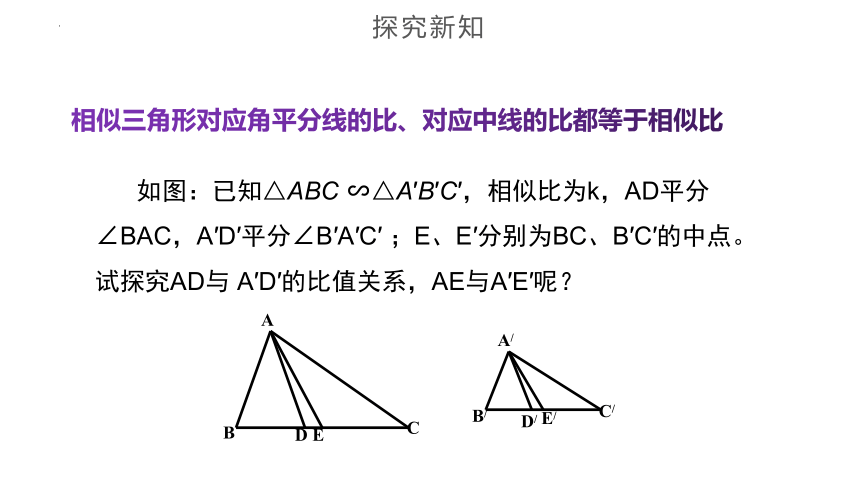
如图:已知△ABC ∽△A′B′C′,相似比为k,AD平分∠BAC,A′D′平分∠B′A′C′ ;E、E′分别为BC、B′C′的中点。试探究AD与 A′D′的比值关系,AE与A′E′呢?
A
B
C
D
E
A/
B/
C/
D/
E/
探究新知
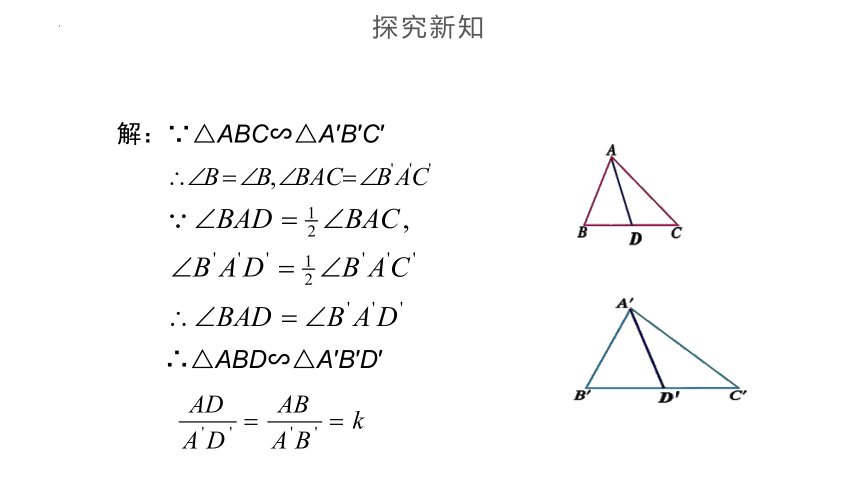
解:∵△ABC∽△A′B′C′
∴△ABD∽△A′B′D′
探究新知
A
B
C
E
A/
B/
C/
E/
解:∵△ABC∽△A′B′C′
∴△ABE∽△A′B′E′
探究新知
归纳总结
相似三角形对应高的比,对应角平分线的比,对应中线的比都等于相似比。
∵△ABC∽△A′B′C′
几何语言:
探究新知
对应高的比
对应中线的比
对应角平分线的比
相
似
三
角
形
都等于相似比.
归纳总结
注意:相似比是有顺序的,不能颠倒相似三角形中元素的顺序。
探究新知
1 已知△ABC∽△DEF,若△ABC 与△DEF 的相似比为 ,则△ABC 与△DEF 对应中线的比为( )
A. B. C. D.
A
2 如图,已知△ADE∽△ABC,相似比为2∶5,则AF∶AG 为( )
A.2∶5
B.5∶2
C.5∶1
D.1∶5
A
巩固练习
如图,在△ABC 中,AD⊥BC,垂足为D,EF∥BC,分别交AB,AC,AD 于点E,F,G, AD=15,求AG 的长.
∵EF∥BC,∴△AEF∽△ABC.
∵AD⊥BC,∴ AD⊥EF.
∴
又∵ AD=15,∴
∴ AG=9.
例题1
解:
典型例题
相似三角形对应周长的比
02
问题
某施工队在道路拓宽施工时遇到这样一个问题,马路旁边原有一个面积为100平方米,周长为80米的三角形绿化地,由于马路拓宽绿地被削去了一个角,变成了一个梯形,原绿化地一边AB的长由原来的30米缩短成18米. 现在的问题是:它的周长是多少?
探究新知
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC,
∴ 由比例的性质可
解:
将上面生活中的问题转化为数学问题是:
如图,已知DE∥BC,AB=30m,BD=18m,△ABC
的周长为80m,求△ADE 的周长.
探究新知
又∵△ADE 的周长=AD+AE+DE,
△ABC 的周长=AB+AC+BC,
∴
∴△ADE 的周长=32米.
探究新知
总结:相似三角形周长的比等于相似比.
如图,在Rt△ABC 中,∠ACB=90°,∠A=30°,CD⊥AB于点D,则△BCD与△ABC 的周长之比为( )
A.1∶2
B.1∶3
C.1∶4
D.1∶5
例题2
A
典型例题
导引:
在Rt△ABC 中,∠A+∠B=90°;
在Rt△BCD 中,∠BCD+∠B=90°,
所以∠BCD=∠A.
又因为∠B=∠B,所以△BCD∽△BAC.
在Rt△ABC 中,∠A=30°,
所以 则△BCD与△ABC 的周长比等于相
似比
探究新知
相似三角形周长的比等于相似比在解题时,如果是相似图形求周长就常用到周长比等于相似比.
探究新知
1. △ABC 与△DEF 的相似比为1∶4,则△ABC 与△DEF 的周长比为( )
A.1∶2 B.1∶3
C.1∶4 D.1∶16
C
2. 已知△ABC∽△DEF,相似比为3∶1,且△ABC 的周长为18,则△DEF 的周长为( )
A.2 B.3
C.6 D.54
C
巩固练习
相似三角形对应面积的比
03
问题
相似三角形面积的比,与它们的相似比之间有什么关系呢?
探究新知
如图,△ABC∽△A′B′C′,相似比为k,AD、A′D′ 分别为BC,B′C′边上的高.
(1)△ABC的面积和△A′B′C′的面积的比与他们的相似比有什么关系 请说明理由.
探究新知
因为
所以
即△ABC与△A′B′C′的面积之比等于相似比的平方.
探究新知
相似三角形面积的比等于相似比的平方.
注意:学会此性质的逆用。
探究新知
如图,在△ABC 中,D,E,F分别为BC,AC,AB 边的中点. 求:
(1)△DEF 的周长与△ABC 的周长之比.
(2)△DEF 的面积与△ABC 的面积之比.
例题3
典型例题
解:
∵D,E,F分别为BC,AC,AB 的中点,
∴ DE∥AB, EF∥BC,DF∥AC,
∴△DEF∽△ABC.
∴△DEF 的周长与△ABC 的周长之比为1∶2,
△DEF 的面积与△ABC 的面积之比为1∶4.
典型例题
A
C
课堂练习
C
课堂练习
B
课堂练习
D
课堂练习
6.如图,在△ABC中DE∥BC,AD=3BD, S△ABC=48. 求S△ADE.
解:∵DE∥BC
∴△ADE∽△ABC
∴
∴
课堂练习
7.如图,AD是△ABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=60cm,AD=40cm,四边形PQRS是正方形.求正方形PQRS的边长.
解:四边形PQRS是正方形
∴SR∥BC
∴△ASR∽△ABC
∴
设正方形PQRS的边长为xcm,则AE=(40-x)cm.即 ,解得x=24
正方形PQRS的边长为24cm.
课堂练习
8.如图,点E是正方形ABCD的边DC的中点,以AE为边作正方形AEHG, HE与BC交于点Q,连接AQ.
(1)求证:△ADE∽△ECQ;
(2)设S△CEQ=S1, S△AED=S2, S△EAQ=S3, 求证:S1+S2=S3.
证明:∵四边形ABCD与四边形AEHG是正方形∴∠ADE=∠ECQ=90°,∠AEH=90°
∴∠AED+∠DAE=90°,∠AED+∠CEQ=90°
∴∠DAE=∠CEQ
∴△ADE∽△ECQ
课堂练习
(2)设S△CEQ=S1, S△AED=S2, S△EAQ=S3, 求证:S1+S2=S3.
证明:∵△ADE∽△ECQ
∴
∵DE=CE,
∴
∵∠AEG=∠ECQ=90°
∴△AEQ∽△ECQ
∴△AEQ∽△ECQ∽△ADE
∴
课堂练习
(2)设S△CEQ=S1, S△AED=S2, S△EAQ=S3, 求证:S1+S2=S3.
∴
∵
∴
∴
课堂练习
相似三角形的性质
相似三角形对应高的比等于相似比
相似三角形对应角平分线的比等于相似比
相似三角形对应中线的比等于相似比
相似三角形对应周长的比等于相似比
相似三角形对应面积的比等于相似比的平方
课堂小结
感谢观看
24.5相似三角形的性质
第24章 相似三角形
沪教版 九年级第一学期
相似三角形对应高、角平分线、中线的比
相似三角形对应面积的比
相似三角形对应周长的比
01
03
02
CONTANTS
目 录
相似三角形对应高、角平分线、中线的比
01
A
C
B
A1
C1
B1
问题1: △ABC与△A1B1C1相似吗?
回顾引入
A
C
B
A1
C1
B1
相似三角形对应角相等、对应边成比例.
△ABC∽ △A1B1C1
回顾引入
思考:三角形中,除了角度和边长外,还有哪些几何量?
高、角平分线、中线的长度,周长、面积等
高
角平分线
中线
问题引入
如图,小王依据图纸上的△ABC,以1︰2的比例建造了模型房的房梁△ A′B′C′,CD和C′D′分别是它们的立柱.
探究新知
(1)△ ACD和△ A′ C′D′相似吗?为什么?如果相似,指出它们的相似比.
(2)如果CD=1.5m,那么模型房的房梁立柱有多高?
相似;三边对应成比例;相似比为1:2.
3cm
探究新知
如图,△ABC∽△A′B′C′,相似比为k,分别作△ABC和△A′B′C′对应高AD和A′D′.AD和A′D′的比是多少?
解:∵△ABC∽△A′B′C′
∴∠B=∠B′
∵△ABD和△A′B′D′是直角三角形
∴∠ADB=∠ A′D′ B′ =90°
∴△ABD∽△A′B′D′ ,相似比为k
探究新知
归纳总结
相似三角形的对应高线之比等于相似比.
ΔABC∽ΔA′B′C′
∵
∴
几何语言:
探究新知
如图:已知△ABC ∽△A′B′C′,相似比为k,AD平分∠BAC,A′D′平分∠B′A′C′ ;E、E′分别为BC、B′C′的中点。试探究AD与 A′D′的比值关系,AE与A′E′呢?
A
B
C
D
E
A/
B/
C/
D/
E/
探究新知
解:∵△ABC∽△A′B′C′
∴△ABD∽△A′B′D′
探究新知
A
B
C
E
A/
B/
C/
E/
解:∵△ABC∽△A′B′C′
∴△ABE∽△A′B′E′
探究新知
归纳总结
相似三角形对应高的比,对应角平分线的比,对应中线的比都等于相似比。
∵△ABC∽△A′B′C′
几何语言:
探究新知
对应高的比
对应中线的比
对应角平分线的比
相
似
三
角
形
都等于相似比.
归纳总结
注意:相似比是有顺序的,不能颠倒相似三角形中元素的顺序。
探究新知
1 已知△ABC∽△DEF,若△ABC 与△DEF 的相似比为 ,则△ABC 与△DEF 对应中线的比为( )
A. B. C. D.
A
2 如图,已知△ADE∽△ABC,相似比为2∶5,则AF∶AG 为( )
A.2∶5
B.5∶2
C.5∶1
D.1∶5
A
巩固练习
如图,在△ABC 中,AD⊥BC,垂足为D,EF∥BC,分别交AB,AC,AD 于点E,F,G, AD=15,求AG 的长.
∵EF∥BC,∴△AEF∽△ABC.
∵AD⊥BC,∴ AD⊥EF.
∴
又∵ AD=15,∴
∴ AG=9.
例题1
解:
典型例题
相似三角形对应周长的比
02
问题
某施工队在道路拓宽施工时遇到这样一个问题,马路旁边原有一个面积为100平方米,周长为80米的三角形绿化地,由于马路拓宽绿地被削去了一个角,变成了一个梯形,原绿化地一边AB的长由原来的30米缩短成18米. 现在的问题是:它的周长是多少?
探究新知
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC,
∴ 由比例的性质可
解:
将上面生活中的问题转化为数学问题是:
如图,已知DE∥BC,AB=30m,BD=18m,△ABC
的周长为80m,求△ADE 的周长.
探究新知
又∵△ADE 的周长=AD+AE+DE,
△ABC 的周长=AB+AC+BC,
∴
∴△ADE 的周长=32米.
探究新知
总结:相似三角形周长的比等于相似比.
如图,在Rt△ABC 中,∠ACB=90°,∠A=30°,CD⊥AB于点D,则△BCD与△ABC 的周长之比为( )
A.1∶2
B.1∶3
C.1∶4
D.1∶5
例题2
A
典型例题
导引:
在Rt△ABC 中,∠A+∠B=90°;
在Rt△BCD 中,∠BCD+∠B=90°,
所以∠BCD=∠A.
又因为∠B=∠B,所以△BCD∽△BAC.
在Rt△ABC 中,∠A=30°,
所以 则△BCD与△ABC 的周长比等于相
似比
探究新知
相似三角形周长的比等于相似比在解题时,如果是相似图形求周长就常用到周长比等于相似比.
探究新知
1. △ABC 与△DEF 的相似比为1∶4,则△ABC 与△DEF 的周长比为( )
A.1∶2 B.1∶3
C.1∶4 D.1∶16
C
2. 已知△ABC∽△DEF,相似比为3∶1,且△ABC 的周长为18,则△DEF 的周长为( )
A.2 B.3
C.6 D.54
C
巩固练习
相似三角形对应面积的比
03
问题
相似三角形面积的比,与它们的相似比之间有什么关系呢?
探究新知
如图,△ABC∽△A′B′C′,相似比为k,AD、A′D′ 分别为BC,B′C′边上的高.
(1)△ABC的面积和△A′B′C′的面积的比与他们的相似比有什么关系 请说明理由.
探究新知
因为
所以
即△ABC与△A′B′C′的面积之比等于相似比的平方.
探究新知
相似三角形面积的比等于相似比的平方.
注意:学会此性质的逆用。
探究新知
如图,在△ABC 中,D,E,F分别为BC,AC,AB 边的中点. 求:
(1)△DEF 的周长与△ABC 的周长之比.
(2)△DEF 的面积与△ABC 的面积之比.
例题3
典型例题
解:
∵D,E,F分别为BC,AC,AB 的中点,
∴ DE∥AB, EF∥BC,DF∥AC,
∴△DEF∽△ABC.
∴△DEF 的周长与△ABC 的周长之比为1∶2,
△DEF 的面积与△ABC 的面积之比为1∶4.
典型例题
A
C
课堂练习
C
课堂练习
B
课堂练习
D
课堂练习
6.如图,在△ABC中DE∥BC,AD=3BD, S△ABC=48. 求S△ADE.
解:∵DE∥BC
∴△ADE∽△ABC
∴
∴
课堂练习
7.如图,AD是△ABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=60cm,AD=40cm,四边形PQRS是正方形.求正方形PQRS的边长.
解:四边形PQRS是正方形
∴SR∥BC
∴△ASR∽△ABC
∴
设正方形PQRS的边长为xcm,则AE=(40-x)cm.即 ,解得x=24
正方形PQRS的边长为24cm.
课堂练习
8.如图,点E是正方形ABCD的边DC的中点,以AE为边作正方形AEHG, HE与BC交于点Q,连接AQ.
(1)求证:△ADE∽△ECQ;
(2)设S△CEQ=S1, S△AED=S2, S△EAQ=S3, 求证:S1+S2=S3.
证明:∵四边形ABCD与四边形AEHG是正方形∴∠ADE=∠ECQ=90°,∠AEH=90°
∴∠AED+∠DAE=90°,∠AED+∠CEQ=90°
∴∠DAE=∠CEQ
∴△ADE∽△ECQ
课堂练习
(2)设S△CEQ=S1, S△AED=S2, S△EAQ=S3, 求证:S1+S2=S3.
证明:∵△ADE∽△ECQ
∴
∵DE=CE,
∴
∵∠AEG=∠ECQ=90°
∴△AEQ∽△ECQ
∴△AEQ∽△ECQ∽△ADE
∴
课堂练习
(2)设S△CEQ=S1, S△AED=S2, S△EAQ=S3, 求证:S1+S2=S3.
∴
∵
∴
∴
课堂练习
相似三角形的性质
相似三角形对应高的比等于相似比
相似三角形对应角平分线的比等于相似比
相似三角形对应中线的比等于相似比
相似三角形对应周长的比等于相似比
相似三角形对应面积的比等于相似比的平方
课堂小结
感谢观看
