11.3三角形全等的条件(2)(SAS)-.[下学期]
文档属性
| 名称 | 11.3三角形全等的条件(2)(SAS)-.[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 206.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-05-22 00:00:00 | ||
图片预览





文档简介
课件16张PPT。11.3探索三角形全等的条件(1)
—SAS(边角边)你还记得吗?什么叫全等三角形?两个能完全重合的三角形叫做全等三角形。全等三角形的对应边、对应角有什么重要性质?全等三角形的对应边相等,对应角相等。 已知△ABC≌ △A’B’C’, △ABC的周长
为10cm,AB=3cm,BC=4cm,则:
A’B’= cm,B’C’= cm ,A’C’= cm.343 两个三角形,需要有多少组边或角对应相等时,才一定会全等呢?探索一个角对应相等的两个三角形不一定全等;一条边对应相等的两个三角形不一定全等;两个角对应相等的两个三角形不一定全等;两条边对应相等的两个三角形不一定全等;一个角和一条边对应相等的两个三角形不一定全等;3、再增加一个条件有哪几种情况?
(1)、两边一角;
(2)、两角一边;
(3)、边边边;
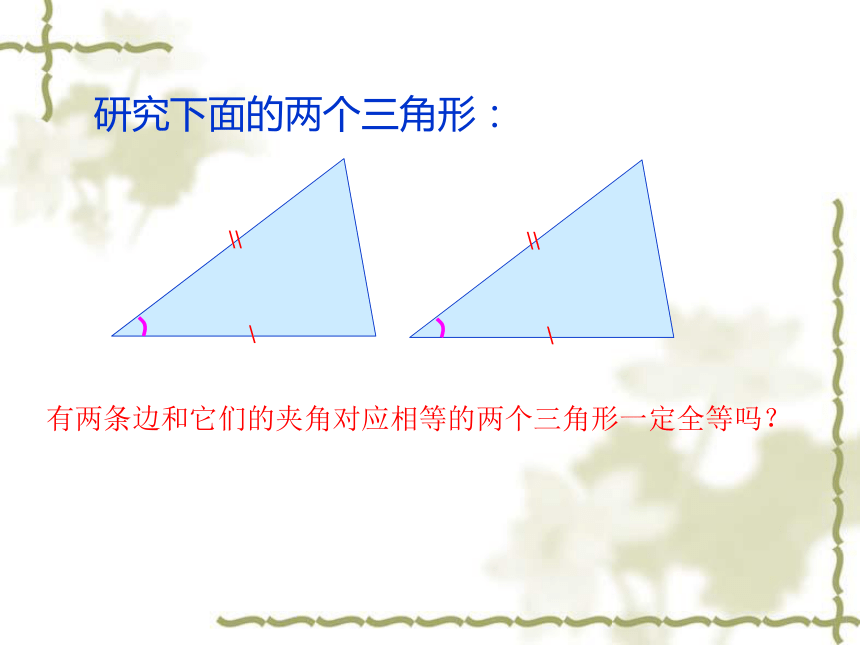
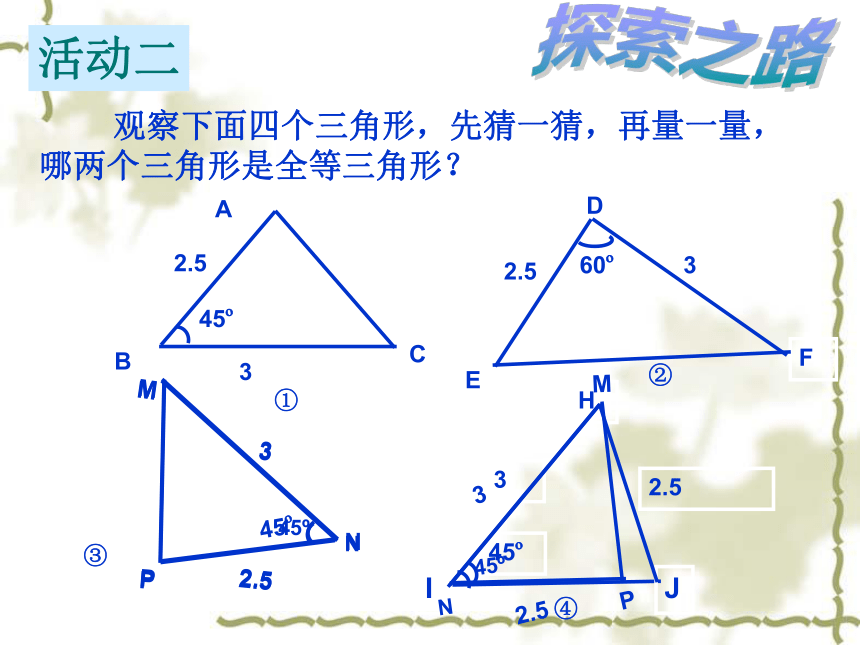
(4)、角角角这节课我们将研究第一种情况:两边一角 ?两组边和一组角分别相等的两个三角形全等吗?有两条边和它们的夹角对应相等的两个三角形一定全等吗?研究下面的两个三角形:活动一探索之路 每人用一张长方形纸剪一个直角 三角形,怎样才能使全班同学剪下的直角 三角形都全等呢? 2.5EFD360o探索之路 观察下面四个三角形,先猜一猜,再量一量,哪两个三角形是全等三角形?活动二2.5①②3H45oJ④I③2.5EFD360o探索之路 观察下面四个三角形,先猜一猜,再量一量,哪两个三角形是全等三角形?活动二2.5①②3H45oJ④I③大家一起做下面的实验:1、画∠MAN=45O;
2、在AM上截取AB=8cm;在AN上截取AC=6cm;
3、连接BC。
剪下所得的△ABC,与周围同学所剪的比较一下,它们全等吗?BC′活动三两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”拓展应用 1、如果两个三角形中有两边及其中一边的对角对应相等,这两个三角形全等吗?ABC5503.0cm2.5cmD5503.0cmEF2.5cm例题 如图:AB=AD,∠BAC= ∠DAC,△ABC和△ADC全等吗?为什么?△ABC≌ △ADC,
因为AB=AD∠BAC=∠DAC,AC=AC,
根据“SAS”,可以得到△ABC≌ △ADC,想一想:1、如图:AB=AC,AD=AE,△ABE和△ACD全等吗?请说明理由。△ABE≌ △ACD,
因为AB=AC∠BAE=∠CAD,AE=AD,
根据“SAS”,可以得到△ABE≌ △ACD,在这个图形中你还能得到哪些相等的线段和相等的角?练一练:练习巩固AB DC≌在△ABO和△DCO中,若AO=DO,只要再有
= , △ABO≌△DCOAC DBBO CO生活中的数学“五一”节期间,几名学生在公园,测量一池塘两端A,B的距离,设计了如下方案:如图,先在平地上取了一个可直接到达A,B的点C,再连接AC,BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测DE的长即为AB的距离,你认为这种方案可行吗?并加以说明.AE练习巩固通过这节课的学习你有什么收获?本节课你学习了什么?
发现了什么?
有什么收获?
还存在什么没有解决的问题?
为10cm,AB=3cm,BC=4cm,则:
A’B’= cm,B’C’= cm ,A’C’= cm.343 两个三角形,需要有多少组边或角对应相等时,才一定会全等呢?探索一个角对应相等的两个三角形不一定全等;一条边对应相等的两个三角形不一定全等;两个角对应相等的两个三角形不一定全等;两条边对应相等的两个三角形不一定全等;一个角和一条边对应相等的两个三角形不一定全等;3、再增加一个条件有哪几种情况?
(1)、两边一角;
(2)、两角一边;
(3)、边边边;
(4)、角角角这节课我们将研究第一种情况:两边一角 ?两组边和一组角分别相等的两个三角形全等吗?有两条边和它们的夹角对应相等的两个三角形一定全等吗?研究下面的两个三角形:活动一探索之路 每人用一张长方形纸剪一个直角 三角形,怎样才能使全班同学剪下的直角 三角形都全等呢? 2.5EFD360o探索之路 观察下面四个三角形,先猜一猜,再量一量,哪两个三角形是全等三角形?活动二2.5①②3H45oJ④I③2.5EFD360o探索之路 观察下面四个三角形,先猜一猜,再量一量,哪两个三角形是全等三角形?活动二2.5①②3H45oJ④I③大家一起做下面的实验:1、画∠MAN=45O;
2、在AM上截取AB=8cm;在AN上截取AC=6cm;
3、连接BC。
剪下所得的△ABC,与周围同学所剪的比较一下,它们全等吗?BC′活动三两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”拓展应用 1、如果两个三角形中有两边及其中一边的对角对应相等,这两个三角形全等吗?ABC5503.0cm2.5cmD5503.0cmEF2.5cm例题 如图:AB=AD,∠BAC= ∠DAC,△ABC和△ADC全等吗?为什么?△ABC≌ △ADC,
因为AB=AD∠BAC=∠DAC,AC=AC,
根据“SAS”,可以得到△ABC≌ △ADC,想一想:1、如图:AB=AC,AD=AE,△ABE和△ACD全等吗?请说明理由。△ABE≌ △ACD,
因为AB=AC∠BAE=∠CAD,AE=AD,
根据“SAS”,可以得到△ABE≌ △ACD,在这个图形中你还能得到哪些相等的线段和相等的角?练一练:练习巩固AB DC≌在△ABO和△DCO中,若AO=DO,只要再有
= , △ABO≌△DCOAC DBBO CO生活中的数学“五一”节期间,几名学生在公园,测量一池塘两端A,B的距离,设计了如下方案:如图,先在平地上取了一个可直接到达A,B的点C,再连接AC,BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测DE的长即为AB的距离,你认为这种方案可行吗?并加以说明.AE练习巩固通过这节课的学习你有什么收获?本节课你学习了什么?
发现了什么?
有什么收获?
还存在什么没有解决的问题?
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
