人教版高中数学选择性必修第一册3.2.2 第一课时 双曲线的简单几何性质 课件(共36张PPT)
文档属性
| 名称 | 人教版高中数学选择性必修第一册3.2.2 第一课时 双曲线的简单几何性质 课件(共36张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 06:05:15 | ||
图片预览











文档简介
(共36张PPT)
3.2.2 双曲线的简单几何性质
第一课时 双曲线的简单几何性质(1)
[学习目标]
1.掌握双曲线的简单几何性质.
2.理解双曲线离心率的定义、取值范围和渐近线方程.
必备知识 自主探究
关键能力 互动探究
课时作业 巩固提升
问题1 双曲线有哪些几何性质?
问题2 双曲线的离心率与双曲线的形状有怎样的联系?
A
C
3.双曲线y2-4x2=4的焦点坐标为_________________________.
4x±5y=0
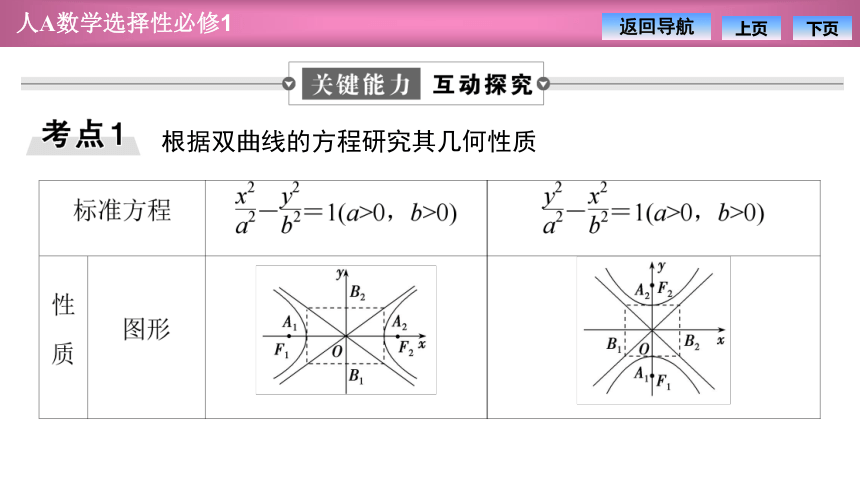
根据双曲线的方程研究其几何性质
(0,-c),(0,c)
x≤-a或x≥a,y∈R
A1(-a,0),A2(a,0)
A1(0,-a),A2(0,a)
2a
2b
a
b
[例1] 求双曲线4x2-y2=4的顶点坐标、焦点坐标、实半轴长、虚半轴长、离心率和渐近线方程,并作出草图.
分析:化标准方程,确定焦点位置,写出几何性质.
根据双曲线的标准方程可以得出双曲线的几何性质,双曲线的几何性质主要包括“六点”——两个实轴端点、两个虚轴端点、两个焦点;“四线”——两条对称轴、两条渐近线;“两比率”——离心率、渐近线的斜率.双曲线的实轴长、虚轴长、焦距、离心率只与双曲线的形状和大小有关,而与双曲线的位置无关.双曲线的实轴端点坐标、虚轴端点坐标、焦点坐标、渐近线方程不仅与双曲线的形状和大小有关,而且与双曲线的实轴位置有关.
1.求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程.
利用双曲线的几何性质求其标准方程
巧设双曲线方程的六种方法与技巧
(5)渐近线为y=kx(k≠0)的双曲线方程可设为 .
(6)渐近线为ax±by=0的双曲线方程可设为 .
k2x2-y2=λ(λ≠0)
a2x2-b2y2=λ(λ≠0)
根据双曲线的某些几何性质求双曲线的方程,一般用待定系数法转化为解方程(组),但要注意焦点的位置,从而正确选择方程的形式.利用待定系数法求双曲线标准方程的关键是设出双曲线方程的标准形式,根据已知条件,列出关于a,b,c的方程并求出a,b,c的值.
(3)利用方程求.若得到的是关于a,c的齐次方程,即p·c2+q·ac+r·a2=0(p,q,r为常数,且p≠0),则转化为关于e的方程 求解.
p·e2+q·e+r=0
2.求双曲线离心率的取值范围,通常构造不等式求得,特别注意双曲线离心率 .
e∈(1,+∞)
双曲线离心率的值或取值范围的求法
1.知识清单:(1)根据双曲线的方程研究其几何性质.
(2)利用双曲线的几何性质求其标准方程.
(3)求双曲线离心率的值或取值范围.
2.方法归纳:定义法、待定系数法、转化与化归.
3.常见误区:(1)忽略双曲线焦点位置.
(2)求双曲线或离心率时漏解.
(3)忽略双曲线离心率范围(1,+∞).
课时作业 巩固提升
3.2.2 双曲线的简单几何性质
第一课时 双曲线的简单几何性质(1)
[学习目标]
1.掌握双曲线的简单几何性质.
2.理解双曲线离心率的定义、取值范围和渐近线方程.
必备知识 自主探究
关键能力 互动探究
课时作业 巩固提升
问题1 双曲线有哪些几何性质?
问题2 双曲线的离心率与双曲线的形状有怎样的联系?
A
C
3.双曲线y2-4x2=4的焦点坐标为_________________________.
4x±5y=0
根据双曲线的方程研究其几何性质
(0,-c),(0,c)
x≤-a或x≥a,y∈R
A1(-a,0),A2(a,0)
A1(0,-a),A2(0,a)
2a
2b
a
b
[例1] 求双曲线4x2-y2=4的顶点坐标、焦点坐标、实半轴长、虚半轴长、离心率和渐近线方程,并作出草图.
分析:化标准方程,确定焦点位置,写出几何性质.
根据双曲线的标准方程可以得出双曲线的几何性质,双曲线的几何性质主要包括“六点”——两个实轴端点、两个虚轴端点、两个焦点;“四线”——两条对称轴、两条渐近线;“两比率”——离心率、渐近线的斜率.双曲线的实轴长、虚轴长、焦距、离心率只与双曲线的形状和大小有关,而与双曲线的位置无关.双曲线的实轴端点坐标、虚轴端点坐标、焦点坐标、渐近线方程不仅与双曲线的形状和大小有关,而且与双曲线的实轴位置有关.
1.求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程.
利用双曲线的几何性质求其标准方程
巧设双曲线方程的六种方法与技巧
(5)渐近线为y=kx(k≠0)的双曲线方程可设为 .
(6)渐近线为ax±by=0的双曲线方程可设为 .
k2x2-y2=λ(λ≠0)
a2x2-b2y2=λ(λ≠0)
根据双曲线的某些几何性质求双曲线的方程,一般用待定系数法转化为解方程(组),但要注意焦点的位置,从而正确选择方程的形式.利用待定系数法求双曲线标准方程的关键是设出双曲线方程的标准形式,根据已知条件,列出关于a,b,c的方程并求出a,b,c的值.
(3)利用方程求.若得到的是关于a,c的齐次方程,即p·c2+q·ac+r·a2=0(p,q,r为常数,且p≠0),则转化为关于e的方程 求解.
p·e2+q·e+r=0
2.求双曲线离心率的取值范围,通常构造不等式求得,特别注意双曲线离心率 .
e∈(1,+∞)
双曲线离心率的值或取值范围的求法
1.知识清单:(1)根据双曲线的方程研究其几何性质.
(2)利用双曲线的几何性质求其标准方程.
(3)求双曲线离心率的值或取值范围.
2.方法归纳:定义法、待定系数法、转化与化归.
3.常见误区:(1)忽略双曲线焦点位置.
(2)求双曲线或离心率时漏解.
(3)忽略双曲线离心率范围(1,+∞).
课时作业 巩固提升
