24.4弧长和扇形面积 同步练习 2023-2024学年九年级数学上学期人教版(无答案)
文档属性
| 名称 | 24.4弧长和扇形面积 同步练习 2023-2024学年九年级数学上学期人教版(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 345.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 00:00:00 | ||
图片预览

文档简介
24.4弧长和扇形面积
同步练习
一、单选题
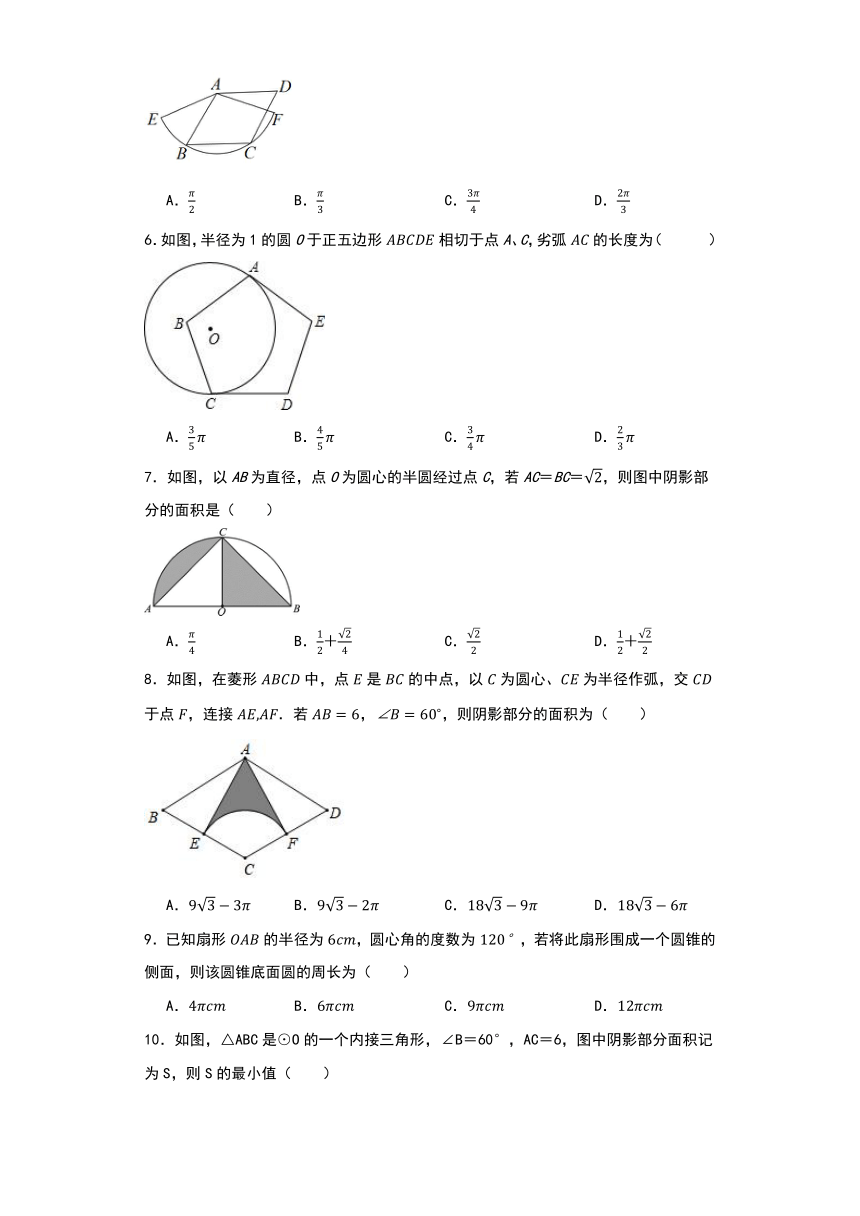
1.如图,阴影部分是两个半径为1的扇形,若α=120°,β=60°,则大扇形与小扇形的面积之差为( )
A. B. C. D.
2.一个含角的三角尺与一张圆形硬纸片如图放置在桌面上,圆心在斜边上,三角尺的两直角边与圆相切,切点分别为、.若,则阴影部分的面积为( )
A. B. C. D.
3.如图,在Rt△ABC中,,,,将绕点B顺时针旋转90°得到.在此旋转过程中所扫过的面积为( )
A.25π+24 B.5π+24 C.25π D.5π
4.圆心角是120°,半径为3的扇形面积为( )
A.π B.2π C.3π D.4π
5.如图,边长为2的菱形绕点旋转,当两点恰好落在扇形的上时,的长度等于( )
A. B. C. D.
6.如图,半径为1的圆O于正五边形相切于点A、C,劣弧的长度为( )
A. B. C. D.
7.如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC=,则图中阴影部分的面积是( )
A. B.+ C. D.+
8.如图,在菱形中,点是的中点,以为圆心、为半径作弧,交于点,连接.若,,则阴影部分的面积为( )
A. B. C. D.
9.已知扇形的半径为,圆心角的度数为,若将此扇形围成一个圆锥的侧面,则该圆锥底面圆的周长为( )
A. B. C. D.
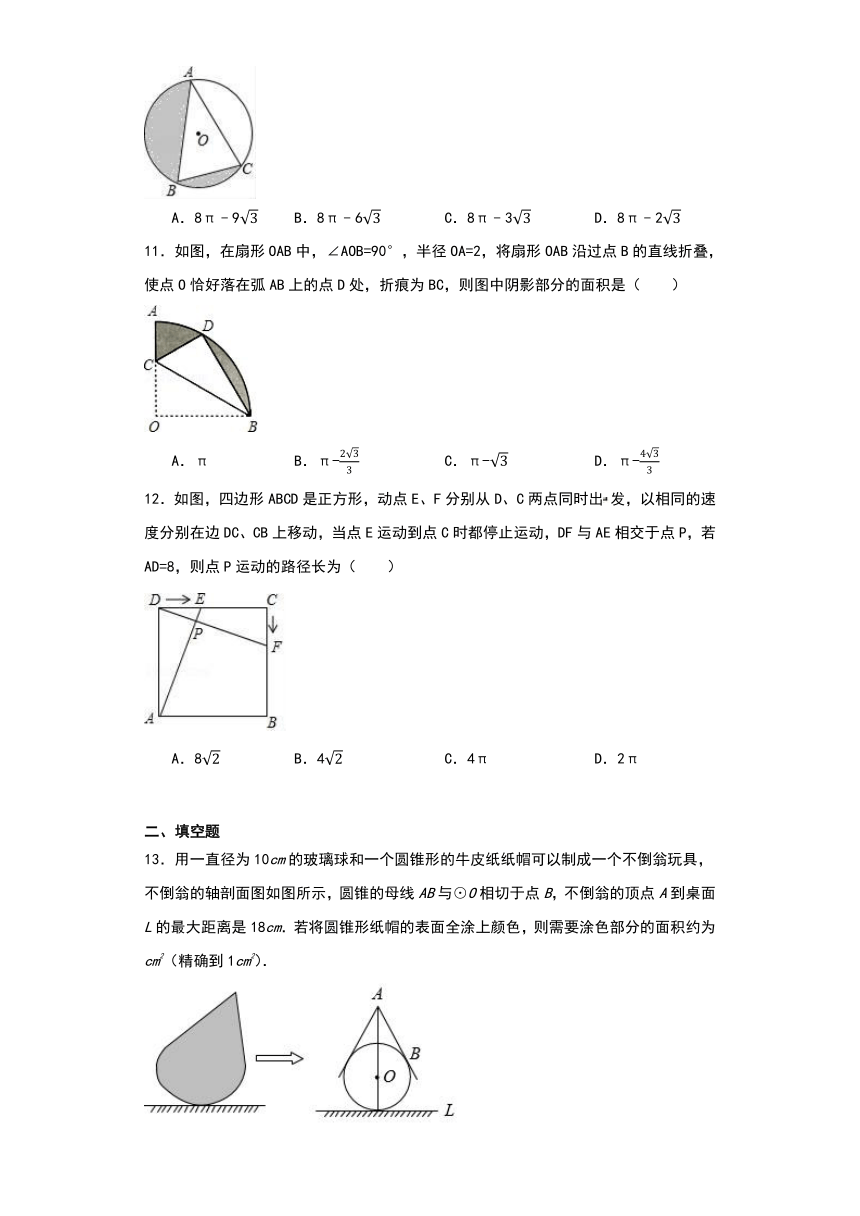
10.如图,△ABC是⊙O的一个内接三角形,∠B=60°,AC=6,图中阴影部分面积记为S,则S的最小值( )
A.8π﹣9 B.8π﹣6 C.8π﹣3 D.8π﹣2
11.如图,在扇形OAB中,∠AOB=90°,半径OA=2,将扇形OAB沿过点B的直线折叠,使点O恰好落在弧AB上的点D处,折痕为BC,则图中阴影部分的面积是( )
A.π B.π- C.π- D.π-
12.如图,四边形ABCD是正方形,动点E、F分别从D、C两点同时出发,以相同的速度分别在边DC、CB上移动,当点E运动到点C时都停止运动,DF与AE相交于点P,若AD=8,则点P运动的路径长为( )
A.8 B.4 C.4π D.2π
二、填空题
13.用一直径为10cm的玻璃球和一个圆锥形的牛皮纸纸帽可以制成一个不倒翁玩具,不倒翁的轴剖面图如图所示,圆锥的母线AB与⊙O相切于点B,不倒翁的顶点A到桌面L的最大距离是18cm.若将圆锥形纸帽的表面全涂上颜色,则需要涂色部分的面积约为 cm2(精确到1cm2).
14.如图,正方形ABCD的边长为1,分别以顶点A、B、C、D为圆心,1为半径画弧,四条弧交于点E、F、G、H,则图中阴影部分的外围周长为 .
15.已知扇形面积为24π,弧长为8π,则此扇形的圆心角为 度.
16.如图,AB是半圆的直径,弦CD∥AB,若AB=12 cm,∠CBD=30°,则阴影部分的图形面积是 cm2.(结果保留π)
17.一张圆形纸片裁剪后正好能做三个一样的无底圆锥纸帽(无余料,接缝不计),若圆锥的高为4cm,则每个圆锥的侧面积是 .
三、解答题
18.如图,是的直径,C是上一点,P是的延长线上一点,且.
(1)判断直线与的位置关系,并说明理由;
(2)若的半径为3,,求图中阴影部分的面积.
19.如图1,四边形内接于,为直径,过点作于点,连接.
(1)求证:;
(2)若是的切线,,连接,如图2.
①请判断四边形的形状,并说明理由;
②当时,求,与围成阴影部分的面积.
20.如图,A,B,C是⊙O上的点,其中,过点B画BD⊥OC于点D.
(1)求证:AB=2BD.
(2)若AB=,CD=2,求的长和图中涂色部分的面积.
21.如图,在平面直角坐标系中,的三个顶点坐标为,,.(每个方格的边长均为1个单位长度)
(1)请画出,使与关于原点对称;
(2)将绕点逆时针旋转90°,画出旋转后得到的,并直接写出线段旋转到扫过图形的面积.
22.如图△ABC中,AB=AC,AE⊥BC,E为垂足,F为AB上一点.以BF为直径的圆与AE相切于M点,交BC于G点.
(1)求证:BM平分∠ABC;
(2)当BC=2,时,
①求⊙O的半径;
②求图中阴影部分的面积.(结果保留π与根号)
23.如图,在平面直角坐标系中,三个顶点都在格点上,点,,的坐标分别为,,请解答下列问题:
(1)与△关于原点成中心对称,画出△并直接写出点的对应点的坐标;
(2)画出绕点顺时针旋转后得到的△,并求出线段旋转时扫过的面积.
24.如图1,已知⊙O与△ABC的边BC、AC分别相切于点D、E,BO是∠ABC的平分线,与⊙O相交于点G.
(1)求证:直线AB是⊙O的切线;
(2)已知⊙O的半径为2,如图2,点F是AB与⊙O的切点,连接OF、FG、DG,若OFDG.
①求证:四边形OFGD是菱形;
②求阴影部分的面积.
25.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=2.
(1)求AC的长度;
(2)求图中阴影部分的面积.(计算结果保留根号)
同步练习
一、单选题
1.如图,阴影部分是两个半径为1的扇形,若α=120°,β=60°,则大扇形与小扇形的面积之差为( )
A. B. C. D.
2.一个含角的三角尺与一张圆形硬纸片如图放置在桌面上,圆心在斜边上,三角尺的两直角边与圆相切,切点分别为、.若,则阴影部分的面积为( )
A. B. C. D.
3.如图,在Rt△ABC中,,,,将绕点B顺时针旋转90°得到.在此旋转过程中所扫过的面积为( )
A.25π+24 B.5π+24 C.25π D.5π
4.圆心角是120°,半径为3的扇形面积为( )
A.π B.2π C.3π D.4π
5.如图,边长为2的菱形绕点旋转,当两点恰好落在扇形的上时,的长度等于( )
A. B. C. D.
6.如图,半径为1的圆O于正五边形相切于点A、C,劣弧的长度为( )
A. B. C. D.
7.如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC=,则图中阴影部分的面积是( )
A. B.+ C. D.+
8.如图,在菱形中,点是的中点,以为圆心、为半径作弧,交于点,连接.若,,则阴影部分的面积为( )
A. B. C. D.
9.已知扇形的半径为,圆心角的度数为,若将此扇形围成一个圆锥的侧面,则该圆锥底面圆的周长为( )
A. B. C. D.
10.如图,△ABC是⊙O的一个内接三角形,∠B=60°,AC=6,图中阴影部分面积记为S,则S的最小值( )
A.8π﹣9 B.8π﹣6 C.8π﹣3 D.8π﹣2
11.如图,在扇形OAB中,∠AOB=90°,半径OA=2,将扇形OAB沿过点B的直线折叠,使点O恰好落在弧AB上的点D处,折痕为BC,则图中阴影部分的面积是( )
A.π B.π- C.π- D.π-
12.如图,四边形ABCD是正方形,动点E、F分别从D、C两点同时出发,以相同的速度分别在边DC、CB上移动,当点E运动到点C时都停止运动,DF与AE相交于点P,若AD=8,则点P运动的路径长为( )
A.8 B.4 C.4π D.2π
二、填空题
13.用一直径为10cm的玻璃球和一个圆锥形的牛皮纸纸帽可以制成一个不倒翁玩具,不倒翁的轴剖面图如图所示,圆锥的母线AB与⊙O相切于点B,不倒翁的顶点A到桌面L的最大距离是18cm.若将圆锥形纸帽的表面全涂上颜色,则需要涂色部分的面积约为 cm2(精确到1cm2).
14.如图,正方形ABCD的边长为1,分别以顶点A、B、C、D为圆心,1为半径画弧,四条弧交于点E、F、G、H,则图中阴影部分的外围周长为 .
15.已知扇形面积为24π,弧长为8π,则此扇形的圆心角为 度.
16.如图,AB是半圆的直径,弦CD∥AB,若AB=12 cm,∠CBD=30°,则阴影部分的图形面积是 cm2.(结果保留π)
17.一张圆形纸片裁剪后正好能做三个一样的无底圆锥纸帽(无余料,接缝不计),若圆锥的高为4cm,则每个圆锥的侧面积是 .
三、解答题
18.如图,是的直径,C是上一点,P是的延长线上一点,且.
(1)判断直线与的位置关系,并说明理由;
(2)若的半径为3,,求图中阴影部分的面积.
19.如图1,四边形内接于,为直径,过点作于点,连接.
(1)求证:;
(2)若是的切线,,连接,如图2.
①请判断四边形的形状,并说明理由;
②当时,求,与围成阴影部分的面积.
20.如图,A,B,C是⊙O上的点,其中,过点B画BD⊥OC于点D.
(1)求证:AB=2BD.
(2)若AB=,CD=2,求的长和图中涂色部分的面积.
21.如图,在平面直角坐标系中,的三个顶点坐标为,,.(每个方格的边长均为1个单位长度)
(1)请画出,使与关于原点对称;
(2)将绕点逆时针旋转90°,画出旋转后得到的,并直接写出线段旋转到扫过图形的面积.
22.如图△ABC中,AB=AC,AE⊥BC,E为垂足,F为AB上一点.以BF为直径的圆与AE相切于M点,交BC于G点.
(1)求证:BM平分∠ABC;
(2)当BC=2,时,
①求⊙O的半径;
②求图中阴影部分的面积.(结果保留π与根号)
23.如图,在平面直角坐标系中,三个顶点都在格点上,点,,的坐标分别为,,请解答下列问题:
(1)与△关于原点成中心对称,画出△并直接写出点的对应点的坐标;
(2)画出绕点顺时针旋转后得到的△,并求出线段旋转时扫过的面积.
24.如图1,已知⊙O与△ABC的边BC、AC分别相切于点D、E,BO是∠ABC的平分线,与⊙O相交于点G.
(1)求证:直线AB是⊙O的切线;
(2)已知⊙O的半径为2,如图2,点F是AB与⊙O的切点,连接OF、FG、DG,若OFDG.
①求证:四边形OFGD是菱形;
②求阴影部分的面积.
25.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=2.
(1)求AC的长度;
(2)求图中阴影部分的面积.(计算结果保留根号)
同课章节目录
