2023-2024学年九年级数学上学期人教版 24.3正多边形和圆 同步练习 (无答案)
文档属性
| 名称 | 2023-2024学年九年级数学上学期人教版 24.3正多边形和圆 同步练习 (无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 258.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 00:00:00 | ||
图片预览

文档简介
24.3正多边形和圆
同步练习
一、单选题
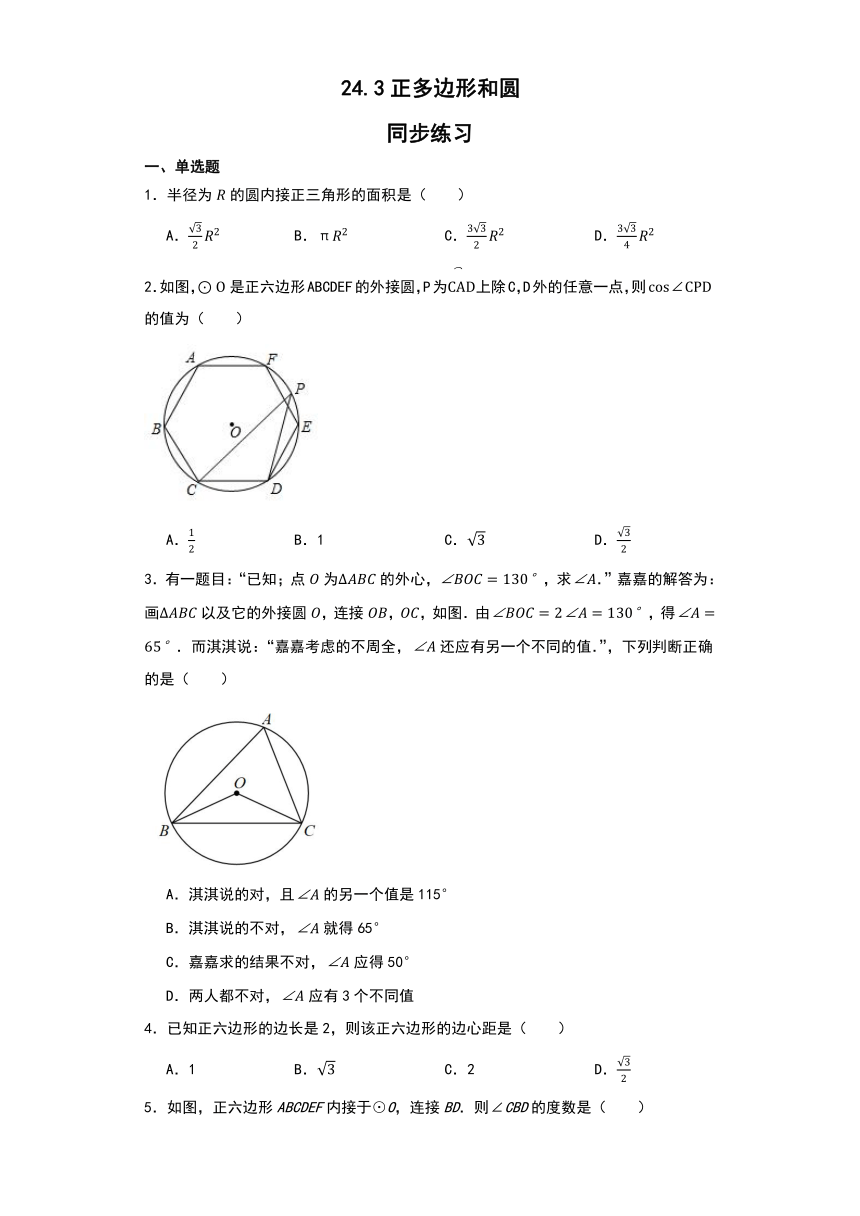
1.半径为的圆内接正三角形的面积是( )
A. B. C. D.
2.如图,是正六边形ABCDEF的外接圆,P为上除C,D外的任意一点,则的值为( )
A. B.1 C. D.
3.有一题目:“已知;点为的外心,,求.”嘉嘉的解答为:画以及它的外接圆,连接,,如图.由,得.而淇淇说:“嘉嘉考虑的不周全,还应有另一个不同的值.”,下列判断正确的是( )
A.淇淇说的对,且的另一个值是115°
B.淇淇说的不对,就得65°
C.嘉嘉求的结果不对,应得50°
D.两人都不对,应有3个不同值
4.已知正六边形的边长是2,则该正六边形的边心距是( )
A.1 B. C.2 D.
5.如图,正六边形ABCDEF内接于⊙O,连接BD.则∠CBD的度数是( )
A.30° B.45° C.60° D.90°
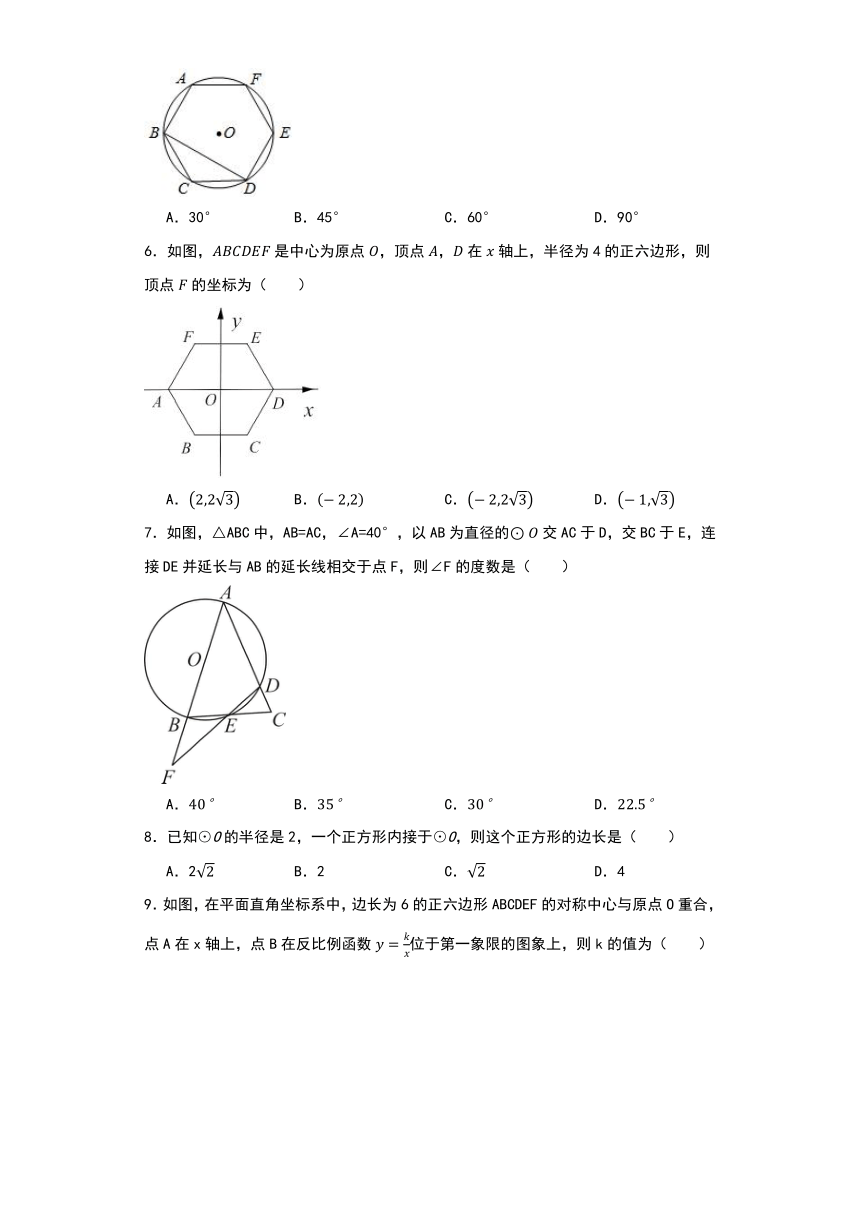
6.如图,是中心为原点,顶点,在轴上,半径为4的正六边形,则顶点的坐标为( )
A. B. C. D.
7.如图,△ABC中,AB=AC,∠A=40°,以AB为直径的交AC于D,交BC于E,连接DE并延长与AB的延长线相交于点F,则∠F的度数是( )
A. B. C. D.
8.已知⊙O的半径是2,一个正方形内接于⊙O,则这个正方形的边长是( )
A.2 B.2 C. D.4
9.如图,在平面直角坐标系中,边长为6的正六边形ABCDEF的对称中心与原点O重合,点A在x轴上,点B在反比例函数位于第一象限的图象上,则k的值为( )
A. B. C. D.
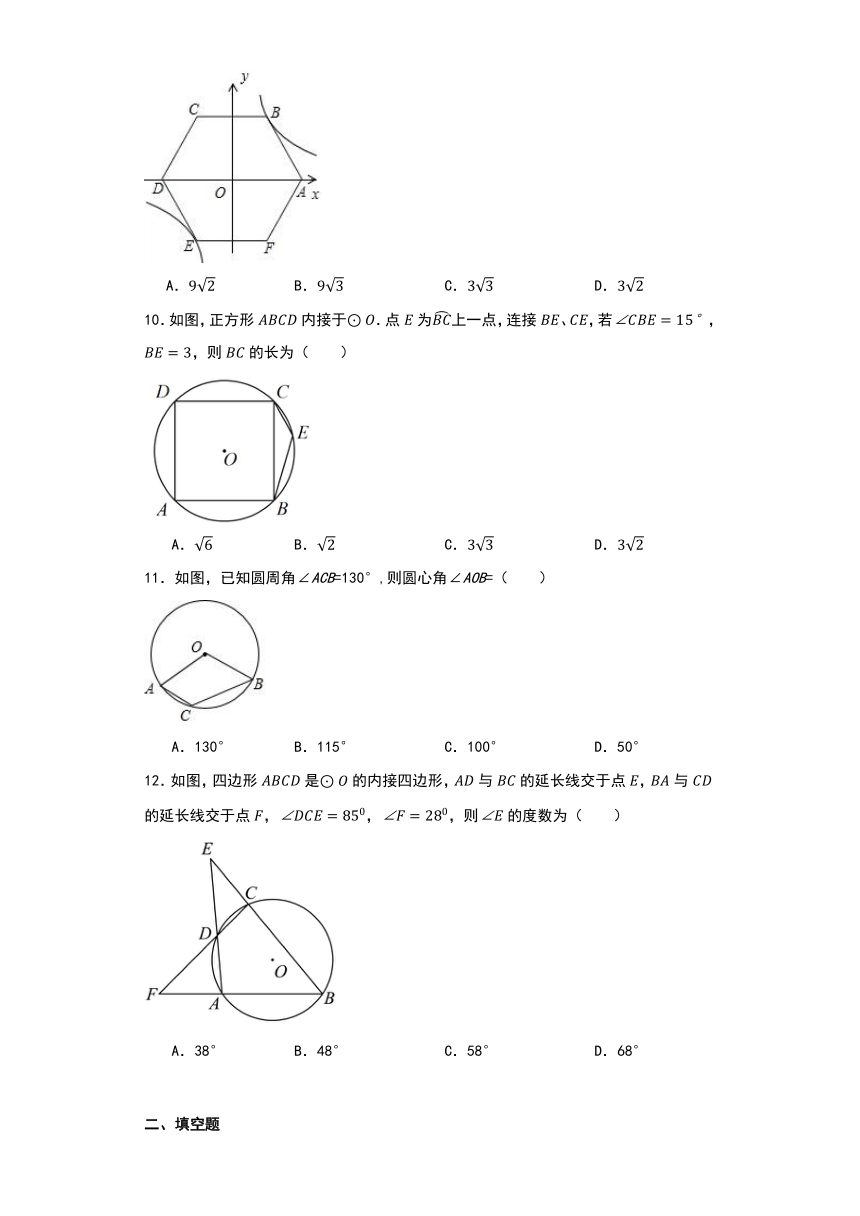
10.如图,正方形内接于.点为上一点,连接、,若,,则的长为( )
A. B. C. D.
11.如图,已知圆周角∠ACB=130°,则圆心角∠AOB=( )
A.130° B.115° C.100° D.50°
12.如图,四边形是的内接四边形,与的延长线交于点,与的延长线交于点,,,则的度数为( )
A.38° B.48° C.58° D.68°
二、填空题
13.线段AB是圆内接正十二边形的一条边,则AB边所对的圆周角是 °.
14.已知,的弦与的半径相等,则弦所对的圆周角的度数为 .
15.如图,已知正六边形ABCDEF内接于半径为4的⊙O,则阴影部分的面积为 .
16.如图,⊙O的半径为2,正八边形ABCDEFGH内接于⊙O,对角线CE、DF相交于点M,则△MEF的面积是 .
17.如图,正六边形硬纸片ABCDEF在桌面上由图1的起始位置沿直线l不滑行地翻滚一周后到图2位置,若正六边形的边长为2cm,则正六边形的中心O运动的路程为 cm.
三、解答题
18.如图,正六边形ABCDEF中,点M在AB边上,∠FMH=120°,MH与六边形外角的平分线BQ交于点H.
(1)当点M不与点A、B重合时,求证:∠AFM=∠BMH.
(2)当点M在正六边形ABCDEF一边AB上运动(点M不与点B重合)时,猜想FM与MH的数量关系,并对猜想的结果加以证明.
19.(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为弧BC上一动点,求证:PA=PB+PC.
下面给出一种证明方法,你可以按这一方法补全证明过程,也可以选择另外的证明方法.
证明:在AP上截取AE=CP,连接BE
∵△ABC是正三角形
∴AB=CB
∵∠1和∠2的同弧圆周角
∴∠1=∠2
∴△ABE≌△CBP
(2)如图2,四边形ABCD是⊙O的内接正方形,点P为弧BC上一动点,求证:PA=PC+ PB.
(3)如图3,六边形ABCDEF是⊙O的内接正六边形,点P为弧BC上一动点,请探究PA、PB、PC三者之间有何数量关系,直接写出结论.
20.一个正多边形的周长为60,边长为a,一个外角为b°.
(1)若a=6,求b的值;
(2)若b=30,求a的值.
21.如图正六边形ABCDEF.请分别在图1,图2中使用无刻度的直尺按要求画图.
(1)在图1中,画出一个与正六边形的边长相等的菱形;
(2)在图2中,画一个边长与正六边形的边长不相等的菱形.
22.(1)如图①,等边三角形△ABC内接于⊙O,AO的延长线交⊙O于点P,连接BP、CP.则AP、BP、CP之间的数量关系为:AP BP+CP.(填“>”、 “<” 或“=”)
(2)如图②,等边三角形△ABC内接于⊙O,点P是劣弧BC上任意一点,连接BP、CP.请探究AP、BP、CP之间的数量关系,并说明理由.
(3)如图③,正方形ABCD内接于⊙O,点P是劣弧BC上任意一点,连接AP、BP、CP.请直接写出AP、BP、CP之间的数量关系.
23.(1)已知:如图1,在矩形ABCD中,点E,F分别在AB,CD边上,BE=DF,连接CE,AF.求证:AF=CE.
(2)如图2,AB切⊙O于点B,OA=2,∠OAB=30°,弦BC∥OA.求:劣弧BC的长.(结果保留π)
24.每个小正方形都是边长为1个单位长度的小正方形,菱形OABC在平面直角坐标系中的位置如图所示.
(1)画出菱形OABC关于原点O的中心对称图形OA1B1C1,并直接写出点B1的坐标;
(2)将菱形OABO绕原点O顺时针旋转90°,得到菱形OA2B2C2,请画出菱形OA2B2C2并求出点B旋转到B2的路径长.
25.用钢丝制作两个不同的轴对称模型,如下图,这两个模型中大圆半径都是1米,模型甲中大圆内连接两个等边三角形,模型乙中大中圆内连接两个正方形.这两个图案哪个用料多一点?为什么?
同步练习
一、单选题
1.半径为的圆内接正三角形的面积是( )
A. B. C. D.
2.如图,是正六边形ABCDEF的外接圆,P为上除C,D外的任意一点,则的值为( )
A. B.1 C. D.
3.有一题目:“已知;点为的外心,,求.”嘉嘉的解答为:画以及它的外接圆,连接,,如图.由,得.而淇淇说:“嘉嘉考虑的不周全,还应有另一个不同的值.”,下列判断正确的是( )
A.淇淇说的对,且的另一个值是115°
B.淇淇说的不对,就得65°
C.嘉嘉求的结果不对,应得50°
D.两人都不对,应有3个不同值
4.已知正六边形的边长是2,则该正六边形的边心距是( )
A.1 B. C.2 D.
5.如图,正六边形ABCDEF内接于⊙O,连接BD.则∠CBD的度数是( )
A.30° B.45° C.60° D.90°
6.如图,是中心为原点,顶点,在轴上,半径为4的正六边形,则顶点的坐标为( )
A. B. C. D.
7.如图,△ABC中,AB=AC,∠A=40°,以AB为直径的交AC于D,交BC于E,连接DE并延长与AB的延长线相交于点F,则∠F的度数是( )
A. B. C. D.
8.已知⊙O的半径是2,一个正方形内接于⊙O,则这个正方形的边长是( )
A.2 B.2 C. D.4
9.如图,在平面直角坐标系中,边长为6的正六边形ABCDEF的对称中心与原点O重合,点A在x轴上,点B在反比例函数位于第一象限的图象上,则k的值为( )
A. B. C. D.
10.如图,正方形内接于.点为上一点,连接、,若,,则的长为( )
A. B. C. D.
11.如图,已知圆周角∠ACB=130°,则圆心角∠AOB=( )
A.130° B.115° C.100° D.50°
12.如图,四边形是的内接四边形,与的延长线交于点,与的延长线交于点,,,则的度数为( )
A.38° B.48° C.58° D.68°
二、填空题
13.线段AB是圆内接正十二边形的一条边,则AB边所对的圆周角是 °.
14.已知,的弦与的半径相等,则弦所对的圆周角的度数为 .
15.如图,已知正六边形ABCDEF内接于半径为4的⊙O,则阴影部分的面积为 .
16.如图,⊙O的半径为2,正八边形ABCDEFGH内接于⊙O,对角线CE、DF相交于点M,则△MEF的面积是 .
17.如图,正六边形硬纸片ABCDEF在桌面上由图1的起始位置沿直线l不滑行地翻滚一周后到图2位置,若正六边形的边长为2cm,则正六边形的中心O运动的路程为 cm.
三、解答题
18.如图,正六边形ABCDEF中,点M在AB边上,∠FMH=120°,MH与六边形外角的平分线BQ交于点H.
(1)当点M不与点A、B重合时,求证:∠AFM=∠BMH.
(2)当点M在正六边形ABCDEF一边AB上运动(点M不与点B重合)时,猜想FM与MH的数量关系,并对猜想的结果加以证明.
19.(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为弧BC上一动点,求证:PA=PB+PC.
下面给出一种证明方法,你可以按这一方法补全证明过程,也可以选择另外的证明方法.
证明:在AP上截取AE=CP,连接BE
∵△ABC是正三角形
∴AB=CB
∵∠1和∠2的同弧圆周角
∴∠1=∠2
∴△ABE≌△CBP
(2)如图2,四边形ABCD是⊙O的内接正方形,点P为弧BC上一动点,求证:PA=PC+ PB.
(3)如图3,六边形ABCDEF是⊙O的内接正六边形,点P为弧BC上一动点,请探究PA、PB、PC三者之间有何数量关系,直接写出结论.
20.一个正多边形的周长为60,边长为a,一个外角为b°.
(1)若a=6,求b的值;
(2)若b=30,求a的值.
21.如图正六边形ABCDEF.请分别在图1,图2中使用无刻度的直尺按要求画图.
(1)在图1中,画出一个与正六边形的边长相等的菱形;
(2)在图2中,画一个边长与正六边形的边长不相等的菱形.
22.(1)如图①,等边三角形△ABC内接于⊙O,AO的延长线交⊙O于点P,连接BP、CP.则AP、BP、CP之间的数量关系为:AP BP+CP.(填“>”、 “<” 或“=”)
(2)如图②,等边三角形△ABC内接于⊙O,点P是劣弧BC上任意一点,连接BP、CP.请探究AP、BP、CP之间的数量关系,并说明理由.
(3)如图③,正方形ABCD内接于⊙O,点P是劣弧BC上任意一点,连接AP、BP、CP.请直接写出AP、BP、CP之间的数量关系.
23.(1)已知:如图1,在矩形ABCD中,点E,F分别在AB,CD边上,BE=DF,连接CE,AF.求证:AF=CE.
(2)如图2,AB切⊙O于点B,OA=2,∠OAB=30°,弦BC∥OA.求:劣弧BC的长.(结果保留π)
24.每个小正方形都是边长为1个单位长度的小正方形,菱形OABC在平面直角坐标系中的位置如图所示.
(1)画出菱形OABC关于原点O的中心对称图形OA1B1C1,并直接写出点B1的坐标;
(2)将菱形OABO绕原点O顺时针旋转90°,得到菱形OA2B2C2,请画出菱形OA2B2C2并求出点B旋转到B2的路径长.
25.用钢丝制作两个不同的轴对称模型,如下图,这两个模型中大圆半径都是1米,模型甲中大圆内连接两个等边三角形,模型乙中大中圆内连接两个正方形.这两个图案哪个用料多一点?为什么?
同课章节目录
