8.1.1认识三角形[下学期]
图片预览





文档简介
课件22张PPT。9.1.1 认识三角形 三角形是一种基本的几何图形,生活中处处都有三角形的形象。
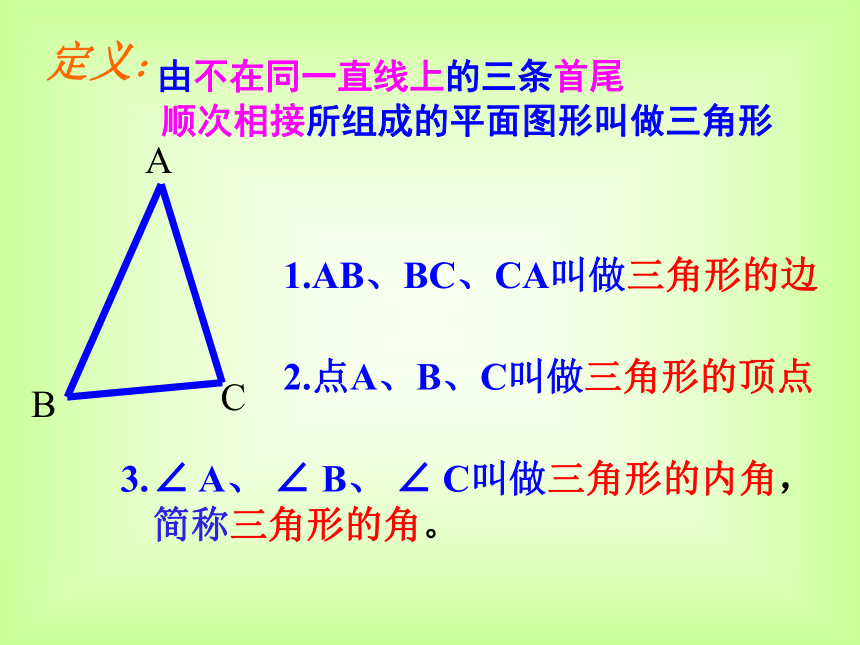
为什么在工程建筑、机械制造中经常采用三角形的结构呢?这与三角形的性质有关,虽然我们已对“三角形中三个角的和等于180度”等性质有了初步的了解,但还有必要对三角形的性质作进一步的探究。 由不在同一直线上的三条首尾 顺次相接所组成的平面图形叫做三角形ACB1.AB、BC、CA叫做三角形的边2.点A、B、C叫做三角形的顶点 ∠ A、 ∠ B、 ∠ C叫做三角形的内角,简称三角形的角。定义:ACB顶点是A 、B、C的三角形 记作:△ABCacb读作:三角形ABC三角形的边有时也用
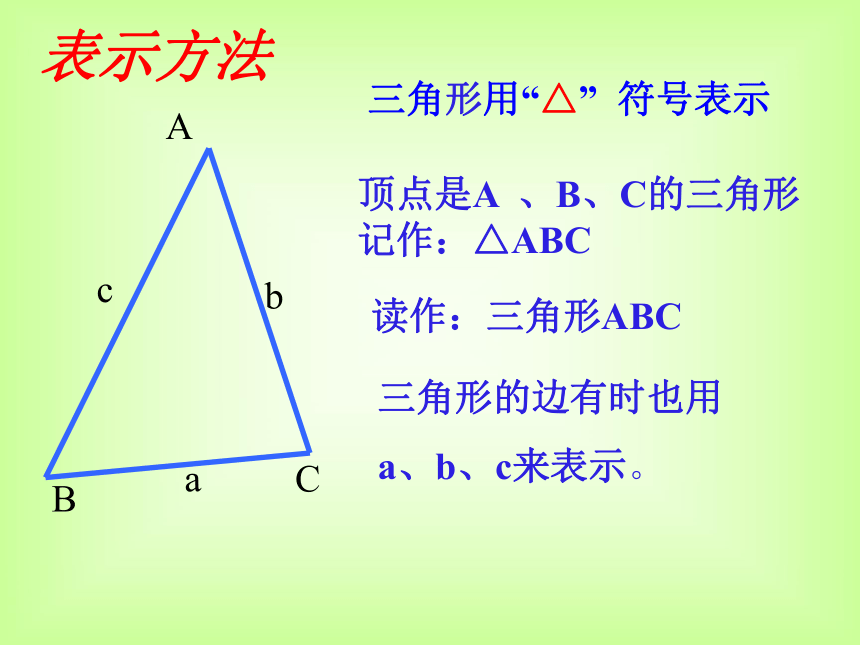
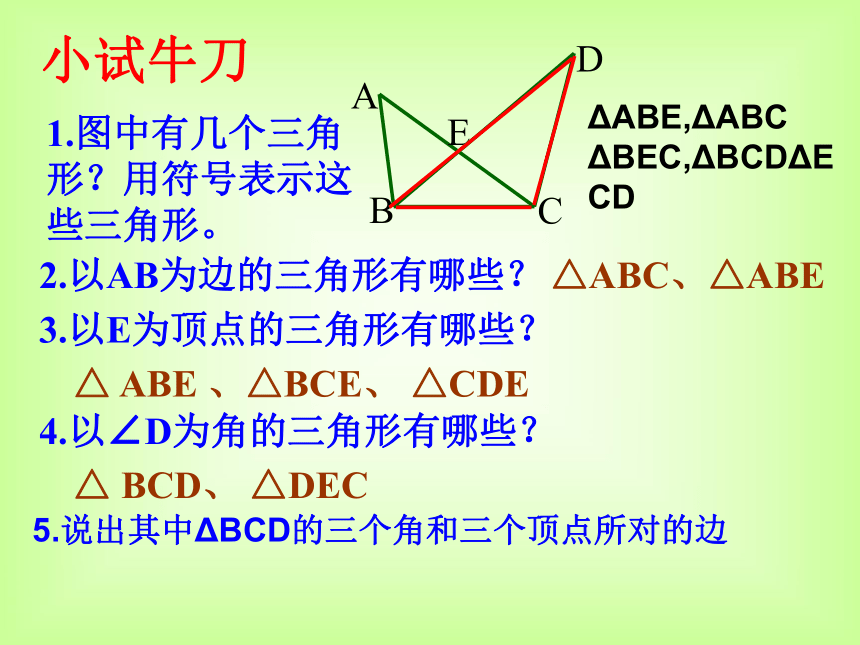
a、b、c来表示。三角形用“△” 符号表示表示方法1.图中有几个三角形?用符号表示这些三角形。2.以AB为边的三角形有哪些?△ABC、△ABE3.以E为顶点的三角形有哪些?△ ABE 、△BCE、 △CDE小试牛刀4.以∠D为角的三角形有哪些?△ BCD、 △DECΔABE,ΔABC
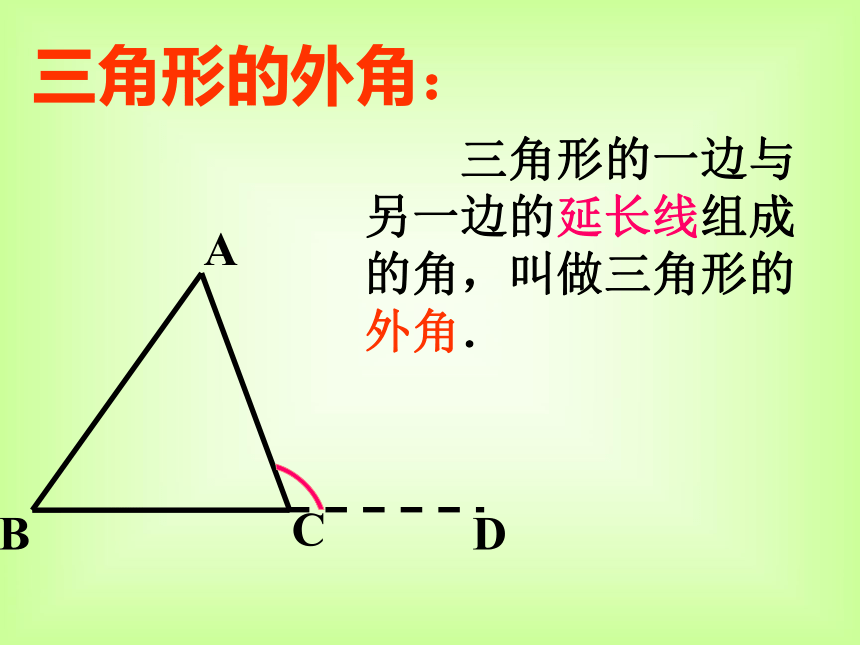
ΔBEC,ΔBCDΔECD5.说出其中ΔBCD的三个角和三个顶点所对的边D三角形的外角: 三角形的一边与另一边的延长线组成的角,叫做三角形的外角.按角分锐角三角形直角三角形钝角三角形不规则三角形等腰三角形三角形的分类只有两条边相等的等腰三角形等边三角形例1.画△ABC,在BC边上取三点D、E、F连接AD、
AE、AF.
(1)找出图形中所有三角形,用符号表示出来_______ (2) △ADE三边为______三内角为______
A B D E F C (3)∠ADB是______、______、______的外角。
(4) 以C为顶点的三角形有_______
(5)以AC为边的三角形
有_______
例2.三角形按角分为____________问:
(1)若△ABC中,∠A+ ∠ B= ∠ C,此三角形为______
(2)若△ABC中,一个内角大于相邻外角,此三角形为______
1.△ABC三边a,b,c,根据下列数据以边为标准说出各种三角形的形状.
(1)a=3,b=4,c=6;
(2) a=4,b=5,c=5;
(3)a:b:c=1:1:12.问:
若△ABC三角比为1;2:3,判断该三角形形状:
若△ABC三角比为1;2:6,判断该三角形形状:
若△ABC三角比为2;3:4,判断该三角形形状:
三角形的三个内角和是多少?把三个角拼在一起试试看?你有什么办法可以验证呢? 从刚才拼角的过程你能想出证明的办法吗?证法1:延长BC到CD,在△ABC的外部,以CA为一边,CE为另一边作∠1=∠A,
于是CE∥BA (内错角相等,两直线平行).
∴∠B=∠2 (两直线平行,同位角相等).
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°三角形的内角和等于1800.证法2:延长BC到D,过C作CE∥BA,
∴ ∠A=∠1 (两直线平行,内错角相等)
∠B=∠2 (两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°三角形的内角和等于1800.证法3:过A作EF∥BA,
∴∠B=∠2
(两直线平行,内错角相等)
∠C=∠1
(两直线平行,内错角相等)
又∵∠2+∠1+∠BAC=180°
∴∠B+∠C+∠BAC=180°三角形的内角和等于1800.证法4:过A作AE∥BC,
∴∠B=∠EAB (两直线平行,内错角相等)
∠EAC+∠C=180° (两直线平行,同旁内角互补) 即∠EAB+∠BAC+∠C =180°
∴∠B+∠BAC+∠C =180°三角形的内角和等于1800. 在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。思路总结 为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.(1)在△ABC中,∠A=35°,∠ B=43 °
则∠ C= .
(2)在△ABC中, ∠A :∠B:∠C=2:3:4
则∠A = ∠ B= ∠ C= . (1)一个三角形中最多有 个直角?为什么?
(2)一个三角形中最多有 个钝角?为什么?
(3)一个三角形中至少有 个锐角?为什么?
(4)任意一个三角形中,最大的一个角的度数至少为 .102 °80 °60 °40 °60°211新知应用讨论1、如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是 ( )(A)带①去 (B)带②去 (C)带③去 (D)带①和②去C练习再见
为什么在工程建筑、机械制造中经常采用三角形的结构呢?这与三角形的性质有关,虽然我们已对“三角形中三个角的和等于180度”等性质有了初步的了解,但还有必要对三角形的性质作进一步的探究。 由不在同一直线上的三条首尾 顺次相接所组成的平面图形叫做三角形ACB1.AB、BC、CA叫做三角形的边2.点A、B、C叫做三角形的顶点 ∠ A、 ∠ B、 ∠ C叫做三角形的内角,简称三角形的角。定义:ACB顶点是A 、B、C的三角形 记作:△ABCacb读作:三角形ABC三角形的边有时也用
a、b、c来表示。三角形用“△” 符号表示表示方法1.图中有几个三角形?用符号表示这些三角形。2.以AB为边的三角形有哪些?△ABC、△ABE3.以E为顶点的三角形有哪些?△ ABE 、△BCE、 △CDE小试牛刀4.以∠D为角的三角形有哪些?△ BCD、 △DECΔABE,ΔABC
ΔBEC,ΔBCDΔECD5.说出其中ΔBCD的三个角和三个顶点所对的边D三角形的外角: 三角形的一边与另一边的延长线组成的角,叫做三角形的外角.按角分锐角三角形直角三角形钝角三角形不规则三角形等腰三角形三角形的分类只有两条边相等的等腰三角形等边三角形例1.画△ABC,在BC边上取三点D、E、F连接AD、
AE、AF.
(1)找出图形中所有三角形,用符号表示出来_______ (2) △ADE三边为______三内角为______
A B D E F C (3)∠ADB是______、______、______的外角。
(4) 以C为顶点的三角形有_______
(5)以AC为边的三角形
有_______
例2.三角形按角分为____________问:
(1)若△ABC中,∠A+ ∠ B= ∠ C,此三角形为______
(2)若△ABC中,一个内角大于相邻外角,此三角形为______
1.△ABC三边a,b,c,根据下列数据以边为标准说出各种三角形的形状.
(1)a=3,b=4,c=6;
(2) a=4,b=5,c=5;
(3)a:b:c=1:1:12.问:
若△ABC三角比为1;2:3,判断该三角形形状:
若△ABC三角比为1;2:6,判断该三角形形状:
若△ABC三角比为2;3:4,判断该三角形形状:
三角形的三个内角和是多少?把三个角拼在一起试试看?你有什么办法可以验证呢? 从刚才拼角的过程你能想出证明的办法吗?证法1:延长BC到CD,在△ABC的外部,以CA为一边,CE为另一边作∠1=∠A,
于是CE∥BA (内错角相等,两直线平行).
∴∠B=∠2 (两直线平行,同位角相等).
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°三角形的内角和等于1800.证法2:延长BC到D,过C作CE∥BA,
∴ ∠A=∠1 (两直线平行,内错角相等)
∠B=∠2 (两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°三角形的内角和等于1800.证法3:过A作EF∥BA,
∴∠B=∠2
(两直线平行,内错角相等)
∠C=∠1
(两直线平行,内错角相等)
又∵∠2+∠1+∠BAC=180°
∴∠B+∠C+∠BAC=180°三角形的内角和等于1800.证法4:过A作AE∥BC,
∴∠B=∠EAB (两直线平行,内错角相等)
∠EAC+∠C=180° (两直线平行,同旁内角互补) 即∠EAB+∠BAC+∠C =180°
∴∠B+∠BAC+∠C =180°三角形的内角和等于1800. 在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。思路总结 为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.(1)在△ABC中,∠A=35°,∠ B=43 °
则∠ C= .
(2)在△ABC中, ∠A :∠B:∠C=2:3:4
则∠A = ∠ B= ∠ C= . (1)一个三角形中最多有 个直角?为什么?
(2)一个三角形中最多有 个钝角?为什么?
(3)一个三角形中至少有 个锐角?为什么?
(4)任意一个三角形中,最大的一个角的度数至少为 .102 °80 °60 °40 °60°211新知应用讨论1、如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是 ( )(A)带①去 (B)带②去 (C)带③去 (D)带①和②去C练习再见
