垂径定理[上学期]
图片预览

文档简介
垂直于弦的直径
教学目标:
1、利用圆的对称性,通过观察使学生能归纳出垂径定理的主要内容。
2、利用垂径定理的结论进行证明,并能通过构造直角三角形解决一些简单的计算问题。
教学重点:
能灵活运用垂径定理的结论进行证明,并能通过构造直角三角形解决一些简单的计算问题。
教学过程:
复习提问:
1.如果一个图形沿着一条直线对折,直线两旁的部分能够完全互相重合,那么这个图形叫做 轴对称图形,这条直线叫做它的对称轴
2. 等腰三角形是轴对称图形,它的对称轴是底边上的高所在的直线
3. 等边三角形是不是轴对称图形,它有几条对称轴?正方形呢?
新课讲授:
问题1:作⊙O的直径AB,然后沿着AB对折⊙O,会出现什么现象,说明了什么?
圆是轴对称图形,它的对称轴是任意一条过圆心的直线.
问题2:在⊙O上取一点C,作CD⊥AB,垂足为E,你能发现哪些结论?
垂径定理:垂直于弦的直径平分这条弦,
并且平分弦所对的两条弧.
∵在⊙O中,若AB是直径,CD是弦,AB⊥CD,垂足是E
∴CE=DE, AC = AD,CB = DB
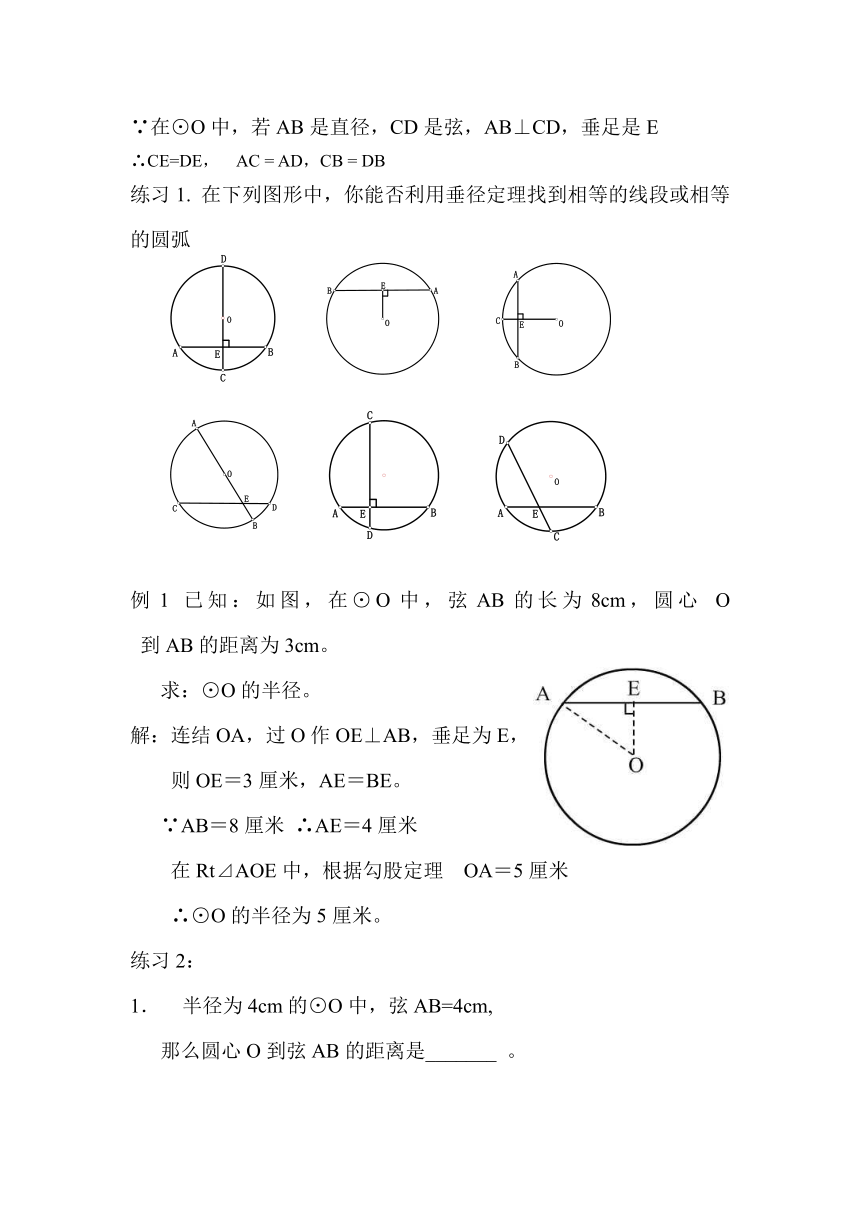
练习1. 在下列图形中,你能否利用垂径定理找到相等的线段或相等的圆弧
例1 已知:如图,在⊙O中,弦AB的长为8cm,圆心 O 到AB的距离为3cm。
求:⊙O的半径。
解:连结OA,过O作OE⊥AB,垂足为E,
则OE=3厘米,AE=BE。
∵AB=8厘米 ∴AE=4厘米
在Rt⊿AOE中,根据勾股定理 OA=5厘米
∴⊙O的半径为5厘米。
练习2:
1. 半径为4cm的⊙O中,弦AB=4cm,
那么圆心O到弦AB的距离是_______ 。
2.半径为2cm的圆中,过半径中点且
垂直于这条半径的弦长是______ 。
3.在⊙O中,弦AB=12厘米,OC⊥AB,CD=2cm
则⊙O的半径为_______ 。
1 2 3
5. 过⊙O内一点M的最长的弦为4,最短的弦为2,则OM的长为 .
例2 已知:在以O为圆心的两个同心圆中,大圆的直径AB交小圆于C、D两点
(1)若AB为直径
求证: AC = BD
(2)若AB为不过圆心的弦
猜想AC 与 BD的大小关系,并证明。
(3)若AB=8,CD=4,求圆环的面积.
思考:
例3 已知:在以圆O为圆心的两个同心圆中,大圆的弦AB交小圆于F、G两点,PQ是小圆的直径,PC⊥AB于C, QD⊥AB于D
求证:AC = BD
课堂小结
请大家围绕以下两个问题小结本节课
① 学习了一个与圆有关的重要定理,定
理的内容是什么?
② 在圆中解决与弦有关问题时经常
作的辅助线是什么?
1.垂径定理相当于说一条直线如果具备(1)过圆心;(2)垂直于弦;则它有以下性质(3)平分弦;(4)平分弦所对的劣弧;(5)平分弦所对的优弧。
2.在圆中解决有关于弦的问题时,经常是过圆心作弦的垂线段,连结半径等辅助线,构造直角三角形。为应用垂径定理创造条件。
教学目标:
1、利用圆的对称性,通过观察使学生能归纳出垂径定理的主要内容。
2、利用垂径定理的结论进行证明,并能通过构造直角三角形解决一些简单的计算问题。
教学重点:
能灵活运用垂径定理的结论进行证明,并能通过构造直角三角形解决一些简单的计算问题。
教学过程:
复习提问:
1.如果一个图形沿着一条直线对折,直线两旁的部分能够完全互相重合,那么这个图形叫做 轴对称图形,这条直线叫做它的对称轴
2. 等腰三角形是轴对称图形,它的对称轴是底边上的高所在的直线
3. 等边三角形是不是轴对称图形,它有几条对称轴?正方形呢?
新课讲授:
问题1:作⊙O的直径AB,然后沿着AB对折⊙O,会出现什么现象,说明了什么?
圆是轴对称图形,它的对称轴是任意一条过圆心的直线.
问题2:在⊙O上取一点C,作CD⊥AB,垂足为E,你能发现哪些结论?
垂径定理:垂直于弦的直径平分这条弦,
并且平分弦所对的两条弧.
∵在⊙O中,若AB是直径,CD是弦,AB⊥CD,垂足是E
∴CE=DE, AC = AD,CB = DB
练习1. 在下列图形中,你能否利用垂径定理找到相等的线段或相等的圆弧
例1 已知:如图,在⊙O中,弦AB的长为8cm,圆心 O 到AB的距离为3cm。
求:⊙O的半径。
解:连结OA,过O作OE⊥AB,垂足为E,
则OE=3厘米,AE=BE。
∵AB=8厘米 ∴AE=4厘米
在Rt⊿AOE中,根据勾股定理 OA=5厘米
∴⊙O的半径为5厘米。
练习2:
1. 半径为4cm的⊙O中,弦AB=4cm,
那么圆心O到弦AB的距离是_______ 。
2.半径为2cm的圆中,过半径中点且
垂直于这条半径的弦长是______ 。
3.在⊙O中,弦AB=12厘米,OC⊥AB,CD=2cm
则⊙O的半径为_______ 。
1 2 3
5. 过⊙O内一点M的最长的弦为4,最短的弦为2,则OM的长为 .
例2 已知:在以O为圆心的两个同心圆中,大圆的直径AB交小圆于C、D两点
(1)若AB为直径
求证: AC = BD
(2)若AB为不过圆心的弦
猜想AC 与 BD的大小关系,并证明。
(3)若AB=8,CD=4,求圆环的面积.
思考:
例3 已知:在以圆O为圆心的两个同心圆中,大圆的弦AB交小圆于F、G两点,PQ是小圆的直径,PC⊥AB于C, QD⊥AB于D
求证:AC = BD
课堂小结
请大家围绕以下两个问题小结本节课
① 学习了一个与圆有关的重要定理,定
理的内容是什么?
② 在圆中解决与弦有关问题时经常
作的辅助线是什么?
1.垂径定理相当于说一条直线如果具备(1)过圆心;(2)垂直于弦;则它有以下性质(3)平分弦;(4)平分弦所对的劣弧;(5)平分弦所对的优弧。
2.在圆中解决有关于弦的问题时,经常是过圆心作弦的垂线段,连结半径等辅助线,构造直角三角形。为应用垂径定理创造条件。
