华师大版数学八年级上册 14.1.1 直角三角形三边的关系(2)教案
文档属性
| 名称 | 华师大版数学八年级上册 14.1.1 直角三角形三边的关系(2)教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 129.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 00:00:00 | ||
图片预览

文档简介
14.1.1 直角三角形三边的关系(2)
1.引导学生用拼图法、等积法验证勾股定理的正确性;
2.让学生学会使用勾股定理解决简单实际问题;
3.结合解题过程,培养学生数形结合的数学思想.
应用勾股定理时,注意正确使用定理和重视定理存在的条件.
利用勾股定理解决实际问题.
一、情景导入 感受新知
问题情境:1.勾股定理的内容是什么?
直角三角形两直角边的平方和等于斜边的平方.
2.填表:
Rt△ABC a b c
∠C=90° 6 8 10
∠C=90° 5 12 13
∠C=90° 2 4 6
∠A=90° 5 4 3
∠B=90° 5 13 12
二、自学互研 生成新知
【自主探究】
阅读教材P110~P112,完成下面的内容:
活动:验证定理
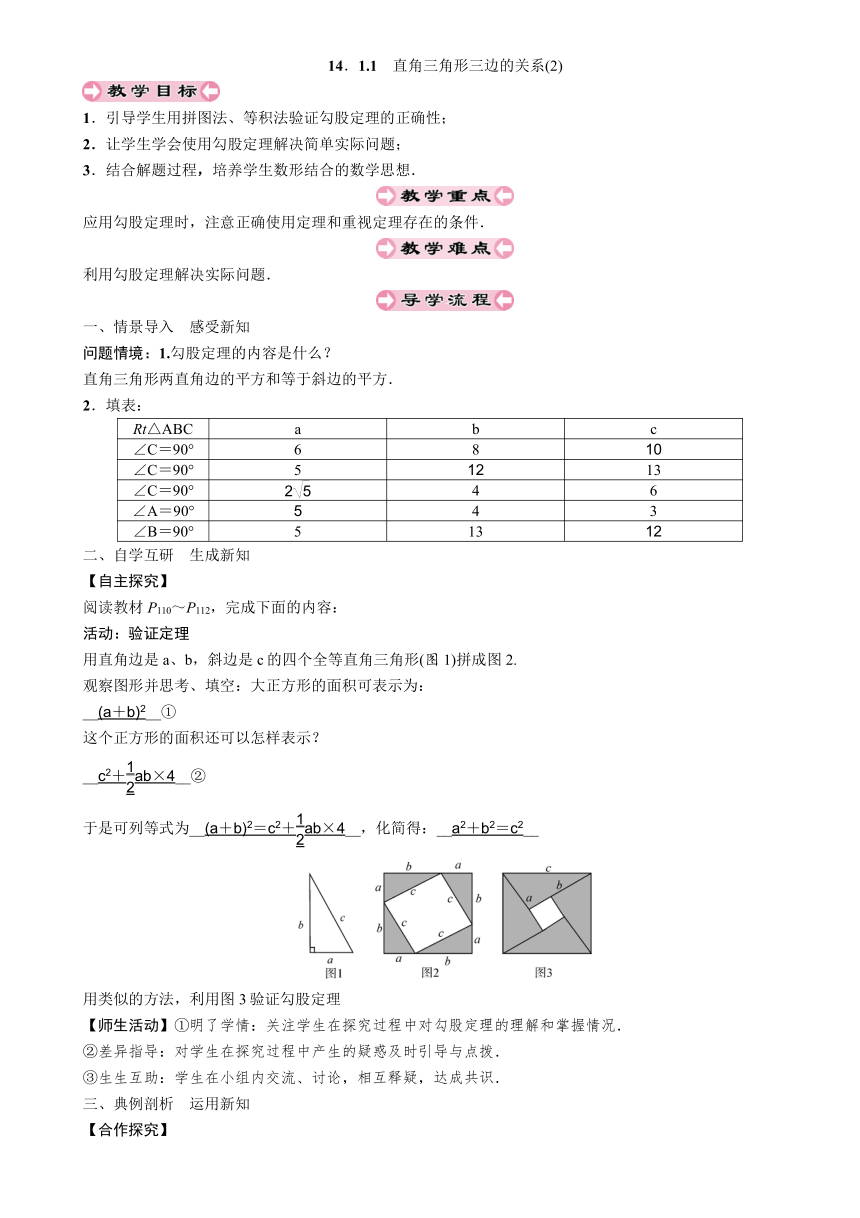
用直角边是a、b,斜边是c的四个全等直角三角形(图1)拼成图2.
观察图形并思考、填空:大正方形的面积可表示为:
__(a+b)2__①
这个正方形的面积还可以怎样表示?
__c2+ab×4__②
于是可列等式为__(a+b)2=c2+ab×4__,化简得:__a2+b2=c2__
用类似的方法,利用图3验证勾股定理
【师生活动】①明了学情:关注学生在探究过程中对勾股定理的理解和掌握情况.
②差异指导:对学生在探究过程中产生的疑惑及时引导与点拨.
③生生互助:学生在小组内交流、讨论,相互释疑,达成共识.
三、典例剖析 运用新知
【合作探究】
例1:如图,将长为6米的梯子AC斜靠在墙上,BC长为2米,求梯子上端A到墙的底端B的距离AB.(精确到0.01米)
解:AB===4(m).
例2:如图,为了求出湖两岸的A、B两点之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC长160米,BC长128米.问从点A穿过湖到点B有多远?
(注意引导学生把实际问题转化为数学模式.)
解:∵△ABC为直角三角形,
∴BA===96m.
四、课堂小结 回顾新知
通过今天的学习,你有了哪些新的收获?还存在哪些疑惑?如果你对勾股定理另有自己的想法和证法,请你告诉同学们.
五、检测反馈 落实新知
1.如图,字母B所代表的正方形的面积是(C)
A.12 B.13 C.144 D.194
,(第1题图)) ,(第4题图))
2.一直角三角形的两条边分别为12、5,则第三边的长为__13或__.
3.在△ABC中,AB=13cm,AC=15cm,BC边上的高AD=12,则BC的长为__14__.
4.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和是__49cm2__.
5.已知△ABC中,∠B=90°,AC=25cm, BC=15cm,求AB的长.
解:AB===20cm.
六、课后作业 巩固新知
见学生用书.
1.引导学生用拼图法、等积法验证勾股定理的正确性;
2.让学生学会使用勾股定理解决简单实际问题;
3.结合解题过程,培养学生数形结合的数学思想.
应用勾股定理时,注意正确使用定理和重视定理存在的条件.
利用勾股定理解决实际问题.
一、情景导入 感受新知
问题情境:1.勾股定理的内容是什么?
直角三角形两直角边的平方和等于斜边的平方.
2.填表:
Rt△ABC a b c
∠C=90° 6 8 10
∠C=90° 5 12 13
∠C=90° 2 4 6
∠A=90° 5 4 3
∠B=90° 5 13 12
二、自学互研 生成新知
【自主探究】
阅读教材P110~P112,完成下面的内容:
活动:验证定理
用直角边是a、b,斜边是c的四个全等直角三角形(图1)拼成图2.
观察图形并思考、填空:大正方形的面积可表示为:
__(a+b)2__①
这个正方形的面积还可以怎样表示?
__c2+ab×4__②
于是可列等式为__(a+b)2=c2+ab×4__,化简得:__a2+b2=c2__
用类似的方法,利用图3验证勾股定理
【师生活动】①明了学情:关注学生在探究过程中对勾股定理的理解和掌握情况.
②差异指导:对学生在探究过程中产生的疑惑及时引导与点拨.
③生生互助:学生在小组内交流、讨论,相互释疑,达成共识.
三、典例剖析 运用新知
【合作探究】
例1:如图,将长为6米的梯子AC斜靠在墙上,BC长为2米,求梯子上端A到墙的底端B的距离AB.(精确到0.01米)
解:AB===4(m).
例2:如图,为了求出湖两岸的A、B两点之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC长160米,BC长128米.问从点A穿过湖到点B有多远?
(注意引导学生把实际问题转化为数学模式.)
解:∵△ABC为直角三角形,
∴BA===96m.
四、课堂小结 回顾新知
通过今天的学习,你有了哪些新的收获?还存在哪些疑惑?如果你对勾股定理另有自己的想法和证法,请你告诉同学们.
五、检测反馈 落实新知
1.如图,字母B所代表的正方形的面积是(C)
A.12 B.13 C.144 D.194
,(第1题图)) ,(第4题图))
2.一直角三角形的两条边分别为12、5,则第三边的长为__13或__.
3.在△ABC中,AB=13cm,AC=15cm,BC边上的高AD=12,则BC的长为__14__.
4.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和是__49cm2__.
5.已知△ABC中,∠B=90°,AC=25cm, BC=15cm,求AB的长.
解:AB===20cm.
六、课后作业 巩固新知
见学生用书.
