人教版高中数学选择性必修第一册3.3.2 第一课时 抛物线的简单几何性质 课件(共35张PPT)
文档属性
| 名称 | 人教版高中数学选择性必修第一册3.3.2 第一课时 抛物线的简单几何性质 课件(共35张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 00:00:00 | ||
图片预览











文档简介
(共35张PPT)
3.3.2 抛物线的简单几何性质
第一课时 抛物线的简单几何性质
[学习目标]
1.了解抛物线的几何图形及简单几何性质.
2.能用抛物线的简单几何性质解决一些简单的问题.
必备知识 自主探究
关键能力 互动探究
课时作业 巩固提升
问题1 类比用方程研究椭圆、双曲线几何性质的过程与方法,你认为应该研究抛物线的哪些几何性质?
问题2 椭圆、双曲线、抛物线的离心率的范围如何?
D
2.准线方程为x=2的抛物线的标准方程为____________.
y2=-8x
3.对称轴为x轴,顶点与焦点距离等于6的抛物线的标准方程为______________.
y2=±24x
抛物线的几何性质
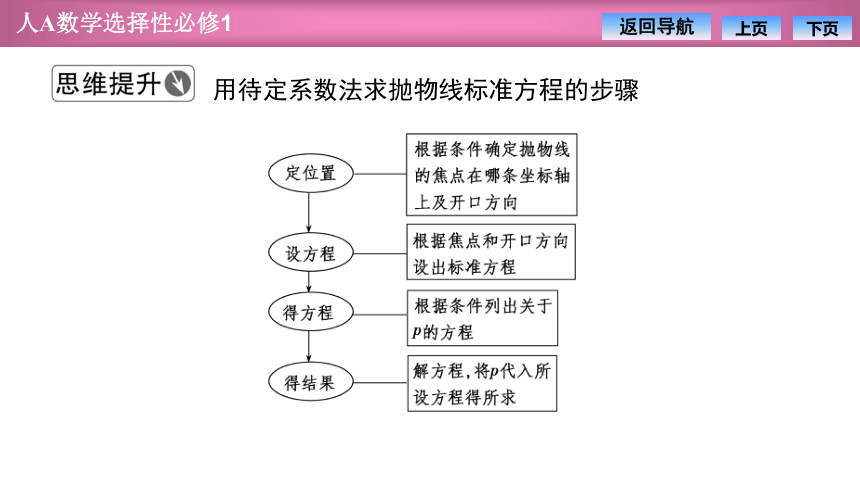
用待定系数法求抛物线标准方程的步骤
1.求适合下列条件的抛物线的标准方程,并写出焦点坐标与准线方程.
(1)焦点F关于准线的对称点为M(0,-9);
(2)关于y轴对称,与直线y=-12相交所得线段的长为12.
抛物线的焦点弦长
1.AB是过抛物线y2=2px(p>0)焦点的弦,设A(x1,y1),B(x2,y2),则|AB|= .
x1+x2+p
2p
2p
(2)通径是所有焦点弦中长度最 的弦.
短
[例2] 斜率为1的直线l经过抛物线y2=4x的焦点F,且与抛物线相交于A,B两点,求线段AB的长.
分析:法一:由抛物线的方程可以得到它的焦点坐标,又直线l的斜率为1,所以可以求出直线l的方程;与抛物线的方程联立,可以求出A,B两点的坐标;利用两点间的距离公式可以求出|AB|.这种方法思路直接,具有一般性.
因为直线l的斜率为1,且过焦点F(1,0),所以直线l的方程为y=x-1.①
将①代入方程y2=4x,得(x-1)2=4x,化简,得x2-6x+1=0.
所以x1+x2=6,
|AB|=x1+x2+2=8.
所以线段AB的长是8.
-p2
[例3] 经过抛物线焦点F的直线交抛物线于A,B两点,经过点A和抛物线顶点的直线交抛物线的准线于点D,求证:直线DB平行于抛物线的对称轴.
分析:我们用坐标法证明这个结论,即通过建立抛物线及直线的方程,运用方程研究直线DB与抛物线对称轴之间的位置关系.建立直角坐标系,只要证明点D的纵坐标与点B的纵坐标相等即可.
[证明] 如图,以抛物线的对称轴为x轴,抛物线的顶点为原点,建立平面直角坐标系Oxy.设抛物线的方程为y2=2px(p>0),①
1.过抛物线焦点F的直线与抛物线交于A,B两点,过B作抛物线对称轴的平行线交准线于D,则A,O,D三点共线.
2.过准线上任意一点D,连接DO交抛物线于A,过D作抛物线对称轴的平行线交抛物线于B,则A,F,B三点共线.
3.已知抛物线y2=2px(p>0)的焦点为F,过F的直线l与抛物线交于A,B两点,A,B在准线上的射影分别为A1,B1.
证明:A1F⊥B1F.
法二:如图所示,
由抛物线定义,知
|AF|=|AA1|,|BF|=|BB1|,
则∠AFA1=∠AA1F=∠A1FO=θ1,
∠BFB1=∠BB1F=∠B1FO=θ2.
1.知识清单:(1)抛物线的几何性质.
(2)抛物线的焦点弦长.
(3)抛物线的焦点弦性质.
2.方法归纳:图象法、待定系数法.
3.常见误区:忽略焦点的位置而致错.
课时作业 巩固提升
3.3.2 抛物线的简单几何性质
第一课时 抛物线的简单几何性质
[学习目标]
1.了解抛物线的几何图形及简单几何性质.
2.能用抛物线的简单几何性质解决一些简单的问题.
必备知识 自主探究
关键能力 互动探究
课时作业 巩固提升
问题1 类比用方程研究椭圆、双曲线几何性质的过程与方法,你认为应该研究抛物线的哪些几何性质?
问题2 椭圆、双曲线、抛物线的离心率的范围如何?
D
2.准线方程为x=2的抛物线的标准方程为____________.
y2=-8x
3.对称轴为x轴,顶点与焦点距离等于6的抛物线的标准方程为______________.
y2=±24x
抛物线的几何性质
用待定系数法求抛物线标准方程的步骤
1.求适合下列条件的抛物线的标准方程,并写出焦点坐标与准线方程.
(1)焦点F关于准线的对称点为M(0,-9);
(2)关于y轴对称,与直线y=-12相交所得线段的长为12.
抛物线的焦点弦长
1.AB是过抛物线y2=2px(p>0)焦点的弦,设A(x1,y1),B(x2,y2),则|AB|= .
x1+x2+p
2p
2p
(2)通径是所有焦点弦中长度最 的弦.
短
[例2] 斜率为1的直线l经过抛物线y2=4x的焦点F,且与抛物线相交于A,B两点,求线段AB的长.
分析:法一:由抛物线的方程可以得到它的焦点坐标,又直线l的斜率为1,所以可以求出直线l的方程;与抛物线的方程联立,可以求出A,B两点的坐标;利用两点间的距离公式可以求出|AB|.这种方法思路直接,具有一般性.
因为直线l的斜率为1,且过焦点F(1,0),所以直线l的方程为y=x-1.①
将①代入方程y2=4x,得(x-1)2=4x,化简,得x2-6x+1=0.
所以x1+x2=6,
|AB|=x1+x2+2=8.
所以线段AB的长是8.
-p2
[例3] 经过抛物线焦点F的直线交抛物线于A,B两点,经过点A和抛物线顶点的直线交抛物线的准线于点D,求证:直线DB平行于抛物线的对称轴.
分析:我们用坐标法证明这个结论,即通过建立抛物线及直线的方程,运用方程研究直线DB与抛物线对称轴之间的位置关系.建立直角坐标系,只要证明点D的纵坐标与点B的纵坐标相等即可.
[证明] 如图,以抛物线的对称轴为x轴,抛物线的顶点为原点,建立平面直角坐标系Oxy.设抛物线的方程为y2=2px(p>0),①
1.过抛物线焦点F的直线与抛物线交于A,B两点,过B作抛物线对称轴的平行线交准线于D,则A,O,D三点共线.
2.过准线上任意一点D,连接DO交抛物线于A,过D作抛物线对称轴的平行线交抛物线于B,则A,F,B三点共线.
3.已知抛物线y2=2px(p>0)的焦点为F,过F的直线l与抛物线交于A,B两点,A,B在准线上的射影分别为A1,B1.
证明:A1F⊥B1F.
法二:如图所示,
由抛物线定义,知
|AF|=|AA1|,|BF|=|BB1|,
则∠AFA1=∠AA1F=∠A1FO=θ1,
∠BFB1=∠BB1F=∠B1FO=θ2.
1.知识清单:(1)抛物线的几何性质.
(2)抛物线的焦点弦长.
(3)抛物线的焦点弦性质.
2.方法归纳:图象法、待定系数法.
3.常见误区:忽略焦点的位置而致错.
课时作业 巩固提升
