2023-2024学年人教版八年级数学上册13.1.1轴对称 课件(共22张PPT)
文档属性
| 名称 | 2023-2024学年人教版八年级数学上册13.1.1轴对称 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 556.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
第十三章 轴对称
轴对称
教学目标:
【知识与技能】
(1)理解轴对称图形和两个图形关于某条直线对称的概念.
(2)了解轴对称图形的对称轴,两个图形关于某条直线对称的对应点.
(3)掌握线段垂直平分线的概念.
(4)理解和掌握轴对称的性质.
【过程与方法】
通过已知图形画对称轴及画轴对称图形,让学生体会轴对称图形的性质和轴对称在实际生活中的应用.
【情感态度与价值观】
通过对轴对称图形和轴对称的认识,增强学生对对称美的认识,使学生感受数学带来的美.
教学重难点:
1轴对称图形和两个图形关于某条直线对称的概念.
2轴对称图形和两个图形关于某条直线对称的区别和联系.
1.(2022新课标)理解轴对称图形的概念.
2.(2022新课标)通过具体实例理解轴对称的概念,探索它的基本性质:成轴对称的两个图形中对应点的连线被对称轴垂直平分.
3.通过自己动手画、作、测量、计算和推理证明,体会轴对称的性质.
知识点一:轴对称图形
如果一个平面图形沿着一条直线折叠,直线两旁的部分能够 ,那么这个图形就叫做轴对称图形.
这条直线就是它的 .
对称轴
互相重合
A B C D
1.(跨学科融合)(2022青岛一模)2022年2月4日至20日,第24届冬奥会在北京和张家口举办,北京是唯一同时举办过夏季和冬季奥运会的城市.下列4个图形是四届冬奥会的部分图标,属于轴对称图形的是( )
C
知识点二:轴对称
把一个图形沿着某一条直线折叠,如果它能够与另一个图形完全 ,那么就说这两个图形关于这条直线(成轴)对称.这条直线叫做 .折叠后重合的点是对应点,叫做 .
注意:轴对称图形和轴对称的区别与联系.
对称点
对称轴
重合
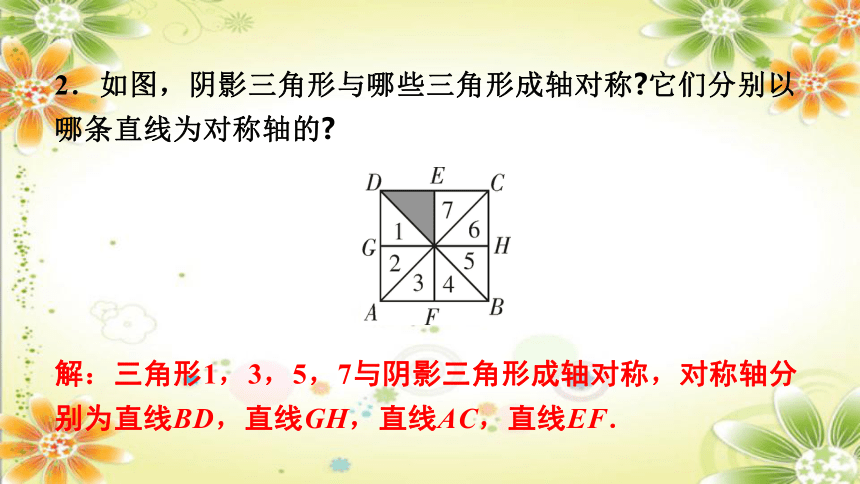
2.如图,阴影三角形与哪些三角形成轴对称 它们分别以哪条直线为对称轴的
解:三角形1,3,5,7与阴影三角形成轴对称,对称轴分别为直线BD,直线GH,直线AC,直线EF.
知识点三:轴对称的性质
(1)如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的 .
(2)轴对称图形的对称轴,是任何一对对应点所连线段的
.
垂直平分线
垂直平分线
A.AM=BM B.AP=BN
C.∠MAP=∠MBP D.∠ANM=∠BNM
3.如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )
B
A B C D
4.【例1】(跨学科融合、传统文化)(2022齐齐哈尔一模)汉字是中华民族智慧的结晶,是世界上独一无二的创造发明.在书写汉字的时候,我们能感受到汉字的演变之丰富,造型之奇美,内涵之厚重广博,其中有些汉字不乏对称之美,下列汉字中,是轴对称图形的是( )
D
小结:判断轴对称图形,关键是看能否找到一条直线,使图形沿着这条直线折叠后两旁互相重合.
小结:理解轴对称应抓住三点:(1)两个图形;(2)一条直线;(3)一个图形沿着这条直线对折后和另一个图形完全重合.
A B C D
5.【例2】下列图形中,△A'B'C'与△ABC关于直线MN成轴对称的是( )
B
小结:成轴对称的两个图形的对应线段相等,对应角相等.
A.4个 B.3个
C.2个 D.1个
6.【例3】如图,△ABC和△A'B'C'关于直线l对称,有下列结论:①△ABC≌△A'B'C';②∠BAC'=∠B'AC;③l垂直平分CC';④直线BC和B'C'的交点不一定在l上.其中正确的有( )
B
第(1)题图
7.【例4】(1)如图,∠A=30°,∠C'=60°,△ABC与△A'B'C'关于直线l对称,则∠B= ;
90°
小结:(1)成轴对称的两个图形全等;(2)轴对称图形被对称轴分成的两部分全等;(3)全等的两个图形不一定是轴对称图形.
第(2)题图
(2)(2021安庆模拟)如图,点D为△ABC的边AC上一点,点B,C关于DE对称,若AC=6,AD=2,则线段BD的长度为 .
4
A B C D
8.(跨学科融合、传统文化)(2022山西一模)平遥古城位于山西省中部平遥县内,始建于西周宣王时期,被称为“保存最为完好的四大古城”之一,也是中国仅有的以整座古城申报世界文化遗产获得成功的两座古城市之一.下列图标是古城内部分建筑的形象设计图,其中不属于轴对称图形的是( )
B
9.如图,按要求填序号:
(1)属于轴对称图形的有 ;
(2)两个图形成轴对称的有 .
②⑤⑥⑦⑨
①③④⑧⑩
A.AC=A'C'
B.AB∥B'C'
C.AA'⊥MN
D.BO=B'O
10.(人教8上P59)如图,若△ABC与△A'B'C'关于直线MN对称,BB'交MN于点O,则下列说法中不一定正确的是( )
B
(1)试写出两组对应相等的线段:
;
(2)试写出两组对应相等的角:
;
(3)线段AB,CD都被直线l .
垂直平分
∠BAC=∠ABD,∠ACD=∠BDC(答案不唯一)
★11.如图,直线l是该轴对称图形的对称轴.
AC=BD,AE=BE(答案不唯一)
小结:
1.概念:轴对称图形、两个图形关于某条直线对称、对称轴、对称点.
2.找轴对称图形的对称点.
3.垂直平分线.
谢 谢
第十三章 轴对称
轴对称
教学目标:
【知识与技能】
(1)理解轴对称图形和两个图形关于某条直线对称的概念.
(2)了解轴对称图形的对称轴,两个图形关于某条直线对称的对应点.
(3)掌握线段垂直平分线的概念.
(4)理解和掌握轴对称的性质.
【过程与方法】
通过已知图形画对称轴及画轴对称图形,让学生体会轴对称图形的性质和轴对称在实际生活中的应用.
【情感态度与价值观】
通过对轴对称图形和轴对称的认识,增强学生对对称美的认识,使学生感受数学带来的美.
教学重难点:
1轴对称图形和两个图形关于某条直线对称的概念.
2轴对称图形和两个图形关于某条直线对称的区别和联系.
1.(2022新课标)理解轴对称图形的概念.
2.(2022新课标)通过具体实例理解轴对称的概念,探索它的基本性质:成轴对称的两个图形中对应点的连线被对称轴垂直平分.
3.通过自己动手画、作、测量、计算和推理证明,体会轴对称的性质.
知识点一:轴对称图形
如果一个平面图形沿着一条直线折叠,直线两旁的部分能够 ,那么这个图形就叫做轴对称图形.
这条直线就是它的 .
对称轴
互相重合
A B C D
1.(跨学科融合)(2022青岛一模)2022年2月4日至20日,第24届冬奥会在北京和张家口举办,北京是唯一同时举办过夏季和冬季奥运会的城市.下列4个图形是四届冬奥会的部分图标,属于轴对称图形的是( )
C
知识点二:轴对称
把一个图形沿着某一条直线折叠,如果它能够与另一个图形完全 ,那么就说这两个图形关于这条直线(成轴)对称.这条直线叫做 .折叠后重合的点是对应点,叫做 .
注意:轴对称图形和轴对称的区别与联系.
对称点
对称轴
重合
2.如图,阴影三角形与哪些三角形成轴对称 它们分别以哪条直线为对称轴的
解:三角形1,3,5,7与阴影三角形成轴对称,对称轴分别为直线BD,直线GH,直线AC,直线EF.
知识点三:轴对称的性质
(1)如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的 .
(2)轴对称图形的对称轴,是任何一对对应点所连线段的
.
垂直平分线
垂直平分线
A.AM=BM B.AP=BN
C.∠MAP=∠MBP D.∠ANM=∠BNM
3.如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )
B
A B C D
4.【例1】(跨学科融合、传统文化)(2022齐齐哈尔一模)汉字是中华民族智慧的结晶,是世界上独一无二的创造发明.在书写汉字的时候,我们能感受到汉字的演变之丰富,造型之奇美,内涵之厚重广博,其中有些汉字不乏对称之美,下列汉字中,是轴对称图形的是( )
D
小结:判断轴对称图形,关键是看能否找到一条直线,使图形沿着这条直线折叠后两旁互相重合.
小结:理解轴对称应抓住三点:(1)两个图形;(2)一条直线;(3)一个图形沿着这条直线对折后和另一个图形完全重合.
A B C D
5.【例2】下列图形中,△A'B'C'与△ABC关于直线MN成轴对称的是( )
B
小结:成轴对称的两个图形的对应线段相等,对应角相等.
A.4个 B.3个
C.2个 D.1个
6.【例3】如图,△ABC和△A'B'C'关于直线l对称,有下列结论:①△ABC≌△A'B'C';②∠BAC'=∠B'AC;③l垂直平分CC';④直线BC和B'C'的交点不一定在l上.其中正确的有( )
B
第(1)题图
7.【例4】(1)如图,∠A=30°,∠C'=60°,△ABC与△A'B'C'关于直线l对称,则∠B= ;
90°
小结:(1)成轴对称的两个图形全等;(2)轴对称图形被对称轴分成的两部分全等;(3)全等的两个图形不一定是轴对称图形.
第(2)题图
(2)(2021安庆模拟)如图,点D为△ABC的边AC上一点,点B,C关于DE对称,若AC=6,AD=2,则线段BD的长度为 .
4
A B C D
8.(跨学科融合、传统文化)(2022山西一模)平遥古城位于山西省中部平遥县内,始建于西周宣王时期,被称为“保存最为完好的四大古城”之一,也是中国仅有的以整座古城申报世界文化遗产获得成功的两座古城市之一.下列图标是古城内部分建筑的形象设计图,其中不属于轴对称图形的是( )
B
9.如图,按要求填序号:
(1)属于轴对称图形的有 ;
(2)两个图形成轴对称的有 .
②⑤⑥⑦⑨
①③④⑧⑩
A.AC=A'C'
B.AB∥B'C'
C.AA'⊥MN
D.BO=B'O
10.(人教8上P59)如图,若△ABC与△A'B'C'关于直线MN对称,BB'交MN于点O,则下列说法中不一定正确的是( )
B
(1)试写出两组对应相等的线段:
;
(2)试写出两组对应相等的角:
;
(3)线段AB,CD都被直线l .
垂直平分
∠BAC=∠ABD,∠ACD=∠BDC(答案不唯一)
★11.如图,直线l是该轴对称图形的对称轴.
AC=BD,AE=BE(答案不唯一)
小结:
1.概念:轴对称图形、两个图形关于某条直线对称、对称轴、对称点.
2.找轴对称图形的对称点.
3.垂直平分线.
谢 谢
