人教版高中数学选择性必修第一册3.1.2 第一课时 椭圆的简单几何性质 课件(共44张PPT)
文档属性
| 名称 | 人教版高中数学选择性必修第一册3.1.2 第一课时 椭圆的简单几何性质 课件(共44张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 00:00:00 | ||
图片预览











文档简介
(共44张PPT)
3.1.2 椭圆的简单几何性质
第一课时 椭圆的简单几何性质
[学习目标]
1.掌握椭圆的几何图形和简单几何性质.
2.掌握椭圆的标准方程中a,b,c及离心率e的几何意义和它们之间的相互关系.
必备知识 自主探究
关键能力 互动探究
课时作业 巩固提升
A
B
3a2=4b2
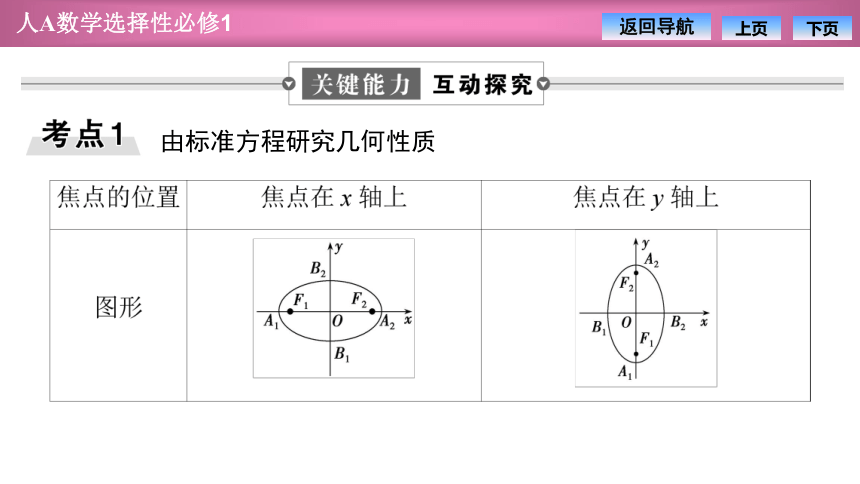
由标准方程研究几何性质
-a≤x≤a,-b≤y≤b
-b≤x≤b,-a≤y≤a
A1(-a,0),A2(a,0),
B1(0,-b),B2(0,b)
A1(0,-a),A2(0,a),
B1(-b,0),B2(b,0)
2b
2a
焦点的位置 焦点在x轴上 焦点在y轴上
焦点 __________________ ______________________
焦距 |F1F2|=___
对称性 对称轴 ,对称中心______
离心率
e=____
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
2c
坐标轴
原点
[例1] 求椭圆9x2+16y2=144的长轴长、短轴长、离心率、焦点和顶点的坐标.
由椭圆方程讨论其几何性质的步骤
(1)化椭圆方程为标准形式,确定焦点在哪个轴上.
(2)由标准形式求a,b,c,写出其几何性质.
1.求椭圆x2+9y2=81的长轴长、短轴长、离心率、焦点和顶点的坐标.
利用椭圆的几何性质求椭圆的标准方程时,通常采用待定系数法,其步骤是:
(1)确定焦点位置.
(2)设出相应椭圆的标准方程(对于焦点位置不确定的椭圆可能有两种标准方程).
(3)根据已知条件构造关于参数的关系式,利用方程(组)求参数,从而求出方程.
2.求满足下列条件的椭圆的标准方程:
(2)短轴的一个端点到一个焦点的距离为5,焦点到椭圆中心的距离为3;
椭圆的离心率
2.椭圆离心率对椭圆形状的影响
0<e<1
[解析] 如图所示.
3.求椭圆离心率的取值范围的方法
(1)建立目标函数,运用求函数值域的方法求解;
(2)建立目标变量的不等式,解不等式求解;
(3)解题时用基本量表示出椭圆上的点的坐标后,借助椭圆的范围(|x|≤a,|y|≤b)建立一个关于基本量的不等式组.
3.已知F1,F2是椭圆的两个焦点,过F1且与椭圆长轴垂直的直线交椭圆于A,B两点,若△ABF2是等腰直角三角形,求该椭圆的离心率.
椭圆的第二定义
定点F
定直线l
常数e
4.点M与定点F(2,0)的距离和它到定直线x=8的距离的比是1∶2,求点M的轨迹方程,并说明轨迹是什么图形?
1.知识清单:(1)椭圆的简单几何性质.
(2)由标准方程研究几何性质.
(3)由几何性质研究标准方程.
(4)求椭圆的离心率.
(5)椭圆的第二定义.
2.方法归纳:待定系数法、直接法求轨迹方程.
3.常见误区:(1)对椭圆的长轴长容易写为a.
课时作业 巩固提升
3.1.2 椭圆的简单几何性质
第一课时 椭圆的简单几何性质
[学习目标]
1.掌握椭圆的几何图形和简单几何性质.
2.掌握椭圆的标准方程中a,b,c及离心率e的几何意义和它们之间的相互关系.
必备知识 自主探究
关键能力 互动探究
课时作业 巩固提升
A
B
3a2=4b2
由标准方程研究几何性质
-a≤x≤a,-b≤y≤b
-b≤x≤b,-a≤y≤a
A1(-a,0),A2(a,0),
B1(0,-b),B2(0,b)
A1(0,-a),A2(0,a),
B1(-b,0),B2(b,0)
2b
2a
焦点的位置 焦点在x轴上 焦点在y轴上
焦点 __________________ ______________________
焦距 |F1F2|=___
对称性 对称轴 ,对称中心______
离心率
e=____
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
2c
坐标轴
原点
[例1] 求椭圆9x2+16y2=144的长轴长、短轴长、离心率、焦点和顶点的坐标.
由椭圆方程讨论其几何性质的步骤
(1)化椭圆方程为标准形式,确定焦点在哪个轴上.
(2)由标准形式求a,b,c,写出其几何性质.
1.求椭圆x2+9y2=81的长轴长、短轴长、离心率、焦点和顶点的坐标.
利用椭圆的几何性质求椭圆的标准方程时,通常采用待定系数法,其步骤是:
(1)确定焦点位置.
(2)设出相应椭圆的标准方程(对于焦点位置不确定的椭圆可能有两种标准方程).
(3)根据已知条件构造关于参数的关系式,利用方程(组)求参数,从而求出方程.
2.求满足下列条件的椭圆的标准方程:
(2)短轴的一个端点到一个焦点的距离为5,焦点到椭圆中心的距离为3;
椭圆的离心率
2.椭圆离心率对椭圆形状的影响
0<e<1
[解析] 如图所示.
3.求椭圆离心率的取值范围的方法
(1)建立目标函数,运用求函数值域的方法求解;
(2)建立目标变量的不等式,解不等式求解;
(3)解题时用基本量表示出椭圆上的点的坐标后,借助椭圆的范围(|x|≤a,|y|≤b)建立一个关于基本量的不等式组.
3.已知F1,F2是椭圆的两个焦点,过F1且与椭圆长轴垂直的直线交椭圆于A,B两点,若△ABF2是等腰直角三角形,求该椭圆的离心率.
椭圆的第二定义
定点F
定直线l
常数e
4.点M与定点F(2,0)的距离和它到定直线x=8的距离的比是1∶2,求点M的轨迹方程,并说明轨迹是什么图形?
1.知识清单:(1)椭圆的简单几何性质.
(2)由标准方程研究几何性质.
(3)由几何性质研究标准方程.
(4)求椭圆的离心率.
(5)椭圆的第二定义.
2.方法归纳:待定系数法、直接法求轨迹方程.
3.常见误区:(1)对椭圆的长轴长容易写为a.
课时作业 巩固提升
