2023-2024学年人教版八年级数学上册第十三章 轴对称:13.2画轴对称图形(1) 课件 23张PPT
文档属性
| 名称 | 2023-2024学年人教版八年级数学上册第十三章 轴对称:13.2画轴对称图形(1) 课件 23张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 530.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
第十三章 轴对称
画轴对称图形(1)
教学目标:
【知识与技能】
通过实际操作,掌握画轴对称图形的方法.
【过程与方法】
探索画一般的轴对称图形的方法,使学生能够按要求作出简单平面图形经过一次对称后的图形.
【情感态度与价值观】
培养学生的审美情趣、合作意识和学习兴趣.
教学重难点:
1能够按要求作出简单平面图形经过一次对称后的图形.
2较复杂图形的轴对称图形的画法.
1.(2022新课标)能画出简单平面图形(点、线段、直线、三角形等)关于给定对称轴的对称图形.
2.(2022新课标)认识并欣赏自然界和现实生活中的轴对称图形.
3.理解图形轴对称变换的性质.
A B C D
知识点一:补全轴对称图形
如图,阴影部分是由5个小正方形涂黑组成的一个直角图形,再将方格内空白的两个小正方形涂黑,得到新的图形(阴影部分),其中不是轴对称图形的是( )
D
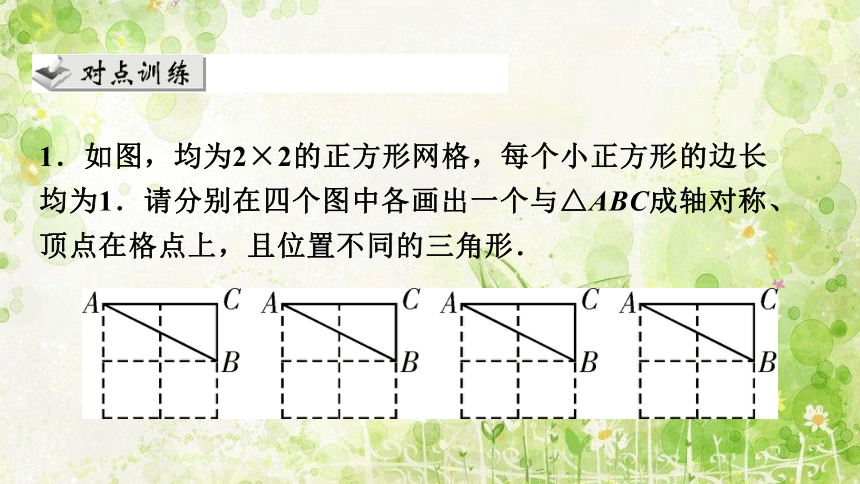
1.如图,均为2×2的正方形网格,每个小正方形的边长均为1.请分别在四个图中各画出一个与△ABC成轴对称、顶点在格点上,且位置不同的三角形.
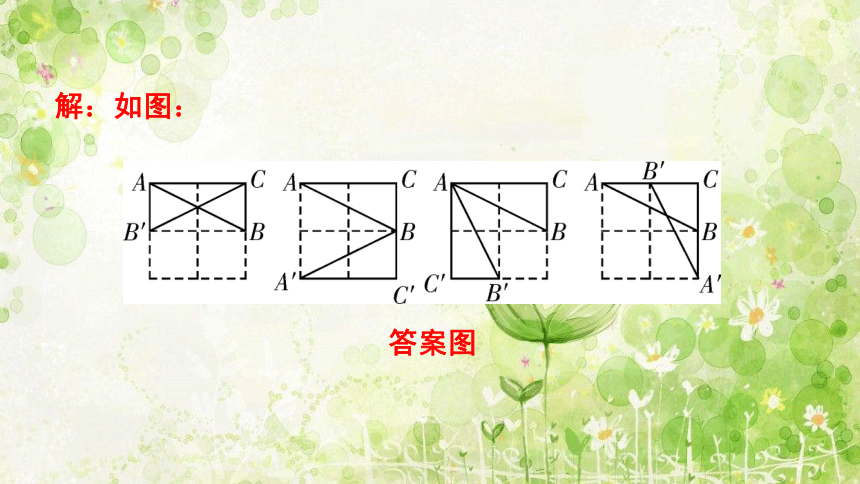
解:如图:
答案图
知识点二:图形轴对称变换的性质
(1)成轴对称的两个图形 ;
(2)对称轴与连接对应点的线段 ;
(3)对应点到对称轴的距离 ;
(4)对应点的连线互相 .
平行
相等
垂直
全等
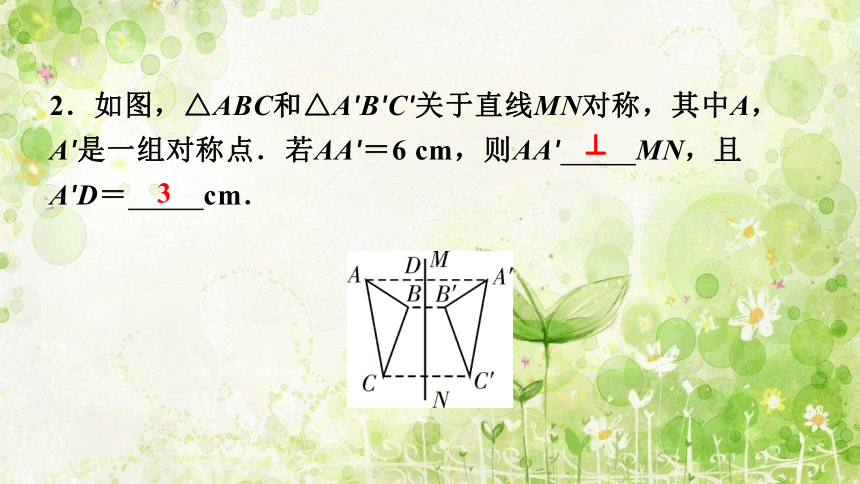
2.如图,△ABC和△A'B'C'关于直线MN对称,其中A,A'是一组对称点.若AA'=6 cm,则AA' MN,且
A'D= cm.
3
⊥
知识点三:画出一个平面图形关于某直线对称的图形
要作出一个图形关于某直线成轴对称的图形,只需根据图形作出各顶点的 ,再顺次连接各 .
对称点
对称点
3.(人教8上P68)画出△ABC关于直线l的对称图形.
解:如图,△A'B'C即为所求.
答案图
4.【例1】如图,一轴对称图形画出了它的一半,请你以中间直线为对称轴画出它的另一半.
解:如图:
答案图
小结:在格点上找出对称点,再连接成图.
5.【例2】如图,把图形补画成轴对称图形.
解:如图:
答案图
小结:作出关键点的对称点,本题中A,C均在对称轴上,作出B的对称点即可.
6.【例3】如图,以虚线为对称轴,画出已知图形的轴对称图形.
找出点A,B关于已知直线对称点的位置,连接即可,图略.
小结:过特殊点作垂直,取对应点,再依次连接.
7.【例4】如图,已知△ABC和直线MN,求作△A'B'C',使△A'B'C'和△ABC关于直线MN对称.(不要求写作法,只保留作图痕迹)
解:从三角形的三个顶点,分别向MN作垂线,并延长相同距离,得到三个对应点,顺次连接就是所求的轴对称图形.如图:
小结:(1)点在对称轴上时,它关于对称轴的对称点是它本身;(2)点在对称轴一侧时,它关于对称轴的对称点在对称轴的另一侧.
8.如图是由三个小正方形组成的图形,请你在图中补画一个小正方形,使补画后的图形为轴对称图形.
解:如图(答案不唯一):
答案图
9.如图,把图形补画成轴对称图形.
解:如图:
答案图
10.(人教8上P67)如图,画出△ABC关于直线MN对称的图形.
找出点A,B,C关于直线MN的对称点的位置,然后顺次连接即可.图略.
★11.如图,请作出四边形ABCD关于直线a的轴对称图形.(不写作法,但必须保留作图痕迹)
解:如图,四边形A'B'C'D'即为所求.
小结:
1.由一个平面图形可以得到与它关于一条直线对称的图形,这个图形与原图形的形状、大小完全相同.
2.经过轴对称变换的图形与原图形上的对应点的连线被对称轴垂直平分.
3.画一个图形的轴对称图形,关键是找到图形上一些特殊点的对称点,它的方法如下:
(1)由已知点出发作已知直线的垂线,并确定垂足;
(2)在直线的另一侧,以垂足为一端点,作一条线段使之等于已知点和垂足之间的线段的长,得到线段的另一端点,即为对称点;
(3)连接这些对称点,就得到原图形的轴对称图形.
谢 谢
第十三章 轴对称
画轴对称图形(1)
教学目标:
【知识与技能】
通过实际操作,掌握画轴对称图形的方法.
【过程与方法】
探索画一般的轴对称图形的方法,使学生能够按要求作出简单平面图形经过一次对称后的图形.
【情感态度与价值观】
培养学生的审美情趣、合作意识和学习兴趣.
教学重难点:
1能够按要求作出简单平面图形经过一次对称后的图形.
2较复杂图形的轴对称图形的画法.
1.(2022新课标)能画出简单平面图形(点、线段、直线、三角形等)关于给定对称轴的对称图形.
2.(2022新课标)认识并欣赏自然界和现实生活中的轴对称图形.
3.理解图形轴对称变换的性质.
A B C D
知识点一:补全轴对称图形
如图,阴影部分是由5个小正方形涂黑组成的一个直角图形,再将方格内空白的两个小正方形涂黑,得到新的图形(阴影部分),其中不是轴对称图形的是( )
D
1.如图,均为2×2的正方形网格,每个小正方形的边长均为1.请分别在四个图中各画出一个与△ABC成轴对称、顶点在格点上,且位置不同的三角形.
解:如图:
答案图
知识点二:图形轴对称变换的性质
(1)成轴对称的两个图形 ;
(2)对称轴与连接对应点的线段 ;
(3)对应点到对称轴的距离 ;
(4)对应点的连线互相 .
平行
相等
垂直
全等
2.如图,△ABC和△A'B'C'关于直线MN对称,其中A,A'是一组对称点.若AA'=6 cm,则AA' MN,且
A'D= cm.
3
⊥
知识点三:画出一个平面图形关于某直线对称的图形
要作出一个图形关于某直线成轴对称的图形,只需根据图形作出各顶点的 ,再顺次连接各 .
对称点
对称点
3.(人教8上P68)画出△ABC关于直线l的对称图形.
解:如图,△A'B'C即为所求.
答案图
4.【例1】如图,一轴对称图形画出了它的一半,请你以中间直线为对称轴画出它的另一半.
解:如图:
答案图
小结:在格点上找出对称点,再连接成图.
5.【例2】如图,把图形补画成轴对称图形.
解:如图:
答案图
小结:作出关键点的对称点,本题中A,C均在对称轴上,作出B的对称点即可.
6.【例3】如图,以虚线为对称轴,画出已知图形的轴对称图形.
找出点A,B关于已知直线对称点的位置,连接即可,图略.
小结:过特殊点作垂直,取对应点,再依次连接.
7.【例4】如图,已知△ABC和直线MN,求作△A'B'C',使△A'B'C'和△ABC关于直线MN对称.(不要求写作法,只保留作图痕迹)
解:从三角形的三个顶点,分别向MN作垂线,并延长相同距离,得到三个对应点,顺次连接就是所求的轴对称图形.如图:
小结:(1)点在对称轴上时,它关于对称轴的对称点是它本身;(2)点在对称轴一侧时,它关于对称轴的对称点在对称轴的另一侧.
8.如图是由三个小正方形组成的图形,请你在图中补画一个小正方形,使补画后的图形为轴对称图形.
解:如图(答案不唯一):
答案图
9.如图,把图形补画成轴对称图形.
解:如图:
答案图
10.(人教8上P67)如图,画出△ABC关于直线MN对称的图形.
找出点A,B,C关于直线MN的对称点的位置,然后顺次连接即可.图略.
★11.如图,请作出四边形ABCD关于直线a的轴对称图形.(不写作法,但必须保留作图痕迹)
解:如图,四边形A'B'C'D'即为所求.
小结:
1.由一个平面图形可以得到与它关于一条直线对称的图形,这个图形与原图形的形状、大小完全相同.
2.经过轴对称变换的图形与原图形上的对应点的连线被对称轴垂直平分.
3.画一个图形的轴对称图形,关键是找到图形上一些特殊点的对称点,它的方法如下:
(1)由已知点出发作已知直线的垂线,并确定垂足;
(2)在直线的另一侧,以垂足为一端点,作一条线段使之等于已知点和垂足之间的线段的长,得到线段的另一端点,即为对称点;
(3)连接这些对称点,就得到原图形的轴对称图形.
谢 谢
