2023-2024学年人教版八年级数学上册13.1.2线段的垂直平分线的性质(2) 课件 23张PPT
文档属性
| 名称 | 2023-2024学年人教版八年级数学上册13.1.2线段的垂直平分线的性质(2) 课件 23张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
第十三章 轴对称
线段的垂直平分线的性质(2)
教学目标:
【知识与技能】
(1)会画线段的垂直平分线.
(2)会画轴对称图形的对称轴.
【过程与方法】
通过已知图形画对称轴,让学生体会轴对称图形的性质和轴对称在实际生活中的应用.
【情感态度与价值观】
通过对轴对称图形的认识,增强学生对对称美的认识,使学生感受数学带来的美的享受.
教学重难点:
1轴对称图形的对称轴的画法.
2轴对称图形的对称轴的画法.
1.(2022新课标)能用尺规作图:作一条线段的垂直平分线;过一点作已知直线的垂线.
2.能用尺规作轴对称图形及成轴对称的两个图形的对称轴.
3.通过自己动手画、作、测量、计算和推理证明,进一步感知线段垂直平分线的性质.
知识点一:作已知线段的垂直平分线
用尺规作图作出线段的垂直平分线.
如图,已知线段AB,求作AB的垂直平分线.
作法:分别以A和B为圆心,以大于AB 的长为半径画弧,两弧相交于C,D两点,连接CD,即为AB的垂直平分线.
1.如图,已知线段AB,用尺规作出它的垂直平分线CD,并标出线段的中点O.
图略
A B C D
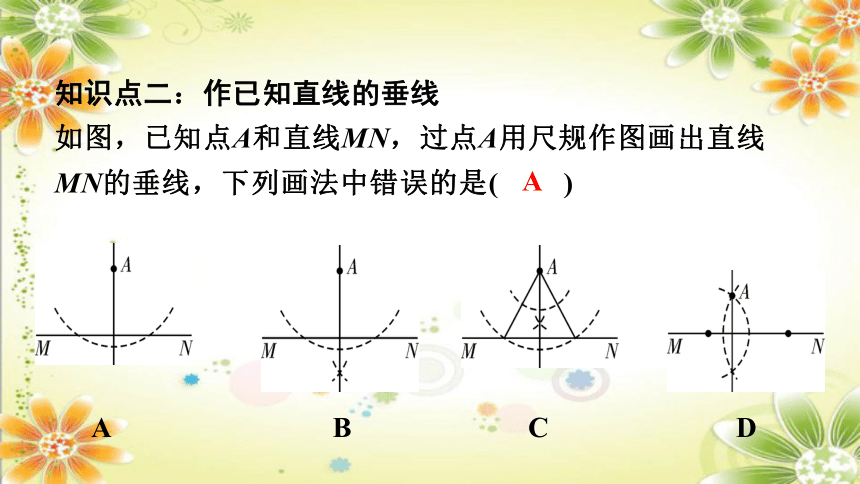
知识点二:作已知直线的垂线
如图,已知点A和直线MN,过点A用尺规作图画出直线MN的垂线,下列画法中错误的是( )
A
2.如图,已知直线l和l外一点P,用尺规作l的垂线,使它经过点P.
图略
知识点三:作对称轴
作轴对称图形或者成轴对称的两个图形的对称轴的方法:
首先连接两个 ,然后作所连线段的
.
垂直平分线
对应点
3.如图,△ABC与△DEF关于直线l对称,请仅用无刻度的直尺,在下面两个图中分别作出直线l.
解:如图:
4.【例1】(人教8上P63、北师7下P124)如图,已知线段AB,请用直尺和圆规作出线段AB的对称轴.
解:如图,直线EF就是线段AB的对称轴.
小结:作线段的对称轴,实质是作线段的垂直平分线.
5.【例2】(人教8上P64、北师7下P131)如图,利用尺规作图,画出下列轴对称图形的一条对称轴.
小结:画轴对称图形的对称轴,实际上就是作出垂直平分线.
图略
6.【例3】如图,△ABC与△A'B'C'关于某一直线对称.
(1)用尺规作图法作出对称轴;
(2)延长各对对应线段,观察它们的交点在什么位置上 从而得到什么结论
解:(1)连接其中一对对应点,作所连线段的垂直平分线即为对称轴.图略.
(2)图略,交点在对称轴上.结论:关于某一直线对称的两个图形,对应线段如果不平行,那么它们所在的直线的交点在对称轴上.
小结:连接任一对对应点,再作垂直平分线,就可以得到对称轴.
7.【例4】(人教8上P66、北师8下P24)已知公路l的同旁有两个村庄A,B,要在公路旁边建一个公交车上落站,使上落站到两个村庄的距离相等,请确定上落站的位置.
解:连接AB,作AB的垂直平分线交直线l于点P,则点P为上落站的位置.图略.
小结:由实际问题抽象出到两个点相等的问题,运用垂直平分线的性质定理,并作图.
8.如图,点A和点B关于某条直线成轴对称,你能作出这条直线吗 如果可以,请作图.
可以,图略.
9.如图,指出下列轴对称图形各有几条对称轴,并把它们画出来.
1条,2条,2条,4条,图略.
10.如图,△ABC和△DEF关于某直线成轴对称,你能作出这条直线吗
解:如图,l即为所求.
答案图
★11.(跨学科融合)(人教8上P66、北师8下P30)如图,电信部门要在S区修建一座电视信号发射塔.按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路m和n的距离也必须相等.发射塔应修建在什么位置 在图上标出它的位置.
解:如图,发射塔应修建在点P的位置.
课堂小结:
画轴对称图形的对称轴,实际上就是运用轴对称的性质,找到对应点所连线段的垂直平分线.
谢谢大家
第十三章 轴对称
线段的垂直平分线的性质(2)
教学目标:
【知识与技能】
(1)会画线段的垂直平分线.
(2)会画轴对称图形的对称轴.
【过程与方法】
通过已知图形画对称轴,让学生体会轴对称图形的性质和轴对称在实际生活中的应用.
【情感态度与价值观】
通过对轴对称图形的认识,增强学生对对称美的认识,使学生感受数学带来的美的享受.
教学重难点:
1轴对称图形的对称轴的画法.
2轴对称图形的对称轴的画法.
1.(2022新课标)能用尺规作图:作一条线段的垂直平分线;过一点作已知直线的垂线.
2.能用尺规作轴对称图形及成轴对称的两个图形的对称轴.
3.通过自己动手画、作、测量、计算和推理证明,进一步感知线段垂直平分线的性质.
知识点一:作已知线段的垂直平分线
用尺规作图作出线段的垂直平分线.
如图,已知线段AB,求作AB的垂直平分线.
作法:分别以A和B为圆心,以大于AB 的长为半径画弧,两弧相交于C,D两点,连接CD,即为AB的垂直平分线.
1.如图,已知线段AB,用尺规作出它的垂直平分线CD,并标出线段的中点O.
图略
A B C D
知识点二:作已知直线的垂线
如图,已知点A和直线MN,过点A用尺规作图画出直线MN的垂线,下列画法中错误的是( )
A
2.如图,已知直线l和l外一点P,用尺规作l的垂线,使它经过点P.
图略
知识点三:作对称轴
作轴对称图形或者成轴对称的两个图形的对称轴的方法:
首先连接两个 ,然后作所连线段的
.
垂直平分线
对应点
3.如图,△ABC与△DEF关于直线l对称,请仅用无刻度的直尺,在下面两个图中分别作出直线l.
解:如图:
4.【例1】(人教8上P63、北师7下P124)如图,已知线段AB,请用直尺和圆规作出线段AB的对称轴.
解:如图,直线EF就是线段AB的对称轴.
小结:作线段的对称轴,实质是作线段的垂直平分线.
5.【例2】(人教8上P64、北师7下P131)如图,利用尺规作图,画出下列轴对称图形的一条对称轴.
小结:画轴对称图形的对称轴,实际上就是作出垂直平分线.
图略
6.【例3】如图,△ABC与△A'B'C'关于某一直线对称.
(1)用尺规作图法作出对称轴;
(2)延长各对对应线段,观察它们的交点在什么位置上 从而得到什么结论
解:(1)连接其中一对对应点,作所连线段的垂直平分线即为对称轴.图略.
(2)图略,交点在对称轴上.结论:关于某一直线对称的两个图形,对应线段如果不平行,那么它们所在的直线的交点在对称轴上.
小结:连接任一对对应点,再作垂直平分线,就可以得到对称轴.
7.【例4】(人教8上P66、北师8下P24)已知公路l的同旁有两个村庄A,B,要在公路旁边建一个公交车上落站,使上落站到两个村庄的距离相等,请确定上落站的位置.
解:连接AB,作AB的垂直平分线交直线l于点P,则点P为上落站的位置.图略.
小结:由实际问题抽象出到两个点相等的问题,运用垂直平分线的性质定理,并作图.
8.如图,点A和点B关于某条直线成轴对称,你能作出这条直线吗 如果可以,请作图.
可以,图略.
9.如图,指出下列轴对称图形各有几条对称轴,并把它们画出来.
1条,2条,2条,4条,图略.
10.如图,△ABC和△DEF关于某直线成轴对称,你能作出这条直线吗
解:如图,l即为所求.
答案图
★11.(跨学科融合)(人教8上P66、北师8下P30)如图,电信部门要在S区修建一座电视信号发射塔.按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路m和n的距离也必须相等.发射塔应修建在什么位置 在图上标出它的位置.
解:如图,发射塔应修建在点P的位置.
课堂小结:
画轴对称图形的对称轴,实际上就是运用轴对称的性质,找到对应点所连线段的垂直平分线.
谢谢大家
