七年级数学上册试题 第三章 《整式及其加减》单元测试-北师大版(含答案)
文档属性
| 名称 | 七年级数学上册试题 第三章 《整式及其加减》单元测试-北师大版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 453.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 00:00:00 | ||
图片预览




文档简介
第三章 《整式及其加减》单元测试
一、选择题(本大题共10个小题,每小题3分,共30分;)
1.下列各式:2m,0,-2n,,中,代数式有( ).
A.4个 B.5个 C.6个 D.7个
2.若=3,,且x>y,则x+y的值是( )
A.和 B.3和 C.和9 D. 和3
3.某市居民生活用水收费标准如下:若每月用水量不超过5吨水(包括5吨水),每吨水收费m元;若每月用水量超过5吨水,超过的部分每吨水收费元.已知小明家2021年6月份用水12吨,那么小明家应缴纳水费为( )
A.元 B.元 C.元 D.元
4.某商店促销的方法是将原价x元的衣服以(0.8x﹣10)元出售,意思是( )
A.原价减去10元后再打8折 B.原价打8折后再减去10元
C.原价减去10元后再打2折 D.原价打2折后再减去10元
5.下列说法中,正确的是( )
A.单项的系数是 B.单项式的次数为
C.多项式是二次多项式 D.多项式的常数项是7
6.按一定规律排列的单项式:2x,-3x2,4x3,-5x4,6x5,-7x6,…第n个单项式是( )
A. B. C. D.
7.已知a﹣b=2,a﹣c=,则代数式(b﹣c)2+3(b﹣c)+的值是( )
A.﹣ B. C.0 D.
8.下列运算,结果正确的是( )
A.a3+d3=a6 B.2ab﹣ab=2
C.5a2b﹣2ba2=3a2b D.x4﹣x3=x
9.如图,两个正方形的面积分别为16,9,两阴影部分的面积分别为,,则等于( )
A.8 B.7 C.6 D.5
10.如图,点O在直线AB上,点A1,A2,A3,…在射线OA上,点B1,B2,B3,…在射线OB上,图中的每一个实线段和虚线段的长均为1个单位长度.一个动点M从O点出发,按如图所示的箭头方向沿着实线段和以O为圆心的半圆匀速运动,速度为每秒1个单位长度.按此规律,则动点M到达A101点处所需时间为( )秒.
A.5 050π B.5 050π+101 C.5 055π D.5 055π+101
二、填空题(本大题共6个小题,每题3分,共18分)
11.一种商品每件成本为元,现按成本增加20%出售,则这件商品的售价为__________元(用含有的式子表示).
12.若,则代数式的值为________.
13.若a、b互为相反数,c、d互为倒数,m是的相反数,则的值是_________.
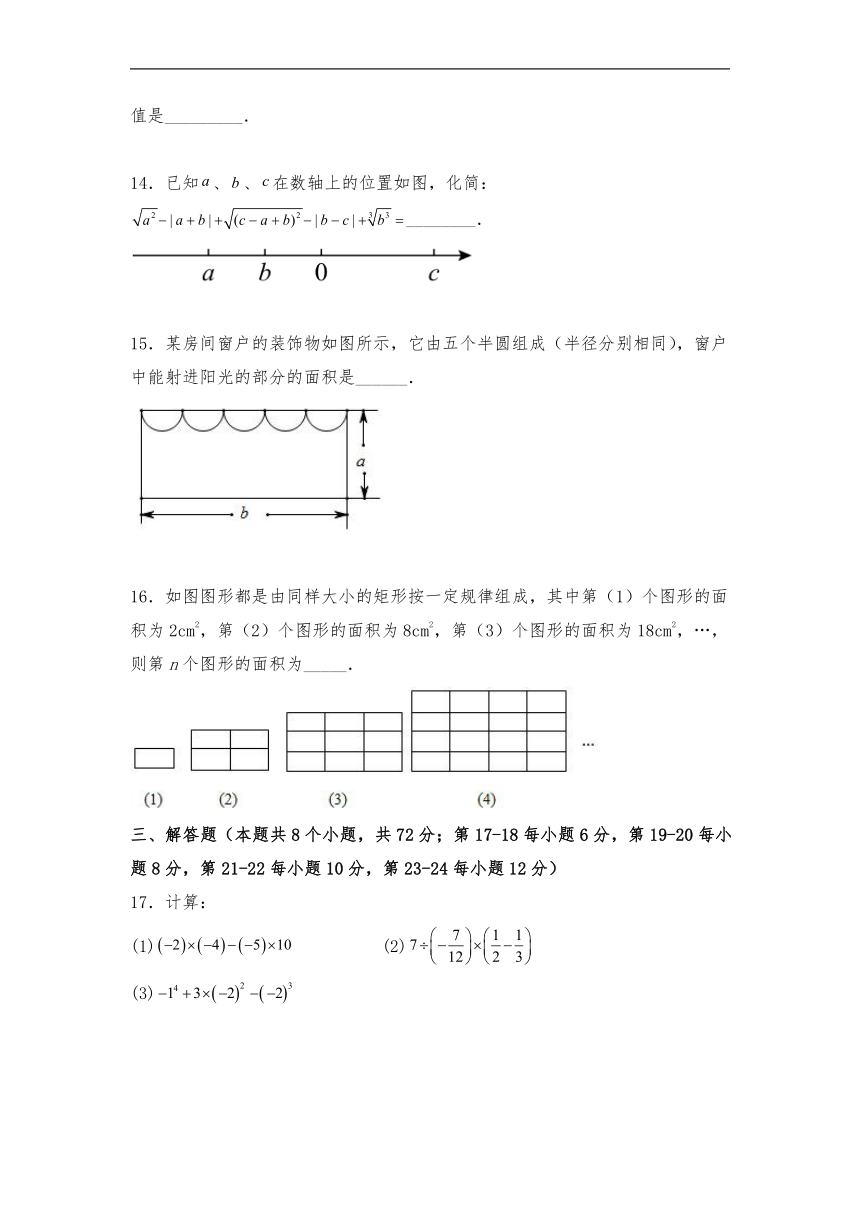
14.已知、、在数轴上的位置如图,化简:________.
15.某房间窗户的装饰物如图所示,它由五个半圆组成(半径分别相同),窗户中能射进阳光的部分的面积是______.
16.如图图形都是由同样大小的矩形按一定规律组成,其中第(1)个图形的面积为2cm2,第(2)个图形的面积为8cm2,第(3)个图形的面积为18cm2,…,则第n个图形的面积为_____.
三、解答题(本题共8个小题,共72分;第17-18每小题6分,第19-20每小题8分,第21-22每小题10分,第23-24每小题12分)
17.计算:
(1) (2) (3)
(4) (5) (6)
18.化简并求值:,其中、的取值如图所示.
19.一张边长为x米的正方形铁皮,左边两个角都剪去边长为0.1米的正方形,右边两个角都剪去一边长为0.1米的长方形,如图1所示,将四周折起,做成一个底与盖一样大的长方体铁盒.
(1)请用含x的代数式分别表示铁盒底面长方形的长和宽,并计算长是宽的多少倍?
(2)若x=0.5米,问这个铁盒能否装得下5升(立方分米)液体?请说明理由;
(3)如图2所示,若该铁盒装满了一层高为0.1米的圆柱形易拉罐,求该铁盒空间的利用率(易拉罐总体积与铁盒容积的比).
20.如图,正方形ABCD与正方形BFGE中,点E在边AB上,若AE=a,BE=b,(其中a>2b).
(1)请用含有a,b的代数式表示图中阴影部分的面积;
(2)当a=5cm,b=3cm时,求阴影部分的面积.
21.如图图案是用长度相同的火柴棒按一定规律拼搭而成,图案需8根火柴棒,图案②需15根火柴棒,图案②需15根火柴棒,…
(1)按此规律,图案⑦需____________根火柴棒;
(2)用含n的代数式表示第n个图案需根火柴棒根数.
22.如图,长为60cm,宽为的大长方形被分割为7小块,除阴影A、B外,其余5块是形状大小完全相同的小长方形,其中小长方形的较短一边长度为10cm.
(1)从图可知,每块小长方形的较长的一边长度是_________cm.代数式,中,哪一个代数式的值为正数?_______________.
(2)请你先用含的代数式表示阴影A、B的面积,并说明阴影A的面积一定比阴影B的面积大.
(3)设阴影A和B的面积之和为,阴影A和B的周长之和为,问代数式“S-C”的值可能是负数吗?请你先作出判断,并说明理由.
23.为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的,该市自来水收费标准(按月结算)如表所示:
每月用水量 单价
不超出6的部分 2元/
超出6不超出10的部分 4元/
超出10的部分 8元/
例如:若某户居民1月份用水8,则应收水费:2×6+4×(8﹣6)=20(元).
(1)若该户居民2月份用水12.5,则应收水费 元.
(2)若该户居民3月份用水a(其中6<a<10),则应收水费多少元?(用含a的整式表示,并化简)
(3)若该户居民4月份用水x,4、5两个月共用水15,且5月份用水超过4月份,请用含x的整式表示4、5两个月共交的水费 ,并化简.
24.已知多项式是关于的二次多项式,且二次项系数为,数轴上两点对应的数分别为.
(1)______,______,线段______;
(2)若数轴上有一点,使得,点为的中点,求的长;
(3)有一动点从点出发,以1个单位每秒的速度向终点运动,同时动点从点出发,以个单位每秒的速度在数轴上作同向运动,设运动时间为秒(),点为线段的中点,点为线段的中点,点在线段上且,在的运动过程中,求的值.
答案
一、选择题
C.A.B.B.C.D.C.C.B.B.
二、填空题
11.1.2a.
12.-1
13.4
14.
15.
16.
三、解答题
17.(1)解:原式
;
(2)原式
;
(3)原式
;
(4)原式
;
(5)原式
;
(6)原式
.
18.解:
=
=
=
根据数轴可知,,把,代入得:
原式=.
19.解:
(1) 铁盒底面长方形的长是x-0.1×2=(x-0.2)米,宽是(x-0.1×2)÷2=(0.5x-0.1)米,
(x-0.2)÷(0.5x-0.1)=2.
故长是宽的2倍.
(2) 当x=0.5米时,
(x-0.2)×(0.5x-0.1)×0.1
=(0.5-0.2)×(0.5×0.5-0.1)×0.1
=0.3×0.15×0.1
=0.0045(立方米),
0.0045立方米=4.5升,
4.5升<5升
故这个铁盒不能装得下5升(立方分米)液体.
(3) )[π×(x÷2)2]÷x2=.
故该铁盒空间的利用率是.
20.(1)阴影部分面积的面积=△ABC的面积-△AEG的面积-正方形EBFG的面积-△CFG的面积==;
(2)把a=5,b=3代入上式得:
阴影部分的面积==8(cm2)
答:阴影部分面积是8cm2.
21.(1)解:∵图案①需火柴棒:8根;
图案②需火柴棒:8+7=15根;
图案③需火柴棒:8+7+7=22根;
…
图案⑦需火柴棒:8+7×6=50根;
故答案为:50;
(2)解:由(1)中规律:
图案n需火柴棒:8+7(n-1)=7n+1根;
故答案为:7n+1;
22.(1)解:观察图形可得,小长方形的较长的边为:(厘米),
∴(x-30)为B的较短的一边长,为正数,
故答案为:30;.
(2)解:由图可得,
,
∴阴影A的面积一定比阴影B的面积大.
(3)解:“S-C”的值不可能是负数,理由如下:
由(2)得
,
由图可得
,
∴
,
由图形可得当x最小但不等于30cm时,,
当x最大但不等于40cm时,,
故“S-C”的值不可能是负数.
23.(1)解:应收水费=2×6+4×(10﹣6)+8×(12.5﹣10)=48(元),
故答案为:48;
(2)解:应收水费=不超过6的部分的水费+超出6不超出10部分的水费,
∴应收水费为6×2+4(a﹣6)=(4a﹣12)元,
∴应收水费为(4a﹣12)元;
(3)解:因为5月份用水量超过了4月份,所以4月份用水量少于7.5.
①当4月份用水量少于5时,则5月份用水量超过10,
∴4,5两个月共交水费=2x+8(15﹣x﹣10)+4×4+6×2=(﹣6x+68)元;
②当4月份用水量大于或等于5但不超过6时,则5月份用水量不少于9但不超过10,
∴4、5两个月共交水费=2x+4(15﹣x﹣6)+6×2=(﹣2x+48)元;
③当4月份用水量超过6但少于7.5时,则5月份用水量超过7.5但少于9,
∴4,5两个月共交水费=4(x﹣6)+6×2+4(15﹣x﹣6)+6×2=36(元).
综上所述,当 时,4、5两个月共交的水费为(-6x+68)元;当时,4、5两个月共交的水费为(-2x+48)元;当时,4、5两个月共交的水费为36元.
24.(1).
(2)①当在AB之间时,如图.
若.则.
.
为中点 .
.
②当在延长线上时,如图.
若.则.
.
为中点.
.
.综上或75.
(3)
由题得,对应的数为.对应的数为.
为中点,.
同理,为中点,则.
在上且.且.
对应的数为.
为中点,在上,且.
在右侧.
.
.
.
一、选择题(本大题共10个小题,每小题3分,共30分;)
1.下列各式:2m,0,-2n,,中,代数式有( ).
A.4个 B.5个 C.6个 D.7个
2.若=3,,且x>y,则x+y的值是( )
A.和 B.3和 C.和9 D. 和3
3.某市居民生活用水收费标准如下:若每月用水量不超过5吨水(包括5吨水),每吨水收费m元;若每月用水量超过5吨水,超过的部分每吨水收费元.已知小明家2021年6月份用水12吨,那么小明家应缴纳水费为( )
A.元 B.元 C.元 D.元
4.某商店促销的方法是将原价x元的衣服以(0.8x﹣10)元出售,意思是( )
A.原价减去10元后再打8折 B.原价打8折后再减去10元
C.原价减去10元后再打2折 D.原价打2折后再减去10元
5.下列说法中,正确的是( )
A.单项的系数是 B.单项式的次数为
C.多项式是二次多项式 D.多项式的常数项是7
6.按一定规律排列的单项式:2x,-3x2,4x3,-5x4,6x5,-7x6,…第n个单项式是( )
A. B. C. D.
7.已知a﹣b=2,a﹣c=,则代数式(b﹣c)2+3(b﹣c)+的值是( )
A.﹣ B. C.0 D.
8.下列运算,结果正确的是( )
A.a3+d3=a6 B.2ab﹣ab=2
C.5a2b﹣2ba2=3a2b D.x4﹣x3=x
9.如图,两个正方形的面积分别为16,9,两阴影部分的面积分别为,,则等于( )
A.8 B.7 C.6 D.5
10.如图,点O在直线AB上,点A1,A2,A3,…在射线OA上,点B1,B2,B3,…在射线OB上,图中的每一个实线段和虚线段的长均为1个单位长度.一个动点M从O点出发,按如图所示的箭头方向沿着实线段和以O为圆心的半圆匀速运动,速度为每秒1个单位长度.按此规律,则动点M到达A101点处所需时间为( )秒.
A.5 050π B.5 050π+101 C.5 055π D.5 055π+101
二、填空题(本大题共6个小题,每题3分,共18分)
11.一种商品每件成本为元,现按成本增加20%出售,则这件商品的售价为__________元(用含有的式子表示).
12.若,则代数式的值为________.
13.若a、b互为相反数,c、d互为倒数,m是的相反数,则的值是_________.
14.已知、、在数轴上的位置如图,化简:________.
15.某房间窗户的装饰物如图所示,它由五个半圆组成(半径分别相同),窗户中能射进阳光的部分的面积是______.
16.如图图形都是由同样大小的矩形按一定规律组成,其中第(1)个图形的面积为2cm2,第(2)个图形的面积为8cm2,第(3)个图形的面积为18cm2,…,则第n个图形的面积为_____.
三、解答题(本题共8个小题,共72分;第17-18每小题6分,第19-20每小题8分,第21-22每小题10分,第23-24每小题12分)
17.计算:
(1) (2) (3)
(4) (5) (6)
18.化简并求值:,其中、的取值如图所示.
19.一张边长为x米的正方形铁皮,左边两个角都剪去边长为0.1米的正方形,右边两个角都剪去一边长为0.1米的长方形,如图1所示,将四周折起,做成一个底与盖一样大的长方体铁盒.
(1)请用含x的代数式分别表示铁盒底面长方形的长和宽,并计算长是宽的多少倍?
(2)若x=0.5米,问这个铁盒能否装得下5升(立方分米)液体?请说明理由;
(3)如图2所示,若该铁盒装满了一层高为0.1米的圆柱形易拉罐,求该铁盒空间的利用率(易拉罐总体积与铁盒容积的比).
20.如图,正方形ABCD与正方形BFGE中,点E在边AB上,若AE=a,BE=b,(其中a>2b).
(1)请用含有a,b的代数式表示图中阴影部分的面积;
(2)当a=5cm,b=3cm时,求阴影部分的面积.
21.如图图案是用长度相同的火柴棒按一定规律拼搭而成,图案需8根火柴棒,图案②需15根火柴棒,图案②需15根火柴棒,…
(1)按此规律,图案⑦需____________根火柴棒;
(2)用含n的代数式表示第n个图案需根火柴棒根数.
22.如图,长为60cm,宽为的大长方形被分割为7小块,除阴影A、B外,其余5块是形状大小完全相同的小长方形,其中小长方形的较短一边长度为10cm.
(1)从图可知,每块小长方形的较长的一边长度是_________cm.代数式,中,哪一个代数式的值为正数?_______________.
(2)请你先用含的代数式表示阴影A、B的面积,并说明阴影A的面积一定比阴影B的面积大.
(3)设阴影A和B的面积之和为,阴影A和B的周长之和为,问代数式“S-C”的值可能是负数吗?请你先作出判断,并说明理由.
23.为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的,该市自来水收费标准(按月结算)如表所示:
每月用水量 单价
不超出6的部分 2元/
超出6不超出10的部分 4元/
超出10的部分 8元/
例如:若某户居民1月份用水8,则应收水费:2×6+4×(8﹣6)=20(元).
(1)若该户居民2月份用水12.5,则应收水费 元.
(2)若该户居民3月份用水a(其中6<a<10),则应收水费多少元?(用含a的整式表示,并化简)
(3)若该户居民4月份用水x,4、5两个月共用水15,且5月份用水超过4月份,请用含x的整式表示4、5两个月共交的水费 ,并化简.
24.已知多项式是关于的二次多项式,且二次项系数为,数轴上两点对应的数分别为.
(1)______,______,线段______;
(2)若数轴上有一点,使得,点为的中点,求的长;
(3)有一动点从点出发,以1个单位每秒的速度向终点运动,同时动点从点出发,以个单位每秒的速度在数轴上作同向运动,设运动时间为秒(),点为线段的中点,点为线段的中点,点在线段上且,在的运动过程中,求的值.
答案
一、选择题
C.A.B.B.C.D.C.C.B.B.
二、填空题
11.1.2a.
12.-1
13.4
14.
15.
16.
三、解答题
17.(1)解:原式
;
(2)原式
;
(3)原式
;
(4)原式
;
(5)原式
;
(6)原式
.
18.解:
=
=
=
根据数轴可知,,把,代入得:
原式=.
19.解:
(1) 铁盒底面长方形的长是x-0.1×2=(x-0.2)米,宽是(x-0.1×2)÷2=(0.5x-0.1)米,
(x-0.2)÷(0.5x-0.1)=2.
故长是宽的2倍.
(2) 当x=0.5米时,
(x-0.2)×(0.5x-0.1)×0.1
=(0.5-0.2)×(0.5×0.5-0.1)×0.1
=0.3×0.15×0.1
=0.0045(立方米),
0.0045立方米=4.5升,
4.5升<5升
故这个铁盒不能装得下5升(立方分米)液体.
(3) )[π×(x÷2)2]÷x2=.
故该铁盒空间的利用率是.
20.(1)阴影部分面积的面积=△ABC的面积-△AEG的面积-正方形EBFG的面积-△CFG的面积==;
(2)把a=5,b=3代入上式得:
阴影部分的面积==8(cm2)
答:阴影部分面积是8cm2.
21.(1)解:∵图案①需火柴棒:8根;
图案②需火柴棒:8+7=15根;
图案③需火柴棒:8+7+7=22根;
…
图案⑦需火柴棒:8+7×6=50根;
故答案为:50;
(2)解:由(1)中规律:
图案n需火柴棒:8+7(n-1)=7n+1根;
故答案为:7n+1;
22.(1)解:观察图形可得,小长方形的较长的边为:(厘米),
∴(x-30)为B的较短的一边长,为正数,
故答案为:30;.
(2)解:由图可得,
,
∴阴影A的面积一定比阴影B的面积大.
(3)解:“S-C”的值不可能是负数,理由如下:
由(2)得
,
由图可得
,
∴
,
由图形可得当x最小但不等于30cm时,,
当x最大但不等于40cm时,,
故“S-C”的值不可能是负数.
23.(1)解:应收水费=2×6+4×(10﹣6)+8×(12.5﹣10)=48(元),
故答案为:48;
(2)解:应收水费=不超过6的部分的水费+超出6不超出10部分的水费,
∴应收水费为6×2+4(a﹣6)=(4a﹣12)元,
∴应收水费为(4a﹣12)元;
(3)解:因为5月份用水量超过了4月份,所以4月份用水量少于7.5.
①当4月份用水量少于5时,则5月份用水量超过10,
∴4,5两个月共交水费=2x+8(15﹣x﹣10)+4×4+6×2=(﹣6x+68)元;
②当4月份用水量大于或等于5但不超过6时,则5月份用水量不少于9但不超过10,
∴4、5两个月共交水费=2x+4(15﹣x﹣6)+6×2=(﹣2x+48)元;
③当4月份用水量超过6但少于7.5时,则5月份用水量超过7.5但少于9,
∴4,5两个月共交水费=4(x﹣6)+6×2+4(15﹣x﹣6)+6×2=36(元).
综上所述,当 时,4、5两个月共交的水费为(-6x+68)元;当时,4、5两个月共交的水费为(-2x+48)元;当时,4、5两个月共交的水费为36元.
24.(1).
(2)①当在AB之间时,如图.
若.则.
.
为中点 .
.
②当在延长线上时,如图.
若.则.
.
为中点.
.
.综上或75.
(3)
由题得,对应的数为.对应的数为.
为中点,.
同理,为中点,则.
在上且.且.
对应的数为.
为中点,在上,且.
在右侧.
.
.
.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
