人教版高中数学选择性必修第一册1.4.1用空间向量研究直线、平面的位置关系 精讲精练(含解析)
文档属性
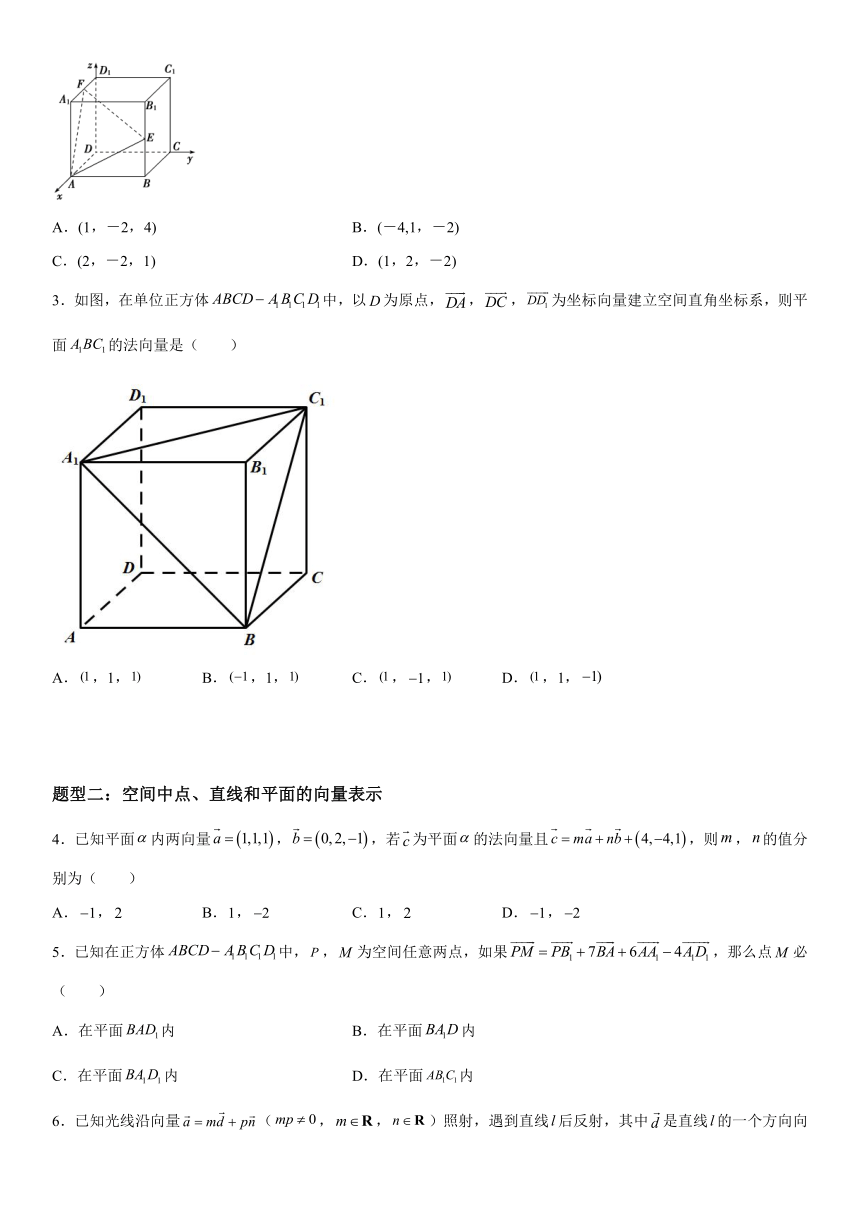
| 名称 | 人教版高中数学选择性必修第一册1.4.1用空间向量研究直线、平面的位置关系 精讲精练(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 00:00:00 | ||
图片预览




文档简介
人教版高中数学选择性必修第一册
1.4.1用空间向量研究直线、平面的位置关系精讲精练同步训练
【考点梳理】
考点一:空间中点、直线和平面的向量表示
1.空间中点的位置向量
如图,在空间中,我们取一定点O作为基点,那么空间中任意一点P就可以用向量来表示.我们把向量称为点P的位置向量.
2.空间中直线的向量表示式
直线l的方向向量为a ,且过点A.如图,取定空间中的任意一点O,可以得到点P在直线l上的充要条件是存在实数t,使
=+ta,①
把=a代入①式得
=+t,②
①式和②式都称为空间直线的向量表示式.
3.空间中平面的向量表示式
平面ABC的向量表示式:空间一点P位于平面ABC内的充要条件是存在实数x,y,使=+x+y.我们称为空间平面ABC的向量表示式.
考点二 空间中平面的法向量
平面的法向量
如图,若直线 l⊥α ,取直线 l 的方向向量a ,我们称a为平面α的法向量;过点A且以 a为法向量的平面完全确定,可以表示为集合 {P|a·=0}.
考点三: 空间中直线、平面的平行
1.线线平行的向量表示
设u1,u2分别是直线l1,l2的方向向量,则
l1∥l2 u1∥u2 λ∈R,使得u1=λu2.
2.线面平行的向量表示
设u是直线 l 的方向向量,n是平面α的法向量,l α,则
l∥α u⊥n u·n=0.
面面平行的向量表示
设n1 ,n2 分别是平面α,β的法向量,则
α∥β n1∥n2 λ∈R,使得n1=λn2 .
考点四:空间中直线、平面的垂直
1.线线垂直的向量表示
设 u1,u2 分别是直线 l1 , l2 的方向向量,则
l1⊥l2 u1⊥u2 u1·u2=0.
2. 线面垂直的向量表示
设u是直线 l 的方向向量,n是平面α的法向量, l α,则l⊥α u∥n λ∈R,使得u=λn.
知识点三 面面垂直的向量表示
设n1,n2 分别是平面α,β的法向量,则
α⊥β n1⊥n2 n1·n2=0.
【题型归纳】
题型一:平面的法向量的求法
1.若直线l的方向向量为(1,0,2),平面的法向量为,则( )
A. B. C.或 D.l与斜交
2.如图,在正方体ABCD 中,以D为原点建立空间直角坐标系,E为B的中点,F为的中点,则下列向量中,能作为平面AEF的法向量的是
A.(1,-2,4) B.(-4,1,-2)
C.(2,-2,1) D.(1,2,-2)
3.如图,在单位正方体中,以为原点,,,为坐标向量建立空间直角坐标系,则平面的法向量是( )
A.,1, B.,1, C.,, D.,1,
题型二:空间中点、直线和平面的向量表示
4.已知平面内两向量,,若为平面的法向量且,则,的值分别为( )
A., B., C., D.,
5.已知在正方体中,,为空间任意两点,如果,那么点必( )
A.在平面内 B.在平面内
C.在平面内 D.在平面内
6.已知光线沿向量(,,)照射,遇到直线后反射,其中是直线的一个方向向量,是直线的一个法向量,则反射光线的方向向量一定可以表示为
A. B.
C. D.
题型三:空间中直线、平面的平行
7.已知=(2,4,5),=(3,x,y)分别是直线l1、l2的方向向量.若l1∥l2,则( )
A.x=6,y=15 B.x=3,y=
C.x=3,y=15 D.x=6,y=
8.设平面的一个法向量为=(1,2,-2),平面的一个法向量为=(-2,-4,k),若,则k=( )
A.-5 B.-4 C.-2 D.4
9.如图,在正方体AC1中,PQ与直线A1D和AC都垂直,则直线PQ与BD1的关系是( )
A.异面直线
B.平行直线
C.垂直不相交
D.垂直且相交
题型四:空间中直线、平面的垂直
10.已知平面α的法向量为=(1,2,-2),平面β的法向量为=(-2,-4,k),若α⊥β,则k等于( )
A.4 B.-4 C.5 D.-5
11.已知两不重合直线l1和l2的方向向量分别为a=(3λ+1,0,2λ),b=(1,λ-1,λ),若l1⊥l2,则λ的值为( )
A.1或- B.1或
C.-1或 D.-1或-
12.在四棱锥P-ABCD中,底面ABCD是平行四边形,,,则PA与底面ABCD的关系是( )
A.相交 B.垂直
C.不垂直 D.成60°角
【双基达标】
一、单选题
13.若直线的方向向量为,平面的法向量为,则( ).
A. B. C. D.与相交
14.已知向量是平面α的两个不相等的非零向量,非零向量是直线的一个方向向量,则且是l⊥α的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
15.若直线l的方向向量为,平面α的法向量为,则能使l∥α的是( )
A., B.,
C., D.,
16.直线的方向向量,平面α的法向量为,若直线平面,则实数的值为( )
A. B. C. D.
17.已知正方体,是棱的中点,则在棱上存在点,使得( )
A. B.
C.平面 D.平面
18.平面的一个法向量是,,,平面的一个法向量是,6,,则平面与平面的关系是( )
A.平行 B.重合 C.平行或重合 D.垂直
19.如图所示,在正方体ABCD-A1B1C1D1中,棱长为a,M,N分别为A1B和AC上的点,A1M=AN=,则MN与平面BB1C1C的位置关系是( )
A.相交 B.平行
C.垂直 D.MN在平面BB1C1C内
20.下列命题中,正确命题的个数为( )
①若分别是平面α,β的法向量,则 α∥β;
②若分别是平面α,β的法向量,则α⊥β ;
③若是平面α的法向量,是直线l的方向向量,若l与平面α平行,则;
④若两个平面的法向量不垂直,则这两个平面不垂直.
A.1 B.2 C.3 D.4
21.如图,在正方体中,点,,分别是线段,,的中点,则直线与,的位置关系是( )
A.与,均垂直
B.与垂直,与不垂直
C.与不垂直,与垂直
D.与,均不垂直
22.如图所示,正方体中,分别在上,且,则( )
A.至多与之一垂直 B.
C.与相交 D.与异面
【高分突破】
一:单选题
23.已知向量 , ,分别是直线 、 的方向向量,若 ,则
A. , B. , C. , D. ,
24.已知A,B,C三点不共线,对于平面ABC外的任一点O,下列条件中能确定点M与点A,B,C一定共面的是
A. B.
C. D.
25.已知向量,平面的一个法向量,若,则
A., B., C. D.
26.已知为直线l的方向向量,,分别为平面,的法向量不重合那么下列说法中:
;;;正确的有
A.1个 B.2个 C.3个 D.4个
27.在如图所示的坐标系中,为正方体,给出下列结论:
①直线 的一个方向向量为(0,0,1);
②直线的一个方向向量为(0,1,1);
③平面的一个法向量为(0,1,0);
④平面的一个法向量为(1,1,1).
其中正确的个数为( )
A.1 B.2 C.3 D.4
28.设空间四点O、A、B、P满足=m+n,其中m+n=1,则
A.点P一定在直线AB上
B.点P一定不在直线AB上
C.点P不一定在直线AB上
D.以上都不对
29.在三棱锥中,、、两两垂直,,,如图,建立空间直角坐标系,则下列向量中是平面的法向量的是( )
A. B.
C. D.
30.如图,正方形ABCD与矩形ACEF所在平面互相垂直,AB=,AF=1,M在EF上,且AM∥平面BDE.则M点的坐标为( )
A.(1,1,1) B. C. D.
二、多选题
31.如图,一个结晶体的形状为平行六面体,其中,以顶点A为端点的三条棱长都相等,且它们彼此的夹角都是60°,下列说法中正确的是( )
A. B.
C.向量与的夹角是60° D.与AC所成角的余弦值为
32.如图,正方体的棱长为1,是的中点,则( )
A.直线平面 B.
C.三棱锥的体积为 D.异面直线与所成的角为
33.(多选)下列命题是真命题的有( ).
A.直线的方向向量为,直线的方向向量为,则与垂直
B.直线的方向向量为,平面的法向量为,则
C.平面,的法向量分别为,,则
D.平面经过三点,,,向量是平面的法向量,则
34.已知空间中三点,,,则下列说法正确的是( )
A.与是共线向量 B.与同向的单位向量是
C.和夹角的余弦值是 D.平面的一个法向量是
35.已知点P是平行四边形ABCD所在的平面外一点,如果,,,下列结论正确的有( )
A. B.
C.是平面ABCD的一个法向量 D.
36.已知矩形,,,将沿矩形的对角线所在的直线进行翻折,翻折过程中( )
A.存在某个位置,使得
B.存在某个位置,使得
C.存在某个位置,使得
D.存在某个位置,使得,、均不等于零
三、填空题
37.已知平面α经过点O(0,0,0),且=(1,2,-3)是α的一个法向量,M(x,y,z)是平面α内任意一点,则x,y,z满足的关系式是________________.
38.已知α,β为两个不重合的平面,设平面与向量=(-1,2,-4)垂直,平面β与向量=(-2,4,-8)垂直,则平面与β的位置关系是________.
39.若=是平面α的一个法向量,且=(-1,2,1),=均与平面α平行,则向量=________.
40.如图,在长方体ABCD-A1B1C1D1中,,P为C1D1的中点,M为BC的中点,则AM与PM的位置关系是________.
41.在△ABC中,A(1,-2,-1),B(0,-3,1),C(2,-2,1).若向量与平面ABC垂直,且,则的坐标为________________.
42.在如图所示的坐标系中,ABCD-A1B1C1D1表示棱长为1的正方体,给出下列结论:
①直线DD1的一个方向向量为(0,0,1);②直线BC1的一个方向向量为(0,1,1);③平面ABB1A1的一个法向量为(0,1,0);④平面B1CD的一个法向量为(1,1,1).
其中正确的是________.(填序号)
四、解答题
43.如图,已知P是平面四边形ABCD所在平面外一点,连接PA PB PD.点E F G H分别为PAB PBC PCD PDA的重心.,求证:
(1)E F G H四点共面;
(2)平面EFGH平面ABCD.
44.如图,在等腰梯形中,,,,平面,,且,,Q分别是线段,AB的中点.
(1)求证:平面平面;
(2)求证:PQ平面.
45.如图,在四面体ABOC中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=1,设P为AC的中点,Q在AB上且AB=3AQ,证明:PQ⊥OA.
46.如图,在底面是矩形的四棱锥中,底面,、分别是、的中点,,.求证:
(1)平面;
(2)平面平面.
47.如图所示,平面CDEF平面ABCD,且四边形ABCD为平行四边形,∠DAB=45°,四边形CDEF为直角梯形,EF∥DC,EDCD,AB=3EF=3,ED=a,AD.
(1)求证:ADBF;
(2)若线段CF上存在一点M,满足AE∥平面BDM,求的值;
【答案详解】
1.C
∵ ,,
∴ ,即或.
故选:C.
2.B
设正方体棱长为2,则A(2,0,0),E(2,2,1),F(1,0,2),
∴=(0,2,1),=(﹣1,0,2)
设向量=(x,y,z)是平面AEF的一个法向量
则,取y=1,得x=﹣4,z=﹣2
∴=(﹣4,1,﹣2)是平面AEF的一个法向量
因此可得:只有B选项的向量是平面AEF的法向量
故选B.
3.A
在单位正方体中,
以为原点,,,为坐标向量建立空间直角坐标系,
,0,,,1,,,1,,
,1,,,0,,
设平面的法向量是,,,
则,取,得,1,,
平面的法向量是,1,.
故选:.
4.A
因为,,
所以
,
因为为平面的法向量,
所以,即,
解得:,所以,的值分别为,,
故选:A.
5.C
因为
,所以,,,四点共面
6.B
不妨设入射光线与反射光线的方向向量模相等,即如图中,则向量时,向量.故选B.
7.D
由l1∥l2得,,解得x=6,y=.
8.D
因为,所以,则 ,解之得,
故选:D
9.B
设正方体的棱长为1,取D点为坐标原点建系后如图所示:
则,,, ,,
=(1,0,1),=(-1,1,0),
设=(a,b,c),
则
取=(1,1,-1),
∵=(0,0,1)-(1,1,0)=(-1,-1,1)=-,
∴∥,
∴PQ∥BD1.
故选:B
10.D
解:由平面α的法向量为,平面β的法向量为,
∵α⊥β,∴,
∴.
∴.
故选:D.
11.D
【详解】
由题意知,a⊥b,
∴3λ+1+2λ2=0,
∴λ=-1或-.
12.B
解:因为,所以;
因为,所以,
又,
所以平面ABCD.
故选:B.
13.B
,
由已知可得,则,因此,.
故选:B.
14.B
【详解】
当不共线时,由且,可推出l⊥α;当为共线向量时,由且,不能够推出,所以且是l⊥α的不充分条件;
若,则一定有且,所以且是l⊥α的必要条件.
故选:.
15.D
【详解】
由题意得,若使l∥α,那么就要使,即.
对于A,,故A错误;
对于B,,故B错误;
对于C,,故C错误;
对于D,,故D正确.
故选:D.
16.D
因为直线的方向向量,平面α的法向量为,
直线平面,
所以,即,解得:
故选:D.
17.B
建立如图所示的空间直角坐标系,设正方体棱长为1,则,,,设(,
则,,
因为,所以不可能平行,即不可能平行,
又,,因此可以垂直,即与可能垂直.
,,
设平面的一个法向量为,
则,取,则,
与不可能平行,因此与平面不可能垂直,
,因此与不可能垂直,因此与平面不可能平行,
故选:B.
18.C
平面的一个法向量是,,,平面的一个法向量是,6,,
,
平面与平面的关系是平行或重合.
故选:C.
19.B
以点C1为坐标原点,分别以C1B1,C1D1,C1C所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
由于A1M=AN=,则
又C1D1⊥平面BB1C1C,所以=(0,a,0)为平面BB1C1C的一个法向量.
因为,所以,又平面BB1C1C,所以MN∥平面BB1C1C.
故选:B
20.C
①中平面α,β可能平行,也可能重合,结合平面法向量的概念,可知②③④正确
故选:C
21.A
如图,以D为原点,建立空间直角坐标系,设正方体的棱长为,则,,,,,
则,,
,即
,即
所以直线与,均垂直,
故选:A
22.B
如图,以为坐标原点,分别以,,所在直线为轴、轴、轴建立空间直角坐标系.
设正方体的棱长为3,则,,,,,,,.
,,,
,,,,∴A错误,B正确;
,,,
,即,∴C,D错误.
故选:B.
23.D
【详解】
∵∥,
∴ ∥ ,
∴,
∴.选D.
24.D
设,若点与点共面,,则,只有选项D满足,.故选D.
25.A
因为,所以,由,得,.
故选A
【点睛】
本题考查了空间法向量的定义,空间向量共线的坐标表示,属于基础题.
26.B
∵平面,不重合;
平面,的法向量平行垂直等价于平面,平行垂直;
正确;
直线l的方向向量平行垂直于平面的法向量等价于直线l垂直平行于平面;
都错误.
故选B.
27.C
DD1∥AA1,=(0,0,1),故①正确;
BC1∥AD1,=(0,1,1), 故②正确;
直线AD⊥平面ABB1A1,=(0,1,0). 故③正确;
点C1的坐标为(1,1,1),与平面B1CD不垂直,故④错.
28.A
由可得:,结合题意可知:
,
即:,,
据此可知:APB三点共线,点P一定在直线AB上.
29.A
,,设平面的一个法向量为,
由则,解得,.
又,因此,平面的一个法向量为.
故选:A.
30.C
设交于点,连结,因为正方形与矩形所在的平面互相垂直,,点在上,且平面,所以,又,所以是平行四边形,所以是的中点,因为,所以,故选C.
31.AB
以顶点A为端点的三条棱长都相等, 它们彼此的夹角都是60°,
可设棱长为1,则
而
, 所以A正确.
=0,所以B正确.
向量,
显然 为等边三角形,则.
所以向量与的夹角是 ,向量与的夹角是,则C不正确
又,
则,
所以,所以D不正确.
故选:AB
32.ABD
解:如图建立空间直角坐标系,,,,,,,,,,
,,,
所以,即,所以,故B正确;
,,,
设异面直线与所成的角为,则,又,所以,故D正确;
设平面的法向量为,则,即,取,
则,即,又直线平面,所以直线平面,故A正确;
,故C错误;
故选:ABD
33.AD
∵,,
∴,则,
∴直线与垂直,故A正确;
,,则,
则,∴或,故B错误;
∵,,∴与不共线,
∴不成立,故C错误;
∵点,,,
∴,.
∵向量是平面的法向量,∴,
即,解得,故D正确.
故选:AD
34.BD
对于A,,,可知,与不共线,A错误;
对于B,,,,即与同向的单位向量是,B正确;
对于C,,,
即和夹角的余弦值为,C错误;
对于D,设平面的法向量,
则,令,解得:,,,
即平面的一个法向量为,D正确.
故选:BD.
35.ABC
因为,所以,A正确;
因为,所以,B正确;
由,,可得是平面ABCD的一个法向量,C正确;
BD在平面ABCD内,可得,D错误.
故选:ABC.
36.AD
在矩形中,分别过点、作、,垂足分别为点、.
由已知条件,,.
对于A选项,若存在某个位置,使得,
,,平面,平面,则,
在中,斜边,存在,故A正确;
对于B选项,若存在某个位置,使得,
,,平面,平面,则,
在中,斜边,矛盾,故B错误;
对于C选项,若存在某个位置,使得,
,,平面,平面,,
,在平面内,过点能作两条直线与垂直,矛盾,故C错误;
对于D选项,取平面平面,
,平面平面,平面,平面,
以点为坐标原点,、所在直线分别为、轴建立如下图所示的空间直角坐标系,
则、、、,
,,则,
,,则,
,,则,D选项正确.
故选:AD.
37.x+2y-3z=0
解:由题意得⊥,,
则,
所以x,y,z满足的关系式是x+2y-3z=0.
故答案为:x+2y-3z=0.
38.平行
,,,
所以,又分别是平面的法向量,
所以.
故答案为:平行
39.
解析 由题意,知
即解得
所以.
故答案为:
40.PM⊥AM
【详解】
解:以点为原点,、、为轴、轴、轴正方向,建立如图所示的空间直角坐标系
可得,.
,,
由此可得,
即,可得.
故答案为:
41.(-2,4,1)或(2,-4,-1)
【详解】
据题意,得=(-1,-1,2),=(1,0,2).
设(x,y,z),∵与平面ABC垂直,
即 可得
,,
解得或.
当时,,;当时,,.
∴的坐标为(-2,4,1)或(2,-4,-1).
故答案为:(-2,4,1)或(2,-4,-1)
42.①②③
解析 ==(0,0,1),故①正确;==(0,1,1),故②正确;直线AD⊥平面ABB1A1,=(0,1,0),故③正确;向量的坐标为(1,1,1),与平面B1CD不垂直,∴④错.
43.
(1)∵E F G H分别是所在三角形的重心.
∴M、N、Q、R为所在边的中点,顺次连接M、N、Q、R所得四边形为平行四边形,
且有,,,.
∵四边形MNQR为平行四边形,
则
.
∴由共面向量定理得E F G H四点共面;
(2)由(1)知,∴MQEG,
由平面ABCD,平面ABCD,从而EG平面ABCD,
又,∴MNEF,
由平面ABCD,平面ABCD,从而EF平面ABCD,
又∵EG∩EF=E,平面EFGH,
∴平面EFGH平面ABCD.
44.
(1)平面,平面,则,在中,由余弦定理:,在中,由正弦定理:
,解得,又,则,于是,即,又,故平面,又平面,则平面平面.
(2)由第一问知,是平面的法向量,于是只要证明即可,即证,由向量的运算:,,两式相加得:,于是,
即,显然点平面,点平面,则直线平面,于是PQ平面.
45.
,
.
∴PQ⊥OA.
46.
以为原点,所在直线为轴,所在直线为轴,所在直线为轴,建立如图所示的空间直角坐标系,
则、、、、,所以、,
,,,,,,.
(1)因为,所以,即.
又平面,平面,所以平面;
(2)因为,所以,同理可得,
即,.
又,所以平面.
平面,所以平面平面.
47.
(1)∵面CDEF面ABCD,EDCD,面,面面,
∴ED面ABCD,面,即,
过作于,过作交于,
∵CDEF为直角梯形,AB=3EF=3,
∴,即,则,且,
∴,得,即,
∴,而,即面,又面,
∴,故.
(2)以D为原点,过点D垂直于DC的直线为x轴,DC所在直线为y轴,所在直线为z轴,建立空间直角坐标系,如下图示:
∴,若,则,
设,则,
设平面BDM的法向量为,则,取x1=2,则,
若AE∥平面BDM,则,解得,
∴线段CF上存在一点M,满足AE∥平面BDM,此时.
试卷第1页,总3页
1.4.1用空间向量研究直线、平面的位置关系精讲精练同步训练
【考点梳理】
考点一:空间中点、直线和平面的向量表示
1.空间中点的位置向量
如图,在空间中,我们取一定点O作为基点,那么空间中任意一点P就可以用向量来表示.我们把向量称为点P的位置向量.
2.空间中直线的向量表示式
直线l的方向向量为a ,且过点A.如图,取定空间中的任意一点O,可以得到点P在直线l上的充要条件是存在实数t,使
=+ta,①
把=a代入①式得
=+t,②
①式和②式都称为空间直线的向量表示式.
3.空间中平面的向量表示式
平面ABC的向量表示式:空间一点P位于平面ABC内的充要条件是存在实数x,y,使=+x+y.我们称为空间平面ABC的向量表示式.
考点二 空间中平面的法向量
平面的法向量
如图,若直线 l⊥α ,取直线 l 的方向向量a ,我们称a为平面α的法向量;过点A且以 a为法向量的平面完全确定,可以表示为集合 {P|a·=0}.
考点三: 空间中直线、平面的平行
1.线线平行的向量表示
设u1,u2分别是直线l1,l2的方向向量,则
l1∥l2 u1∥u2 λ∈R,使得u1=λu2.
2.线面平行的向量表示
设u是直线 l 的方向向量,n是平面α的法向量,l α,则
l∥α u⊥n u·n=0.
面面平行的向量表示
设n1 ,n2 分别是平面α,β的法向量,则
α∥β n1∥n2 λ∈R,使得n1=λn2 .
考点四:空间中直线、平面的垂直
1.线线垂直的向量表示
设 u1,u2 分别是直线 l1 , l2 的方向向量,则
l1⊥l2 u1⊥u2 u1·u2=0.
2. 线面垂直的向量表示
设u是直线 l 的方向向量,n是平面α的法向量, l α,则l⊥α u∥n λ∈R,使得u=λn.
知识点三 面面垂直的向量表示
设n1,n2 分别是平面α,β的法向量,则
α⊥β n1⊥n2 n1·n2=0.
【题型归纳】
题型一:平面的法向量的求法
1.若直线l的方向向量为(1,0,2),平面的法向量为,则( )
A. B. C.或 D.l与斜交
2.如图,在正方体ABCD 中,以D为原点建立空间直角坐标系,E为B的中点,F为的中点,则下列向量中,能作为平面AEF的法向量的是
A.(1,-2,4) B.(-4,1,-2)
C.(2,-2,1) D.(1,2,-2)
3.如图,在单位正方体中,以为原点,,,为坐标向量建立空间直角坐标系,则平面的法向量是( )
A.,1, B.,1, C.,, D.,1,
题型二:空间中点、直线和平面的向量表示
4.已知平面内两向量,,若为平面的法向量且,则,的值分别为( )
A., B., C., D.,
5.已知在正方体中,,为空间任意两点,如果,那么点必( )
A.在平面内 B.在平面内
C.在平面内 D.在平面内
6.已知光线沿向量(,,)照射,遇到直线后反射,其中是直线的一个方向向量,是直线的一个法向量,则反射光线的方向向量一定可以表示为
A. B.
C. D.
题型三:空间中直线、平面的平行
7.已知=(2,4,5),=(3,x,y)分别是直线l1、l2的方向向量.若l1∥l2,则( )
A.x=6,y=15 B.x=3,y=
C.x=3,y=15 D.x=6,y=
8.设平面的一个法向量为=(1,2,-2),平面的一个法向量为=(-2,-4,k),若,则k=( )
A.-5 B.-4 C.-2 D.4
9.如图,在正方体AC1中,PQ与直线A1D和AC都垂直,则直线PQ与BD1的关系是( )
A.异面直线
B.平行直线
C.垂直不相交
D.垂直且相交
题型四:空间中直线、平面的垂直
10.已知平面α的法向量为=(1,2,-2),平面β的法向量为=(-2,-4,k),若α⊥β,则k等于( )
A.4 B.-4 C.5 D.-5
11.已知两不重合直线l1和l2的方向向量分别为a=(3λ+1,0,2λ),b=(1,λ-1,λ),若l1⊥l2,则λ的值为( )
A.1或- B.1或
C.-1或 D.-1或-
12.在四棱锥P-ABCD中,底面ABCD是平行四边形,,,则PA与底面ABCD的关系是( )
A.相交 B.垂直
C.不垂直 D.成60°角
【双基达标】
一、单选题
13.若直线的方向向量为,平面的法向量为,则( ).
A. B. C. D.与相交
14.已知向量是平面α的两个不相等的非零向量,非零向量是直线的一个方向向量,则且是l⊥α的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
15.若直线l的方向向量为,平面α的法向量为,则能使l∥α的是( )
A., B.,
C., D.,
16.直线的方向向量,平面α的法向量为,若直线平面,则实数的值为( )
A. B. C. D.
17.已知正方体,是棱的中点,则在棱上存在点,使得( )
A. B.
C.平面 D.平面
18.平面的一个法向量是,,,平面的一个法向量是,6,,则平面与平面的关系是( )
A.平行 B.重合 C.平行或重合 D.垂直
19.如图所示,在正方体ABCD-A1B1C1D1中,棱长为a,M,N分别为A1B和AC上的点,A1M=AN=,则MN与平面BB1C1C的位置关系是( )
A.相交 B.平行
C.垂直 D.MN在平面BB1C1C内
20.下列命题中,正确命题的个数为( )
①若分别是平面α,β的法向量,则 α∥β;
②若分别是平面α,β的法向量,则α⊥β ;
③若是平面α的法向量,是直线l的方向向量,若l与平面α平行,则;
④若两个平面的法向量不垂直,则这两个平面不垂直.
A.1 B.2 C.3 D.4
21.如图,在正方体中,点,,分别是线段,,的中点,则直线与,的位置关系是( )
A.与,均垂直
B.与垂直,与不垂直
C.与不垂直,与垂直
D.与,均不垂直
22.如图所示,正方体中,分别在上,且,则( )
A.至多与之一垂直 B.
C.与相交 D.与异面
【高分突破】
一:单选题
23.已知向量 , ,分别是直线 、 的方向向量,若 ,则
A. , B. , C. , D. ,
24.已知A,B,C三点不共线,对于平面ABC外的任一点O,下列条件中能确定点M与点A,B,C一定共面的是
A. B.
C. D.
25.已知向量,平面的一个法向量,若,则
A., B., C. D.
26.已知为直线l的方向向量,,分别为平面,的法向量不重合那么下列说法中:
;;;正确的有
A.1个 B.2个 C.3个 D.4个
27.在如图所示的坐标系中,为正方体,给出下列结论:
①直线 的一个方向向量为(0,0,1);
②直线的一个方向向量为(0,1,1);
③平面的一个法向量为(0,1,0);
④平面的一个法向量为(1,1,1).
其中正确的个数为( )
A.1 B.2 C.3 D.4
28.设空间四点O、A、B、P满足=m+n,其中m+n=1,则
A.点P一定在直线AB上
B.点P一定不在直线AB上
C.点P不一定在直线AB上
D.以上都不对
29.在三棱锥中,、、两两垂直,,,如图,建立空间直角坐标系,则下列向量中是平面的法向量的是( )
A. B.
C. D.
30.如图,正方形ABCD与矩形ACEF所在平面互相垂直,AB=,AF=1,M在EF上,且AM∥平面BDE.则M点的坐标为( )
A.(1,1,1) B. C. D.
二、多选题
31.如图,一个结晶体的形状为平行六面体,其中,以顶点A为端点的三条棱长都相等,且它们彼此的夹角都是60°,下列说法中正确的是( )
A. B.
C.向量与的夹角是60° D.与AC所成角的余弦值为
32.如图,正方体的棱长为1,是的中点,则( )
A.直线平面 B.
C.三棱锥的体积为 D.异面直线与所成的角为
33.(多选)下列命题是真命题的有( ).
A.直线的方向向量为,直线的方向向量为,则与垂直
B.直线的方向向量为,平面的法向量为,则
C.平面,的法向量分别为,,则
D.平面经过三点,,,向量是平面的法向量,则
34.已知空间中三点,,,则下列说法正确的是( )
A.与是共线向量 B.与同向的单位向量是
C.和夹角的余弦值是 D.平面的一个法向量是
35.已知点P是平行四边形ABCD所在的平面外一点,如果,,,下列结论正确的有( )
A. B.
C.是平面ABCD的一个法向量 D.
36.已知矩形,,,将沿矩形的对角线所在的直线进行翻折,翻折过程中( )
A.存在某个位置,使得
B.存在某个位置,使得
C.存在某个位置,使得
D.存在某个位置,使得,、均不等于零
三、填空题
37.已知平面α经过点O(0,0,0),且=(1,2,-3)是α的一个法向量,M(x,y,z)是平面α内任意一点,则x,y,z满足的关系式是________________.
38.已知α,β为两个不重合的平面,设平面与向量=(-1,2,-4)垂直,平面β与向量=(-2,4,-8)垂直,则平面与β的位置关系是________.
39.若=是平面α的一个法向量,且=(-1,2,1),=均与平面α平行,则向量=________.
40.如图,在长方体ABCD-A1B1C1D1中,,P为C1D1的中点,M为BC的中点,则AM与PM的位置关系是________.
41.在△ABC中,A(1,-2,-1),B(0,-3,1),C(2,-2,1).若向量与平面ABC垂直,且,则的坐标为________________.
42.在如图所示的坐标系中,ABCD-A1B1C1D1表示棱长为1的正方体,给出下列结论:
①直线DD1的一个方向向量为(0,0,1);②直线BC1的一个方向向量为(0,1,1);③平面ABB1A1的一个法向量为(0,1,0);④平面B1CD的一个法向量为(1,1,1).
其中正确的是________.(填序号)
四、解答题
43.如图,已知P是平面四边形ABCD所在平面外一点,连接PA PB PD.点E F G H分别为PAB PBC PCD PDA的重心.,求证:
(1)E F G H四点共面;
(2)平面EFGH平面ABCD.
44.如图,在等腰梯形中,,,,平面,,且,,Q分别是线段,AB的中点.
(1)求证:平面平面;
(2)求证:PQ平面.
45.如图,在四面体ABOC中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=1,设P为AC的中点,Q在AB上且AB=3AQ,证明:PQ⊥OA.
46.如图,在底面是矩形的四棱锥中,底面,、分别是、的中点,,.求证:
(1)平面;
(2)平面平面.
47.如图所示,平面CDEF平面ABCD,且四边形ABCD为平行四边形,∠DAB=45°,四边形CDEF为直角梯形,EF∥DC,EDCD,AB=3EF=3,ED=a,AD.
(1)求证:ADBF;
(2)若线段CF上存在一点M,满足AE∥平面BDM,求的值;
【答案详解】
1.C
∵ ,,
∴ ,即或.
故选:C.
2.B
设正方体棱长为2,则A(2,0,0),E(2,2,1),F(1,0,2),
∴=(0,2,1),=(﹣1,0,2)
设向量=(x,y,z)是平面AEF的一个法向量
则,取y=1,得x=﹣4,z=﹣2
∴=(﹣4,1,﹣2)是平面AEF的一个法向量
因此可得:只有B选项的向量是平面AEF的法向量
故选B.
3.A
在单位正方体中,
以为原点,,,为坐标向量建立空间直角坐标系,
,0,,,1,,,1,,
,1,,,0,,
设平面的法向量是,,,
则,取,得,1,,
平面的法向量是,1,.
故选:.
4.A
因为,,
所以
,
因为为平面的法向量,
所以,即,
解得:,所以,的值分别为,,
故选:A.
5.C
因为
,所以,,,四点共面
6.B
不妨设入射光线与反射光线的方向向量模相等,即如图中,则向量时,向量.故选B.
7.D
由l1∥l2得,,解得x=6,y=.
8.D
因为,所以,则 ,解之得,
故选:D
9.B
设正方体的棱长为1,取D点为坐标原点建系后如图所示:
则,,, ,,
=(1,0,1),=(-1,1,0),
设=(a,b,c),
则
取=(1,1,-1),
∵=(0,0,1)-(1,1,0)=(-1,-1,1)=-,
∴∥,
∴PQ∥BD1.
故选:B
10.D
解:由平面α的法向量为,平面β的法向量为,
∵α⊥β,∴,
∴.
∴.
故选:D.
11.D
【详解】
由题意知,a⊥b,
∴3λ+1+2λ2=0,
∴λ=-1或-.
12.B
解:因为,所以;
因为,所以,
又,
所以平面ABCD.
故选:B.
13.B
,
由已知可得,则,因此,.
故选:B.
14.B
【详解】
当不共线时,由且,可推出l⊥α;当为共线向量时,由且,不能够推出,所以且是l⊥α的不充分条件;
若,则一定有且,所以且是l⊥α的必要条件.
故选:.
15.D
【详解】
由题意得,若使l∥α,那么就要使,即.
对于A,,故A错误;
对于B,,故B错误;
对于C,,故C错误;
对于D,,故D正确.
故选:D.
16.D
因为直线的方向向量,平面α的法向量为,
直线平面,
所以,即,解得:
故选:D.
17.B
建立如图所示的空间直角坐标系,设正方体棱长为1,则,,,设(,
则,,
因为,所以不可能平行,即不可能平行,
又,,因此可以垂直,即与可能垂直.
,,
设平面的一个法向量为,
则,取,则,
与不可能平行,因此与平面不可能垂直,
,因此与不可能垂直,因此与平面不可能平行,
故选:B.
18.C
平面的一个法向量是,,,平面的一个法向量是,6,,
,
平面与平面的关系是平行或重合.
故选:C.
19.B
以点C1为坐标原点,分别以C1B1,C1D1,C1C所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
由于A1M=AN=,则
又C1D1⊥平面BB1C1C,所以=(0,a,0)为平面BB1C1C的一个法向量.
因为,所以,又平面BB1C1C,所以MN∥平面BB1C1C.
故选:B
20.C
①中平面α,β可能平行,也可能重合,结合平面法向量的概念,可知②③④正确
故选:C
21.A
如图,以D为原点,建立空间直角坐标系,设正方体的棱长为,则,,,,,
则,,
,即
,即
所以直线与,均垂直,
故选:A
22.B
如图,以为坐标原点,分别以,,所在直线为轴、轴、轴建立空间直角坐标系.
设正方体的棱长为3,则,,,,,,,.
,,,
,,,,∴A错误,B正确;
,,,
,即,∴C,D错误.
故选:B.
23.D
【详解】
∵∥,
∴ ∥ ,
∴,
∴.选D.
24.D
设,若点与点共面,,则,只有选项D满足,.故选D.
25.A
因为,所以,由,得,.
故选A
【点睛】
本题考查了空间法向量的定义,空间向量共线的坐标表示,属于基础题.
26.B
∵平面,不重合;
平面,的法向量平行垂直等价于平面,平行垂直;
正确;
直线l的方向向量平行垂直于平面的法向量等价于直线l垂直平行于平面;
都错误.
故选B.
27.C
DD1∥AA1,=(0,0,1),故①正确;
BC1∥AD1,=(0,1,1), 故②正确;
直线AD⊥平面ABB1A1,=(0,1,0). 故③正确;
点C1的坐标为(1,1,1),与平面B1CD不垂直,故④错.
28.A
由可得:,结合题意可知:
,
即:,,
据此可知:APB三点共线,点P一定在直线AB上.
29.A
,,设平面的一个法向量为,
由则,解得,.
又,因此,平面的一个法向量为.
故选:A.
30.C
设交于点,连结,因为正方形与矩形所在的平面互相垂直,,点在上,且平面,所以,又,所以是平行四边形,所以是的中点,因为,所以,故选C.
31.AB
以顶点A为端点的三条棱长都相等, 它们彼此的夹角都是60°,
可设棱长为1,则
而
, 所以A正确.
=0,所以B正确.
向量,
显然 为等边三角形,则.
所以向量与的夹角是 ,向量与的夹角是,则C不正确
又,
则,
所以,所以D不正确.
故选:AB
32.ABD
解:如图建立空间直角坐标系,,,,,,,,,,
,,,
所以,即,所以,故B正确;
,,,
设异面直线与所成的角为,则,又,所以,故D正确;
设平面的法向量为,则,即,取,
则,即,又直线平面,所以直线平面,故A正确;
,故C错误;
故选:ABD
33.AD
∵,,
∴,则,
∴直线与垂直,故A正确;
,,则,
则,∴或,故B错误;
∵,,∴与不共线,
∴不成立,故C错误;
∵点,,,
∴,.
∵向量是平面的法向量,∴,
即,解得,故D正确.
故选:AD
34.BD
对于A,,,可知,与不共线,A错误;
对于B,,,,即与同向的单位向量是,B正确;
对于C,,,
即和夹角的余弦值为,C错误;
对于D,设平面的法向量,
则,令,解得:,,,
即平面的一个法向量为,D正确.
故选:BD.
35.ABC
因为,所以,A正确;
因为,所以,B正确;
由,,可得是平面ABCD的一个法向量,C正确;
BD在平面ABCD内,可得,D错误.
故选:ABC.
36.AD
在矩形中,分别过点、作、,垂足分别为点、.
由已知条件,,.
对于A选项,若存在某个位置,使得,
,,平面,平面,则,
在中,斜边,存在,故A正确;
对于B选项,若存在某个位置,使得,
,,平面,平面,则,
在中,斜边,矛盾,故B错误;
对于C选项,若存在某个位置,使得,
,,平面,平面,,
,在平面内,过点能作两条直线与垂直,矛盾,故C错误;
对于D选项,取平面平面,
,平面平面,平面,平面,
以点为坐标原点,、所在直线分别为、轴建立如下图所示的空间直角坐标系,
则、、、,
,,则,
,,则,
,,则,D选项正确.
故选:AD.
37.x+2y-3z=0
解:由题意得⊥,,
则,
所以x,y,z满足的关系式是x+2y-3z=0.
故答案为:x+2y-3z=0.
38.平行
,,,
所以,又分别是平面的法向量,
所以.
故答案为:平行
39.
解析 由题意,知
即解得
所以.
故答案为:
40.PM⊥AM
【详解】
解:以点为原点,、、为轴、轴、轴正方向,建立如图所示的空间直角坐标系
可得,.
,,
由此可得,
即,可得.
故答案为:
41.(-2,4,1)或(2,-4,-1)
【详解】
据题意,得=(-1,-1,2),=(1,0,2).
设(x,y,z),∵与平面ABC垂直,
即 可得
,,
解得或.
当时,,;当时,,.
∴的坐标为(-2,4,1)或(2,-4,-1).
故答案为:(-2,4,1)或(2,-4,-1)
42.①②③
解析 ==(0,0,1),故①正确;==(0,1,1),故②正确;直线AD⊥平面ABB1A1,=(0,1,0),故③正确;向量的坐标为(1,1,1),与平面B1CD不垂直,∴④错.
43.
(1)∵E F G H分别是所在三角形的重心.
∴M、N、Q、R为所在边的中点,顺次连接M、N、Q、R所得四边形为平行四边形,
且有,,,.
∵四边形MNQR为平行四边形,
则
.
∴由共面向量定理得E F G H四点共面;
(2)由(1)知,∴MQEG,
由平面ABCD,平面ABCD,从而EG平面ABCD,
又,∴MNEF,
由平面ABCD,平面ABCD,从而EF平面ABCD,
又∵EG∩EF=E,平面EFGH,
∴平面EFGH平面ABCD.
44.
(1)平面,平面,则,在中,由余弦定理:,在中,由正弦定理:
,解得,又,则,于是,即,又,故平面,又平面,则平面平面.
(2)由第一问知,是平面的法向量,于是只要证明即可,即证,由向量的运算:,,两式相加得:,于是,
即,显然点平面,点平面,则直线平面,于是PQ平面.
45.
,
.
∴PQ⊥OA.
46.
以为原点,所在直线为轴,所在直线为轴,所在直线为轴,建立如图所示的空间直角坐标系,
则、、、、,所以、,
,,,,,,.
(1)因为,所以,即.
又平面,平面,所以平面;
(2)因为,所以,同理可得,
即,.
又,所以平面.
平面,所以平面平面.
47.
(1)∵面CDEF面ABCD,EDCD,面,面面,
∴ED面ABCD,面,即,
过作于,过作交于,
∵CDEF为直角梯形,AB=3EF=3,
∴,即,则,且,
∴,得,即,
∴,而,即面,又面,
∴,故.
(2)以D为原点,过点D垂直于DC的直线为x轴,DC所在直线为y轴,所在直线为z轴,建立空间直角坐标系,如下图示:
∴,若,则,
设,则,
设平面BDM的法向量为,则,取x1=2,则,
若AE∥平面BDM,则,解得,
∴线段CF上存在一点M,满足AE∥平面BDM,此时.
试卷第1页,总3页
