探索三角形全等的条件(1)[下学期]

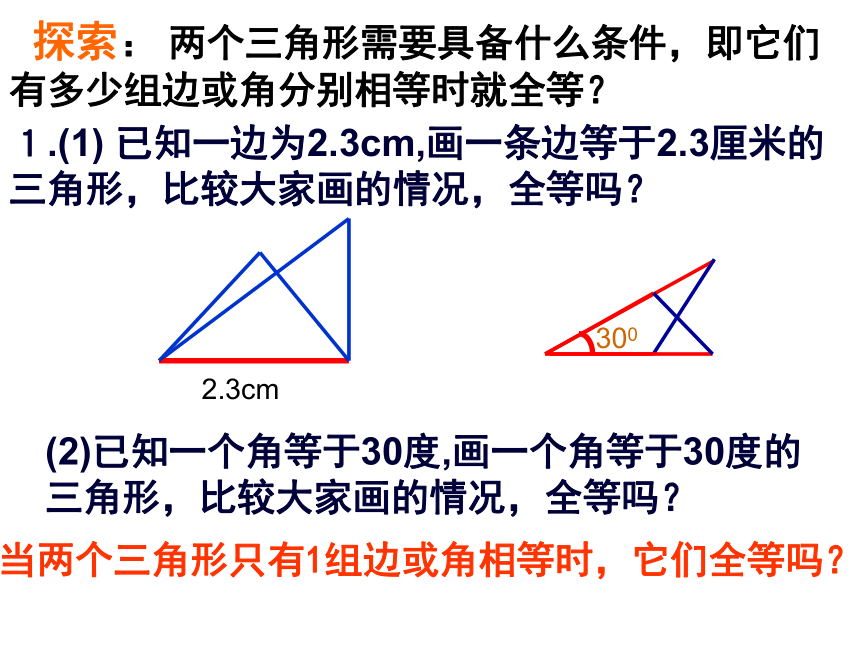
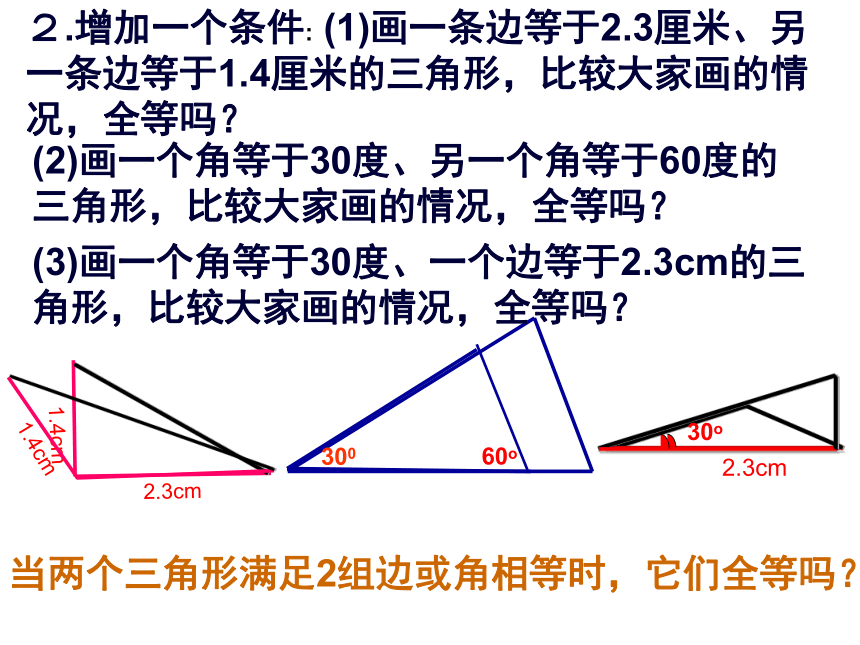
课件18张PPT。探索三角形全等的条件(1)2、如果两个三角形全等，那么它们的对应边和对应角有什么关系?一、情境导入 1、什么是全等图形、全等三角形？思考：如何判定两三角形全等１.(1) 已知一边为2.3cm,画一条边等于2.3厘米的三角形，比较大家画的情况，全等吗？(2)已知一个角等于30度,画一个角等于30度的三角形，比较大家画的情况，全等吗？当两个三角形只有1组边或角相等时，它们全等吗？2.3cm300 探索： 两个三角形需要具备什么条件，即它们有多少组边或角分别相等时就全等？２.增加一个条件: (1)画一条边等于2.3厘米、另一条边等于1.4厘米的三角形，比较大家画的情况，全等吗？(2)画一个角等于30度、另一个角等于60度的三角形，比较大家画的情况，全等吗？当两个三角形满足2组边或角相等时，它们全等吗？(3)画一个角等于30度、一个边等于2.3cm的三角形，比较大家画的情况，全等吗？３.再增加一个条件有哪几种情况？共有4种情况：
（1）两边一角；　（2）两角一边；（3）边边边；　　（4）角角角。这节课我们将研究第一种情况：两边一角｛两边和它们的夹角、两边和其中一边的对角｝ 1、用书本第111页所说的方法画三角形2、将所得的三角形剪下，并与同学进行比较， 你得出什么结论？ (1)、 画∠MAN=500；
(2)、在AM、AN上分别截取　　　 AC=1.4cm， AB=2.3cm；
(3)、连结BC。（二）按条件画三角形、比较 结论：两边和它们的夹角对应相等的两个三角形全等。简写成“边角边”或“SAS”。书第112页练一练的1。快速反应三、例题教学如图：AB=AD，∠BAC=∠DAC，⊿ABC和⊿ADC全等吗？为什么？ＡＢＣＤ变式一：(1)如果把△ABC与△ADC拉开如图形状，若要使得它们全等，还需要什么条件？(2)其他条件不变,
BC=DC吗?ABCCD变式二:如图AB=AD,AC=AF,∠BAF=∠DAC.请在图中找出全等的三角形,并说明理由.ABCFD四、拓展应用 1、书第112页练一练的2。2、如果两个三角形中有两边及其中一边的对角对应相等，这两个三角形全等吗？ABC5503.0cm2.5cmD5503.0cmEF2.5cm3、AD＝CB，AE=CF,
⊿ADF和⊿CBE全等吗？为什么？ ABCDFE∠DAF= ∠BCE,AD∥BC通过这节课的学习
你有什么
收获?本节课你学习了什么？
发现了什么？
有什么收获？
还存在什么没有解决的问题？ 1、经历了画图、剪纸、测量等方法探索三角形全等的活动过程，归纳得出了两个三角形全等的条件（—）：“SAS”，知道了有两边和其中一边的对角对应相等的两个三角形不一定全等。
２、充分利用已知条件（包括图形中隐含的公共边、公共角）；用“因为……所以……”或“因为……根据……所以……”的表达方式进行简单的说理。五、收获体会 　　生活真美，生活中有数学，我们爱生活，我们爱数学，因为它可以使我们睿智。作业教科书 第120页 习题第1、2、3祝 你 们 学 习 进 步 ！