人教版必修第一册 5.4.1 正弦函数、余弦函数的图象 课件(共27张PPT)
文档属性
| 名称 | 人教版必修第一册 5.4.1 正弦函数、余弦函数的图象 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 20:14:41 | ||
图片预览




文档简介
(共27张PPT)
正弦函数、余弦函数的图象
作业布置
1、经历绘制正弦函数图象的过程,掌握几何法,掌握绘制正弦 函数图象的“五点法”,发展学生直观想象素养。
2、经历正弦函数图象绘制余弦函数图象的过程,理解正余弦函 数之间的关系,体会图象变换的思想,发展学生逻辑推理的核心素养。
3、会用“五点法”,画出正弦函数,余弦函数的简图,通过正弦函数与余弦函数的图象的应用,提升直观想象的核心素养。
学习目标:
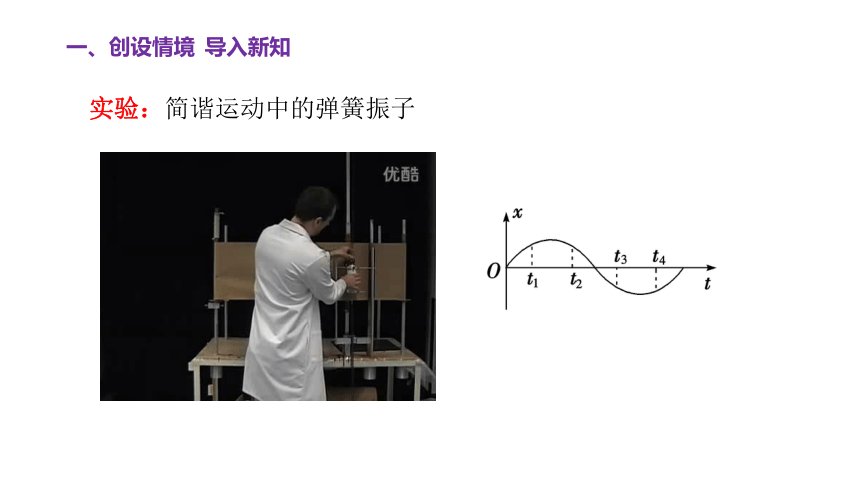
一、创设情境 导入新知
实验:简谐运动中的弹簧振子
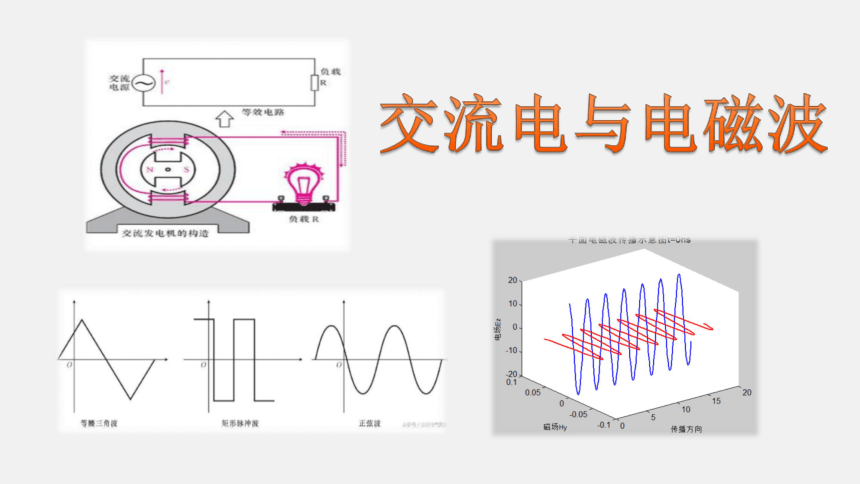
交流电与电磁波
墨尔本仿生动能雕塑
西班牙米拉之家
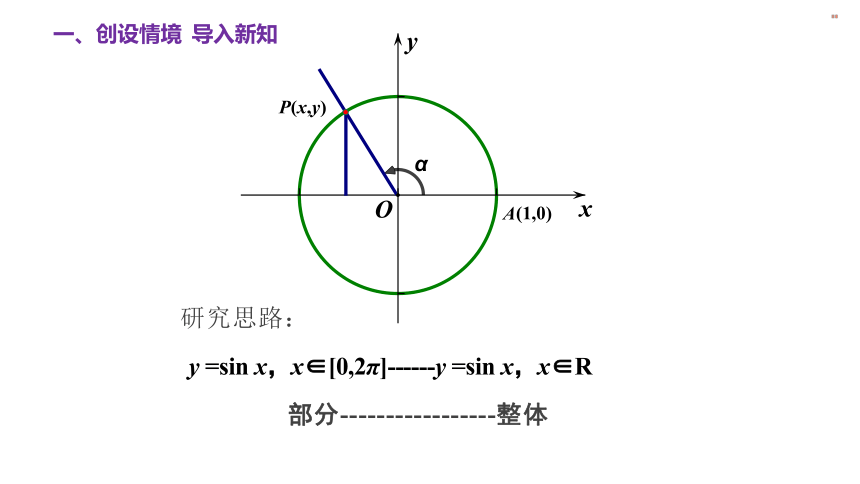
研究思路:
y =sin x,x∈[0,2π]------y =sin x,x∈R
部分-----------------整体
一、创设情境 导入新知
x
y
α
P
(
x
,
y
)
A
(1,0)
O
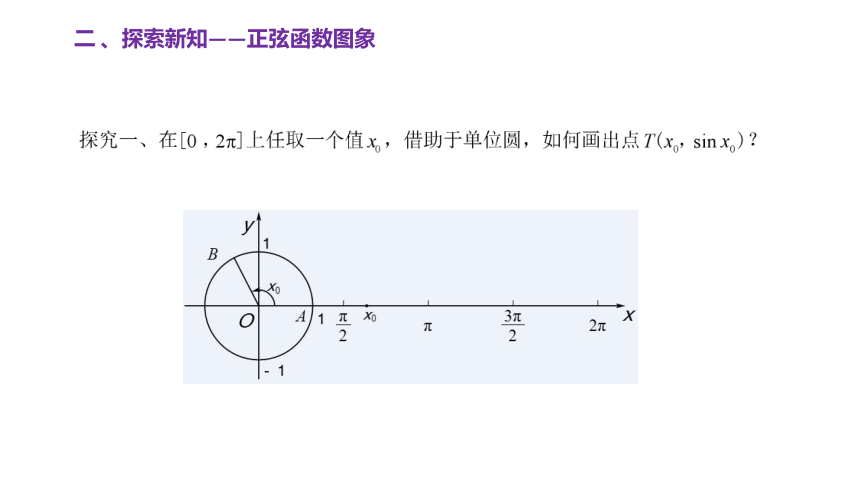
二 、探索新知——正弦函数图象
1
-1
O
y
x
●
●
●
●
●
●
●
●
●
●
●
●
●
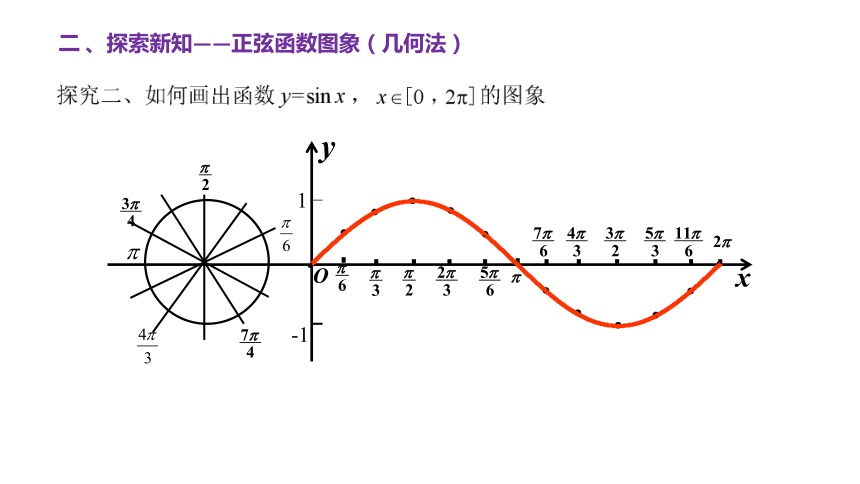
二 、探索新知——正弦函数图象(几何法)
正弦函数的图象叫做正弦曲线,“波浪起伏”的连续光滑曲线。
问题2:如何由 的图象得到 的图象
y=sinx x [0,2 ]
y=sinx x R
y
x
o
1
-1
y=sinx x [0,2 ]
y=sinx x R
观察正弦曲线,图象有什么特征?
周而复始
无限延伸
凸凹有界
对称美
问题3:对函数的研究,能够快速而又准确地做出其简图,
往往其非常重要的作用。在精确度要求不太高时,
要画出函数 的简图,应抓住哪些
关键点?
二 、探索新知——正弦函数图象
1
-1
O
y
x
●
●
●
●
●
●
●
●
●
●
●
●
●
图象与x轴的交点:
图象的最高点:
图象的最低点:
( )
( )
思考:在确定正弦函数的图象形状时,应该抓住哪些关键点?
二 、探索新知——正弦函数图象(五点法)
x
o
y
五点法作图:
1
-1
x
sinx
0
1
-1
0
0
(1) 列表
(2) 描点
(3) 连线
二 、探索新知——正弦函数图象(五点法)
列表
描点
连线
横纵坐标 列准确
坐标系中 轻描点
光滑曲线 凸凹连
“五点法”作图
二 、探索新知——正弦函数图象(五点法)
问题4:如何画出余弦函数 的图象?
方案一:几何法(余弦函数定义)
方案二:五点法
方案三:图像变化法
三 、探索新知——余弦函数图象
三 、探索新知——余弦函数图象
问题5:类比用“五点法”画正弦函数图象的方法,
如何作出余弦函数在区间 上的简图?
x
cosx
0
-1
1
0
-1
1
-1
x
y
o
三、探索新知——余弦函数图象
四、学以致用 内化素养
x
y
o
1
2
-1
上移1个单位
函数 的图象与函数 的图象有什么关系?
四、学以致用 内化素养
x
y
o
1
-1
沿 轴翻 折
函数 的图象与函数 的图象有什么关系?
四、学以致用 内化素养
性 质
应 用
画 法
几何法
作 简 图
数形结合
五 点 法
正余弦函数的图象
最高点、最低点、 与 轴的交点
图象变换
五、归纳总结 构建体系
六、课堂检测 目标达成
六、课堂检测 目标达成
生活就像正弦曲线
有时波峰有时波谷
波峰时别得意忘形
得意时不以物喜
失意时不以己悲
喜忧相伴快乐前行
立德树人 和谐发展
七、作业布置 分层训练
谢 谢
正弦函数、余弦函数的图象
作业布置
1、经历绘制正弦函数图象的过程,掌握几何法,掌握绘制正弦 函数图象的“五点法”,发展学生直观想象素养。
2、经历正弦函数图象绘制余弦函数图象的过程,理解正余弦函 数之间的关系,体会图象变换的思想,发展学生逻辑推理的核心素养。
3、会用“五点法”,画出正弦函数,余弦函数的简图,通过正弦函数与余弦函数的图象的应用,提升直观想象的核心素养。
学习目标:
一、创设情境 导入新知
实验:简谐运动中的弹簧振子
交流电与电磁波
墨尔本仿生动能雕塑
西班牙米拉之家
研究思路:
y =sin x,x∈[0,2π]------y =sin x,x∈R
部分-----------------整体
一、创设情境 导入新知
x
y
α
P
(
x
,
y
)
A
(1,0)
O
二 、探索新知——正弦函数图象
1
-1
O
y
x
●
●
●
●
●
●
●
●
●
●
●
●
●
二 、探索新知——正弦函数图象(几何法)
正弦函数的图象叫做正弦曲线,“波浪起伏”的连续光滑曲线。
问题2:如何由 的图象得到 的图象
y=sinx x [0,2 ]
y=sinx x R
y
x
o
1
-1
y=sinx x [0,2 ]
y=sinx x R
观察正弦曲线,图象有什么特征?
周而复始
无限延伸
凸凹有界
对称美
问题3:对函数的研究,能够快速而又准确地做出其简图,
往往其非常重要的作用。在精确度要求不太高时,
要画出函数 的简图,应抓住哪些
关键点?
二 、探索新知——正弦函数图象
1
-1
O
y
x
●
●
●
●
●
●
●
●
●
●
●
●
●
图象与x轴的交点:
图象的最高点:
图象的最低点:
( )
( )
思考:在确定正弦函数的图象形状时,应该抓住哪些关键点?
二 、探索新知——正弦函数图象(五点法)
x
o
y
五点法作图:
1
-1
x
sinx
0
1
-1
0
0
(1) 列表
(2) 描点
(3) 连线
二 、探索新知——正弦函数图象(五点法)
列表
描点
连线
横纵坐标 列准确
坐标系中 轻描点
光滑曲线 凸凹连
“五点法”作图
二 、探索新知——正弦函数图象(五点法)
问题4:如何画出余弦函数 的图象?
方案一:几何法(余弦函数定义)
方案二:五点法
方案三:图像变化法
三 、探索新知——余弦函数图象
三 、探索新知——余弦函数图象
问题5:类比用“五点法”画正弦函数图象的方法,
如何作出余弦函数在区间 上的简图?
x
cosx
0
-1
1
0
-1
1
-1
x
y
o
三、探索新知——余弦函数图象
四、学以致用 内化素养
x
y
o
1
2
-1
上移1个单位
函数 的图象与函数 的图象有什么关系?
四、学以致用 内化素养
x
y
o
1
-1
沿 轴翻 折
函数 的图象与函数 的图象有什么关系?
四、学以致用 内化素养
性 质
应 用
画 法
几何法
作 简 图
数形结合
五 点 法
正余弦函数的图象
最高点、最低点、 与 轴的交点
图象变换
五、归纳总结 构建体系
六、课堂检测 目标达成
六、课堂检测 目标达成
生活就像正弦曲线
有时波峰有时波谷
波峰时别得意忘形
得意时不以物喜
失意时不以己悲
喜忧相伴快乐前行
立德树人 和谐发展
七、作业布置 分层训练
谢 谢
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
