数学人教A版(2019)必修第一册4.5.2用二分法求函数近似解 课件(共30张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.5.2用二分法求函数近似解 课件(共30张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 20:15:13 | ||
图片预览









文档简介
(共30张PPT)
第四章 指数函数与对数函数
4.5.2 用二分法求函数的近似解
高中数学/人教A版/必修一
……
知识篇
素养篇
思维篇
4.5.2 用二分法求函数的近似解
1
复习回顾
零点存在定理
如果函数y=f(x)在区间[a,b]上的图象是连续不断
的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)
在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,
这个c也就是方程f(x)=0的一个根.
注意:零点存在定理只能确定零点存在,但没能准确
求出零点. (只在此山中,云深不知处!)
思考:如何求出函数f(x)=lnx+2x-6在区间(2, 3)内的
零点?
分析:一个直观的想法是,如果能将零点所在的范围
尽量缩小,那么在一定精确度的要求下,就可
以得到符合要求的零点的近似值.
为了方便,可以通过取区间中点的方法,逐步
缩小零点所在的范围.
(2,3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
(2.5,3)
f(2.5)<0,f(3)>0
2.75
f(2.75)>0
(2.5,2.75)
f(2.5)<0,f(2.75)>0
2.625
f(2.625)>0
(2.5,2.625)
f(2.5)<0,f(2.625)>0
2.562 5
f(2.562 5)>0
f(2.5)<0,f(2.562 5)>0
(2.5,2.562 5)
f(2.531 25)<0
2.531 25
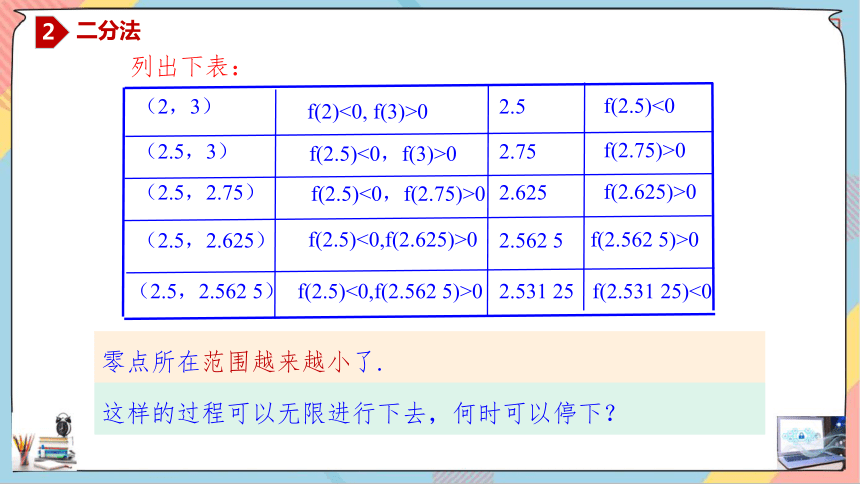
列出下表:
零点所在范围越来越小了.
这样的过程可以无限进行下去,何时可以停下?
2
二分法
2
二分法
精确度:近似值与准确值的误差限度.
问题:如果要求精确度为0.01,怎么找函数
f(x)=lnx+2x-6 在区间(2, 3)内的零点?
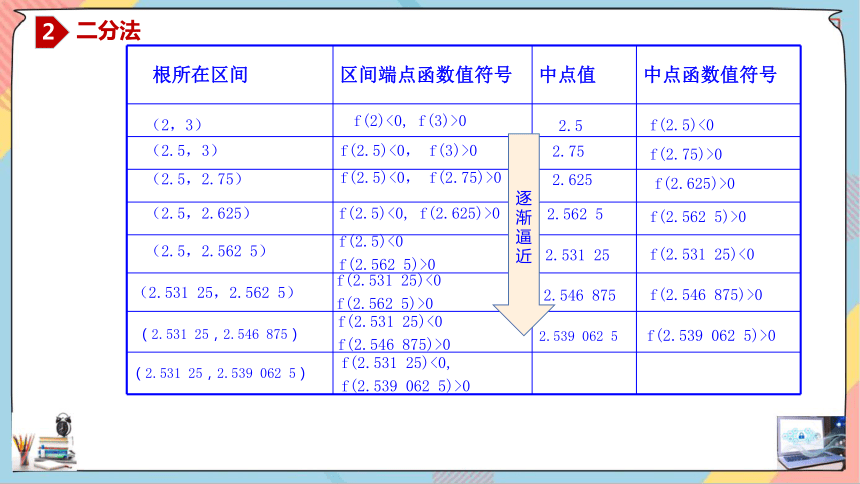
根所在区间 区间端点函数值符号 中点值 中点函数值符号
(2,3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
(2.5,3)
f(2.5)<0, f(3)>0
2.75
f(2.75)>0
(2.5,2.75)
f(2.5)<0, f(2.75)>0
2.625
f(2.625)>0
(2.5,2.625)
f(2.5)<0, f(2.625)>0
2.562 5
f(2.562 5)>0
(2.531 25,2.562 5)
f(2.5)<0
f(2.562 5)>0
(2.5,2.562 5)
f(2.531 25)<0
f(2.562 5)>0
f(2.531 25)<0
2.539 062 5
2.546 875
(2.531 25,2.546 875)
2.531 25
f(2.539 062 5)>0
f(2.531 25)<0
f(2.546 875)>0
(2.531 25,2.539 062 5)
f(2.546 875)>0
f(2.531 25)<0,
f(2.539 062 5)>0
2
二分法
逐渐逼近
由于
所以,可以将
作为函数
零点的近似值,也即方程 的近似根.
2
二分法
注意精确度
对于在区间[a,b]上_________且f(a)·f(b)<0
的函数y=f(x),通过不断地把函数f(x)的零点所在
的区间_________,使区间的两个端点逐步逼近
_____,进而得到零点近似值的方法叫做二分法.
连续不断
一分为二
零点
2
二分法
1.确定区间 ,验证 ,给定精确度ε .
2.求区间(a,b)的中点c.
3.计算
(1)若 ,则c就是函数的零点.
(2)若 ,则令b=c(此时零点x0∈(a,c)).
(3)若 ,则令a=c(此时零点x0∈(c,b)).
即若 ,则得到零点近似值a(或b);
4.判断是否达到精确度ε,
否则,重复步骤2~4.
给定精确度ε ,二分法求函数f(x)的零点近似值的步骤:
2
二分法
用二分法求方程 f(x)=0(或g(x)=h(x))近似解寻找解所在区间的方法:
(1)先画出y = f(x)的图象,观察图象与x轴的交点横坐标所处的一个区间;
(2)反复运用零点存在定理,使得零点所在区间长度越来越小,直至满足精度要求.
方法总结
2
二分法
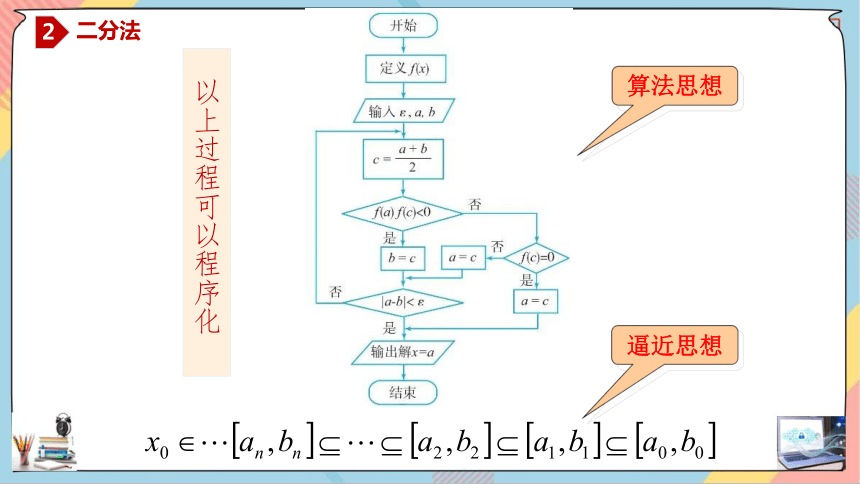
算法思想
逼近思想
以上过程可以程序化
2
二分法
练一练
用二分法求方程ln (2x+6)+2=3x的根的近似值时,令f(x)=ln(2x+6)+2-3x,并用计算器得到下表:
x 1.00 1.25 1.375 1.50
f(x) 1.0794 0.1918 -0.3604 -0.9989
则由表中的数据,可得方程ln(2x+6)+2=3x的一个近似解(精确度为0.1)为( )
A.1.125 B.1.3125 C.1.4375 D.1.46875
B
解析:原方程即2x+3x-7=0,令f(x)=2x+3x-7,用计算器或计算机作出函数 f(x)=2x+3x-7的对应值表:
273
142
75
40
21
10
3
-2
-6
f(x)
8
7
6
5
4
3
2
1
0
x
例1.借助计算器或计算机用二分法求方程2x+3x=7的
近似解(精确度0.1).
接着作出函数图象如下:
3
典型例题
因为f(1)·f(2)<0,
所以 f(x)=2x+3x-7在区间(1,2)
内有零点x0;
取区间(1,2)的中点x1=1.5,f(1.5)≈ 0.33,
因为f(1)·f(1.5)<0,
所以x0 ∈(1,1.5)
3
典型例题
取区间(1,1.5)的中点x2=1.25 ,
f(1.25)≈-0.87,
因为f(1.25)·f(1.5)<0,
所以x0∈(1.25,1.5);
同理可得,x0∈(1.375,1.5),
x0∈(1.375,1.437 5),
由于|1.375-1.437 5|=0.062 5<0.1
所以,原方程的近似解可取为1.437 5.
3
典型例题
B
练一练
1.用二分法求函数f(x)在(a,b)内的唯一零点时,精确度
为0.001,则结束计算的条件是( )
A.|a-b|<0.1 B.|a-b|<0.001
C.|a-b|>0.001 D.|a-b|=0.001
答案: B
练一练
2.用二分法求方程x3-2x-5=0在区间(2,4)上的实数根时,取中点x1=3,则下一个含有根的区间是________.
答案: (2,3)
B
练一练
答案: B
3.函数f(x)=ln(x+1)-的零点所在的大致区间是( )
A.(0,1) B.(1,2)
C.(2,e) D.(3,4)
4.利用计算器,求方程lgx=3-x的近似解.(精确度0.1)
解:画出y=lgx及y=3-x的图象,观察图象得,方程lgx=3-x
有唯一解,记为x1,且这个解在区间(2,3)内.
设 f(x)=lgx+x-3
y
1
3
3
x
o
练一练
因为|2.625-2.562 5|=0.062 5<0.1,所以可以将x=2.625作为原方程的一个近似解.
根所在区间 区间端点函数值 符号 中点值 中点函数值符号
(2,3)
f(2)<0,f(3)>0
2.5
f(2.5)<0
(2.5,3)
f(2.5)<0,f(3)>0
2.75
f(2.75)>0
(2.5,2.75)
f(2.5)<0,f(2.75)>0
2.625
f(2.625)>0
(2.5,2.625)
f(2.5)<0,f(2.625)>0
2.562 5
f(2.562 5)<0
(2.562 5,2.625)
f(2.562 5)<0,
f(2.625)>0
列出下表:
n分法的比较
用二分法寻找函数零点的过程,就是一个“精益求精”的收敛的过程.
问题1:为什么用二分法,而不用三分法、四分法…?
4
理论拓展
逐一法
二分法
7次
3次
三分法
4次
四分法
4次
按“最不利原则”
在“最不利原则”下,每试验一次 二分法 三分法 四分法 逐一法
排查范围缩小为原来的
最优策略(效率最高)
收敛速度
4
理论拓展
“二分法”因其简单高效,在生产生活中的应用非常广泛,比如检修线路故障、血液检测标本、查找次品、猜数问题等。
4
理论拓展
问题2:用二分法时只能取中点吗?与其它的取点方法之
间有没有优劣之分?
4
理论拓展
(课后思考,查找相关资料)
课堂小结
一、本节课学习的新知识
二分法的概念
二分法的操作程序
函数零点个数的确定
二、本节课提升的核心素养
数据分析
课堂小结
数学建模
数学运算
三、本节课训练的数学思想方法
转化与化归
课堂小结
函数与方程思想
数形结合
01
基础作业: .
02
能力作业: .
03
拓展延伸:(选做)
作业
第四章 指数函数与对数函数
4.5.2 用二分法求函数的近似解
高中数学/人教A版/必修一
……
知识篇
素养篇
思维篇
4.5.2 用二分法求函数的近似解
1
复习回顾
零点存在定理
如果函数y=f(x)在区间[a,b]上的图象是连续不断
的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)
在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,
这个c也就是方程f(x)=0的一个根.
注意:零点存在定理只能确定零点存在,但没能准确
求出零点. (只在此山中,云深不知处!)
思考:如何求出函数f(x)=lnx+2x-6在区间(2, 3)内的
零点?
分析:一个直观的想法是,如果能将零点所在的范围
尽量缩小,那么在一定精确度的要求下,就可
以得到符合要求的零点的近似值.
为了方便,可以通过取区间中点的方法,逐步
缩小零点所在的范围.
(2,3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
(2.5,3)
f(2.5)<0,f(3)>0
2.75
f(2.75)>0
(2.5,2.75)
f(2.5)<0,f(2.75)>0
2.625
f(2.625)>0
(2.5,2.625)
f(2.5)<0,f(2.625)>0
2.562 5
f(2.562 5)>0
f(2.5)<0,f(2.562 5)>0
(2.5,2.562 5)
f(2.531 25)<0
2.531 25
列出下表:
零点所在范围越来越小了.
这样的过程可以无限进行下去,何时可以停下?
2
二分法
2
二分法
精确度:近似值与准确值的误差限度.
问题:如果要求精确度为0.01,怎么找函数
f(x)=lnx+2x-6 在区间(2, 3)内的零点?
根所在区间 区间端点函数值符号 中点值 中点函数值符号
(2,3)
f(2)<0, f(3)>0
2.5
f(2.5)<0
(2.5,3)
f(2.5)<0, f(3)>0
2.75
f(2.75)>0
(2.5,2.75)
f(2.5)<0, f(2.75)>0
2.625
f(2.625)>0
(2.5,2.625)
f(2.5)<0, f(2.625)>0
2.562 5
f(2.562 5)>0
(2.531 25,2.562 5)
f(2.5)<0
f(2.562 5)>0
(2.5,2.562 5)
f(2.531 25)<0
f(2.562 5)>0
f(2.531 25)<0
2.539 062 5
2.546 875
(2.531 25,2.546 875)
2.531 25
f(2.539 062 5)>0
f(2.531 25)<0
f(2.546 875)>0
(2.531 25,2.539 062 5)
f(2.546 875)>0
f(2.531 25)<0,
f(2.539 062 5)>0
2
二分法
逐渐逼近
由于
所以,可以将
作为函数
零点的近似值,也即方程 的近似根.
2
二分法
注意精确度
对于在区间[a,b]上_________且f(a)·f(b)<0
的函数y=f(x),通过不断地把函数f(x)的零点所在
的区间_________,使区间的两个端点逐步逼近
_____,进而得到零点近似值的方法叫做二分法.
连续不断
一分为二
零点
2
二分法
1.确定区间 ,验证 ,给定精确度ε .
2.求区间(a,b)的中点c.
3.计算
(1)若 ,则c就是函数的零点.
(2)若 ,则令b=c(此时零点x0∈(a,c)).
(3)若 ,则令a=c(此时零点x0∈(c,b)).
即若 ,则得到零点近似值a(或b);
4.判断是否达到精确度ε,
否则,重复步骤2~4.
给定精确度ε ,二分法求函数f(x)的零点近似值的步骤:
2
二分法
用二分法求方程 f(x)=0(或g(x)=h(x))近似解寻找解所在区间的方法:
(1)先画出y = f(x)的图象,观察图象与x轴的交点横坐标所处的一个区间;
(2)反复运用零点存在定理,使得零点所在区间长度越来越小,直至满足精度要求.
方法总结
2
二分法
算法思想
逼近思想
以上过程可以程序化
2
二分法
练一练
用二分法求方程ln (2x+6)+2=3x的根的近似值时,令f(x)=ln(2x+6)+2-3x,并用计算器得到下表:
x 1.00 1.25 1.375 1.50
f(x) 1.0794 0.1918 -0.3604 -0.9989
则由表中的数据,可得方程ln(2x+6)+2=3x的一个近似解(精确度为0.1)为( )
A.1.125 B.1.3125 C.1.4375 D.1.46875
B
解析:原方程即2x+3x-7=0,令f(x)=2x+3x-7,用计算器或计算机作出函数 f(x)=2x+3x-7的对应值表:
273
142
75
40
21
10
3
-2
-6
f(x)
8
7
6
5
4
3
2
1
0
x
例1.借助计算器或计算机用二分法求方程2x+3x=7的
近似解(精确度0.1).
接着作出函数图象如下:
3
典型例题
因为f(1)·f(2)<0,
所以 f(x)=2x+3x-7在区间(1,2)
内有零点x0;
取区间(1,2)的中点x1=1.5,f(1.5)≈ 0.33,
因为f(1)·f(1.5)<0,
所以x0 ∈(1,1.5)
3
典型例题
取区间(1,1.5)的中点x2=1.25 ,
f(1.25)≈-0.87,
因为f(1.25)·f(1.5)<0,
所以x0∈(1.25,1.5);
同理可得,x0∈(1.375,1.5),
x0∈(1.375,1.437 5),
由于|1.375-1.437 5|=0.062 5<0.1
所以,原方程的近似解可取为1.437 5.
3
典型例题
B
练一练
1.用二分法求函数f(x)在(a,b)内的唯一零点时,精确度
为0.001,则结束计算的条件是( )
A.|a-b|<0.1 B.|a-b|<0.001
C.|a-b|>0.001 D.|a-b|=0.001
答案: B
练一练
2.用二分法求方程x3-2x-5=0在区间(2,4)上的实数根时,取中点x1=3,则下一个含有根的区间是________.
答案: (2,3)
B
练一练
答案: B
3.函数f(x)=ln(x+1)-的零点所在的大致区间是( )
A.(0,1) B.(1,2)
C.(2,e) D.(3,4)
4.利用计算器,求方程lgx=3-x的近似解.(精确度0.1)
解:画出y=lgx及y=3-x的图象,观察图象得,方程lgx=3-x
有唯一解,记为x1,且这个解在区间(2,3)内.
设 f(x)=lgx+x-3
y
1
3
3
x
o
练一练
因为|2.625-2.562 5|=0.062 5<0.1,所以可以将x=2.625作为原方程的一个近似解.
根所在区间 区间端点函数值 符号 中点值 中点函数值符号
(2,3)
f(2)<0,f(3)>0
2.5
f(2.5)<0
(2.5,3)
f(2.5)<0,f(3)>0
2.75
f(2.75)>0
(2.5,2.75)
f(2.5)<0,f(2.75)>0
2.625
f(2.625)>0
(2.5,2.625)
f(2.5)<0,f(2.625)>0
2.562 5
f(2.562 5)<0
(2.562 5,2.625)
f(2.562 5)<0,
f(2.625)>0
列出下表:
n分法的比较
用二分法寻找函数零点的过程,就是一个“精益求精”的收敛的过程.
问题1:为什么用二分法,而不用三分法、四分法…?
4
理论拓展
逐一法
二分法
7次
3次
三分法
4次
四分法
4次
按“最不利原则”
在“最不利原则”下,每试验一次 二分法 三分法 四分法 逐一法
排查范围缩小为原来的
最优策略(效率最高)
收敛速度
4
理论拓展
“二分法”因其简单高效,在生产生活中的应用非常广泛,比如检修线路故障、血液检测标本、查找次品、猜数问题等。
4
理论拓展
问题2:用二分法时只能取中点吗?与其它的取点方法之
间有没有优劣之分?
4
理论拓展
(课后思考,查找相关资料)
课堂小结
一、本节课学习的新知识
二分法的概念
二分法的操作程序
函数零点个数的确定
二、本节课提升的核心素养
数据分析
课堂小结
数学建模
数学运算
三、本节课训练的数学思想方法
转化与化归
课堂小结
函数与方程思想
数形结合
01
基础作业: .
02
能力作业: .
03
拓展延伸:(选做)
作业
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
