人教版数学必修第一册 3.2.2 奇偶性 课件(共25张PPT)
文档属性
| 名称 | 人教版数学必修第一册 3.2.2 奇偶性 课件(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 21.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 21:01:53 | ||
图片预览







文档简介
(共25张PPT)
3.2
函数的基本性质
3.2.2
奇偶性(第1课时)
莱州市第六中学
张力萍
温故知新
前面我们用符号语言精确地描述了函数图象在定义域的某个区间上”上
升”(”下降”)的性质。还记得咱们的研究思路吗?
具体函数一图象特征→数量刻画一符号语言一→抽象定义
数形结合
由特殊到一
抽象概括
生活中的“对称美
”
y
入
WHEN
优通酷
WHEN
A MATHEMATICIAN
A MATHEMATICIAN
DANCES
DANCES
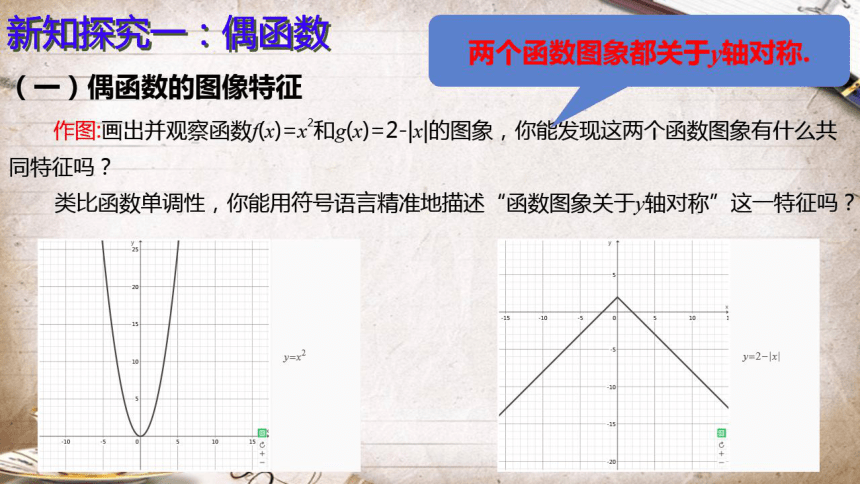
新知探究一:偶函数
两个函数图象都关于y对称
(一)偶函数的图像特征
作图:画出并观察函数x)=x和g(x)=2-x的图象,你能发现这两个函数图象有什么共
同特征吗?
类比函数单调性,你能用符号语言精准地描述“函数图象关于轴对称”这一特征吗?
y=2-x
国
回
15
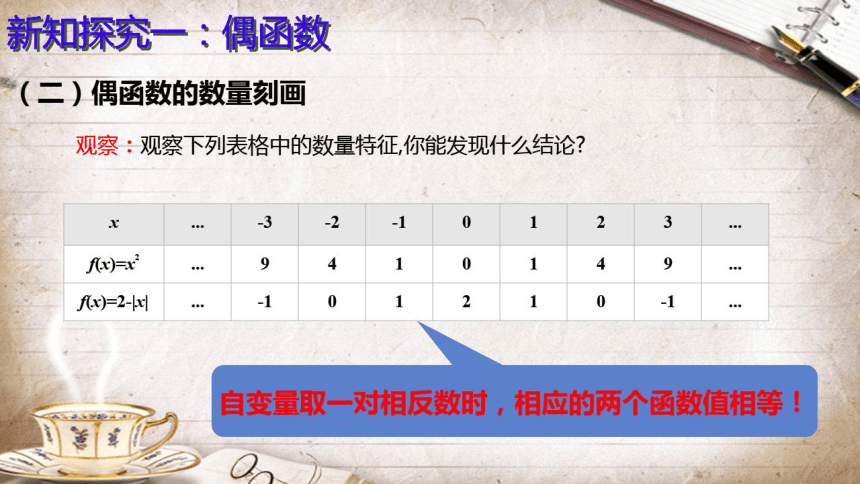
新知探究一:偶函数
(二)偶函数的数量刻画
观察:观察下列表格中的数量特征,你能发现什么结论?
x
-3
-2
-1
0
1
2
3
Ax)=x
9
4
1
0
1
4
9
fx)-2-kxl
-1
0
1
2
1
0
-1
白变量取一对相反数时,相应的两个函数值相等
新知探究一:偶函数
x
-3
-2
Ax)=x
9
(三)偶函数的符号语言
fx)=2-
-1
小组合作:1.如何用数学语言描述该结论?
2.该结论是否具有一般性?
自变量取一对相反数时
3如何说明该结论具有一般性?
相应的两个函数值相等
例如:对于x)=x
术-3)=9=3)
VxER,f(-x)=(-x)2=x2=f(x),
-2)=4=2)
这时称f(x)为偶函数、
-1)=1=1)
X)
新知探究一:偶函数
定义域关于原点对称!
(四)偶函数的定义
般地,设函数fx)的定义域为,如果Vx∈,都有-x∈I,
且-x)=x),那么函数f(x)叫做偶函数.
辨析
1对于函数fx)=x2,当定义域如下时,是否为偶函数?
A.fx)的定义域为(-1,1]
B.f八x)的定义域为(-o,0)U(0,+oo)
C.f(x)的定义域为(-oo,1)U(1,+o)
2fx)的定义域为(-3,3)
新知探究一:偶函数
定义域关于原点对称!
(四)偶函数的定义
般地,设函数f(x)的定义域为I,如果Vx∈I,都有-x∈I,
且f-x)=(x),那么函数f代x)叫做偶函数.
任意性
辨析2.己知x)的定义域为R,下列说法是否正确?
A.若f代-2)=f(2),则函数f(x)是偶函数。
B.若f代-2)≠f(2),则函数f(x)不是偶函数。
3.2
函数的基本性质
3.2.2
奇偶性(第1课时)
莱州市第六中学
张力萍
温故知新
前面我们用符号语言精确地描述了函数图象在定义域的某个区间上”上
升”(”下降”)的性质。还记得咱们的研究思路吗?
具体函数一图象特征→数量刻画一符号语言一→抽象定义
数形结合
由特殊到一
抽象概括
生活中的“对称美
”
y
入
WHEN
优通酷
WHEN
A MATHEMATICIAN
A MATHEMATICIAN
DANCES
DANCES
新知探究一:偶函数
两个函数图象都关于y对称
(一)偶函数的图像特征
作图:画出并观察函数x)=x和g(x)=2-x的图象,你能发现这两个函数图象有什么共
同特征吗?
类比函数单调性,你能用符号语言精准地描述“函数图象关于轴对称”这一特征吗?
y=2-x
国
回
15
新知探究一:偶函数
(二)偶函数的数量刻画
观察:观察下列表格中的数量特征,你能发现什么结论?
x
-3
-2
-1
0
1
2
3
Ax)=x
9
4
1
0
1
4
9
fx)-2-kxl
-1
0
1
2
1
0
-1
白变量取一对相反数时,相应的两个函数值相等
新知探究一:偶函数
x
-3
-2
Ax)=x
9
(三)偶函数的符号语言
fx)=2-
-1
小组合作:1.如何用数学语言描述该结论?
2.该结论是否具有一般性?
自变量取一对相反数时
3如何说明该结论具有一般性?
相应的两个函数值相等
例如:对于x)=x
术-3)=9=3)
VxER,f(-x)=(-x)2=x2=f(x),
-2)=4=2)
这时称f(x)为偶函数、
-1)=1=1)
X)
新知探究一:偶函数
定义域关于原点对称!
(四)偶函数的定义
般地,设函数fx)的定义域为,如果Vx∈,都有-x∈I,
且-x)=x),那么函数f(x)叫做偶函数.
辨析
1对于函数fx)=x2,当定义域如下时,是否为偶函数?
A.fx)的定义域为(-1,1]
B.f八x)的定义域为(-o,0)U(0,+oo)
C.f(x)的定义域为(-oo,1)U(1,+o)
2fx)的定义域为(-3,3)
新知探究一:偶函数
定义域关于原点对称!
(四)偶函数的定义
般地,设函数f(x)的定义域为I,如果Vx∈I,都有-x∈I,
且f-x)=(x),那么函数f代x)叫做偶函数.
任意性
辨析2.己知x)的定义域为R,下列说法是否正确?
A.若f代-2)=f(2),则函数f(x)是偶函数。
B.若f代-2)≠f(2),则函数f(x)不是偶函数。
同课章节目录
