苏教版选择性必修第一册3.3.1抛物线的标准方程 同步教学课件(共51张PPT)
文档属性
| 名称 | 苏教版选择性必修第一册3.3.1抛物线的标准方程 同步教学课件(共51张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-21 21:14:05 | ||
图片预览









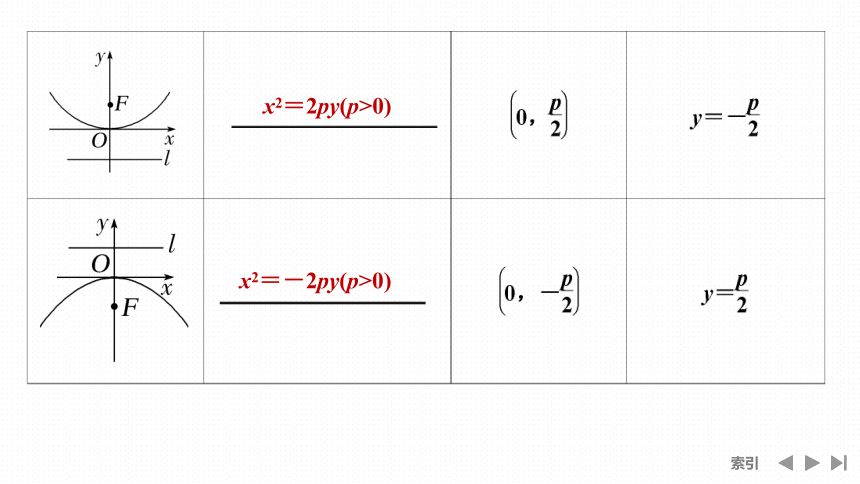


文档简介
(共51张PPT)
第3章 圆锥曲线与方程
3.3 抛物线
3.3.1 抛物线的标准方程
课标要求
1.掌握抛物线的标准方程,能根据已知条件求抛物线的标准方程.
2.能根据抛物线的标准方程求焦点坐标和准线方程.3.能利用抛物线的定义和标准方程求最值.
素养要求
1.借助抛物线标准方程的推导,提升数学运算素养.2.借助最值问题,提升直观想象与逻辑推理素养.
问题导学预习教材
必备知识探究
内容
索引
互动合作研析题型
关键能力提升
拓展延伸分层精练
核心素养达成
WEN TI DAO XUE YU XI JIAO CAI BI BEI ZHI SHI TAN JIU
问题导学预习教材 必备知识探究
1
一、抛物线的定义
1.思考 抛物线可以看成双曲线的一支对吗?
提示 双曲线与抛物线上的点的性质存在着差异,虽然抛物线的形状与双曲线的形状看起来有点“像”,但绝不能把抛物线看成是双曲线的一支.
2.填空 平面内到一个定点F和一条定直线l(F不在l上)的__________的点的轨迹叫作________.定点F叫作抛物线的______,定直线l叫作抛物线的______.
温馨提醒 (1)定义的实质可归结为“一动三定”:一个动点,设为M;一个定点F叫作抛物线的焦点;一条定直线l叫作抛物线的准线;一个定值,即点M与点F的距离和它到直线l的距离之比等于1.
(2)注意定点F不在定直线l上,否则动点M的轨迹不是抛物线,而是过点F垂直于直线l的一条直线.
例如,到点F(0,1)与到直线l:x+y-1=0的距离相等的点的轨迹方程为x-y+1=0,轨迹是一条直线.
距离相等
抛物线
焦点
准线
BC
3.做一做 (多选)下列命题是假命题的是( )
A.到定点F(-1,0)和定直线x=1的距离相等的动点P的轨迹为抛物线
B.到定点F(2,1)和定直线3x-2y-4=0的距离相等的动点P的轨迹为抛物线
C.抛物线的焦点一定在y轴上
D.抛物线的标准方程中,p表示焦点到准线的距离,p的值永远大于0
解析 由抛物线定义易得A是真命题;B是假命题,因为定点F(2,1)在定直线3x-2y-4=0上,所以动点P的轨迹为直线;C是假命题,抛物线的焦点的位置可以随抛物线方程的不同而不同,比如y2=2x的焦点在x轴上.D明显正确.
二、抛物线的标准方程
1.思考 比较椭圆、双曲线标准方程的建立过程,你认为如何建立坐标系,可能使所求抛物线的方程形式简单?
2.填空
y2=2px(p>0)
y2=-2px(p>0)
x2=2py(p>0)
x2=-2py(p>0)
温馨提醒 (1)p的几何意义是焦点到准线的距离.
(2)标准方程的结构特征:顶点在坐标原点、焦点在坐标轴上.
(3)抛物线的开口方向:抛物线的开口方向取决于一次项变量(x或y)的取值范围.
C
HU DONG HE ZUO YAN XI TI XING GUAN JIAN MENG LI TI SHENG
互动合作研析题型 关键能力提升
2
例1 分别求满足下列条件的抛物线的标准方程.
(1)焦点为(-2,0);
(2)准线为y=-1;
题型一 求抛物线的标准方程
∴p=4,∴抛物线的标准方程为y2=-8x.
求抛物线的标准方程主要利用待定系数法,其步骤为
(1)依据条件设出抛物线的标准方程的类型.
(2)求参数p的值.
(3)确定抛物线的标准方程.1
思维升华
特别提醒 当焦点位置不确定时,应分类讨论,也可以设y2=ax或x2=ay(a≠0)的形式,以简化讨论过程.
训练1 分别求满足下列条件的抛物线的标准方程:
(1)过点(3,-4);
解 法一 ∵点(3,-4)在第四象限,
∴设抛物线的标准方程为y2=2px (p>0)或x2=-2p1y (p1>0).
把点(3,-4)的坐标分别代入y2=2px和x2=-2p1y,
得(-4)2=2p·3,32=-2p1·(-4),
法二 抛物线的方程可设为y2=ax (a≠0)或x2=by (b≠0).
(2)焦点在直线x+3y+15=0上.
解 令x=0得y=-5;令y=0得x=-15.
∴抛物线的焦点为(0,-5)或(-15,0).
∴所求抛物线的标准方程为x2=-20y或y2=-60x.
A
题型二 抛物线定义的应用
(2)已知点P是抛物线y2=2x上的一个动点,求点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值.
解 由抛物线的定义可知,抛物线上的点到准线的距离等于它到焦点的距离.
迁移1 若将本例(2)中的点(0,2)改为点A(3,2),求PA+PF的最小值.
解 将x=3代入y2=2x,
抛物线定义在求最值中的应用
(1)解此类最值问题时,首先要注意抛物线定义的转化应用,其次是注意平面几何知识的应用,例如两点之间线段最短,三角形中三边间的不等关系,点与直线上点的连线垂线段最短等.
(2)数形结合是求解几何最值的常用方法之一.
思维升华
训练2 已知定长为3的线段AB的端点A,B在抛物线y2=x上移动,求AB的中点M到y轴距离的最小值.
解 如图,设点F是抛物线y2=x的焦点,过A,B两点分别作其准线的垂线AC,BD,过AB的中点M作准线的垂线MN,C,D,N为垂足,
题型三 抛物线的实际应用问题
例3 河上有一抛物线形拱桥,当水面距拱桥顶5 m时,水面宽为8 m,一小船宽4 m,高2 m,载货后船露出水面上的部分高0.75 m,问:水面上涨到与抛物线拱桥拱顶相距多少米时,小船开始不能通航?
(1)解决本题的关键是把实际问题转化为数学问题,利用数学模型,通过数学语言(文字、符号、图形、字母等)表达、分析、解决问题.
(2)以抛物线为数学模型的实例很多,如拱桥、隧道、喷泉等,应用抛物线解决问题主要体现在:①建立适当的平面直角坐标系,求抛物线的标准方程;②利用已求方程求点的坐标.
(3)求解抛物线实际应用题的步骤:
思维升华
训练3 探照灯反光镜的纵断面是抛物线的一部分,光源在抛物线的焦点处,已知灯口直径是60 cm,灯深40 cm,则光源到反光镜顶点的距离是( )
A.11.25 cm B.5.625 cm
C.20 cm D.10 cm
B
解析 如图,
建立平面直角坐标系,设抛物线方程是y2=2px(p>0).
∵A(40,30)在抛物线上,
课堂小结
1.牢记2个知识点
(1)抛物线的定义.
(2)抛物线的标准方程.
2.掌握2种解决问题的方法
(1)求标准方程的方法.
(2)运用定义解决有关距离的最值问题的方法.
3.注意1个易错点
忽视抛物线的开口方向而致误.
TUO ZHAN YAN SHEN FEN CENG JING LIAN HE XING SU YANG DA CHENG
拓展延伸分层精练 核心素养达成
3
1.抛物线y2=-8x的焦点坐标是( )
A.(2,0) B.(-2,0)
C.(4,0) D.(-4,0)
B
解析 ∵y2=-8x,∴p=4,
∴焦点坐标为(-2,0).
2.若动点P与定点F(1,1)和直线l:3x+y-4=0的距离相等,则动点P的轨迹是( )
A.椭圆 B.双曲线
C.抛物线 D.直线
D
整理,得x2+9y2+4x-12y-6xy+4=0,
即(x-3y+2)2=0,∴x-3y+2=0.所以动点P的轨迹为直线.
法二 显然定点F(1,1)在直线l:3x+y-4=0上,则与定点F和直线l距离相等的动点P的轨迹是过F点且与直线l垂直的一条直线.
3.顶点在原点,对称轴是y轴,并且顶点与焦点的距离等于3的抛物线的标准方程是( )
A.x2=±3y B.y2=±6x
C.x2=±12y D.x2=±6y
C
4.(多选)对标准形式的抛物线,给出下列条件:
①焦点在y轴上;②焦点在x轴上;③抛物线上横坐标为1的点到焦点的距离等于6;④由原点向过焦点的某直线作垂线,垂足坐标为(2,1).
其中满足抛物线方程为y2=10x的是( )
A.① B.② C.③ D.④
BD
5.(多选)经过点P(4,-2)的抛物线的标准方程可以为( )
A.y2=x B.x2=8y
C.x2=-8y D.y2=-8x
AC
解析 当抛物线的焦点在x轴上时,
设抛物线的方程为y2=2px(p>0),
又因为抛物线经过点P(4,-2),
所以抛物线的方程为y2=x.
当抛物线的焦点在y轴上时,
设抛物线的方程为x2=-2py(p>0),
又因为抛物线经过点P(4,-2),
所以42=-2p×(-2),解得p=4,
所以抛物线的方程为x2=-8y.
综上,抛物线的方程为y2=x或x2=-8y.
6.若抛物线方程为7x+4y2=0,则焦点坐标为______________.
8.如图所示,设P是曲线y2=4x上的一个动点,则点P到点B(-1,1)的距离与点P到直线x=-1的距离之和的最小值为________.
10.如图所示,一隧道内设双行线公路,其截面由长方形的三条边和抛物线的一段构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米.
(1)以隧道的顶点为原点O,其对称轴所在的直线为y轴,建立平面直角坐标系(如图),求该抛物线的方程;
解 依题意,
所以该抛物线的方程为x2=-5y.
(2)若行车道总宽度AB为7米,请计算通过隧道的车辆限制高度为多少米(精确到0.1米).
解 设车辆高h米,则DB=h+0.5,
故D(3.5,h-6.5),
代入方程x2=-5y,解得h=4.05,
所以车辆通过隧道的限制高度为4.0米.
A
11.顶点在原点,对称轴为坐标轴,焦点为直线3x-4y-12=0与坐标轴的交点的抛物线的标准方程为( )
A.x2=-12y或y2=16x B.x2=12y或y2=-16x
C.x2=9y或y2=12x D.x2=-9y或y2=-12x
解析 对于直线方程3x-4y-12=0,
令x=0,得y=-3;令y=0,得x=4,
所以抛物线的焦点为(0,-3)或(4,0).
当焦点为(0,-3)时,设抛物线方程为x2=-2py(p>0),
ABC
又AF=4,故MF=2,
设准线与x轴的交点为N.
∵p=2,∴NF=FM=2,故△AMF≌△DNF,
∴F为AD的中点,故B正确;
D
本课结束
第3章 圆锥曲线与方程
3.3 抛物线
3.3.1 抛物线的标准方程
课标要求
1.掌握抛物线的标准方程,能根据已知条件求抛物线的标准方程.
2.能根据抛物线的标准方程求焦点坐标和准线方程.3.能利用抛物线的定义和标准方程求最值.
素养要求
1.借助抛物线标准方程的推导,提升数学运算素养.2.借助最值问题,提升直观想象与逻辑推理素养.
问题导学预习教材
必备知识探究
内容
索引
互动合作研析题型
关键能力提升
拓展延伸分层精练
核心素养达成
WEN TI DAO XUE YU XI JIAO CAI BI BEI ZHI SHI TAN JIU
问题导学预习教材 必备知识探究
1
一、抛物线的定义
1.思考 抛物线可以看成双曲线的一支对吗?
提示 双曲线与抛物线上的点的性质存在着差异,虽然抛物线的形状与双曲线的形状看起来有点“像”,但绝不能把抛物线看成是双曲线的一支.
2.填空 平面内到一个定点F和一条定直线l(F不在l上)的__________的点的轨迹叫作________.定点F叫作抛物线的______,定直线l叫作抛物线的______.
温馨提醒 (1)定义的实质可归结为“一动三定”:一个动点,设为M;一个定点F叫作抛物线的焦点;一条定直线l叫作抛物线的准线;一个定值,即点M与点F的距离和它到直线l的距离之比等于1.
(2)注意定点F不在定直线l上,否则动点M的轨迹不是抛物线,而是过点F垂直于直线l的一条直线.
例如,到点F(0,1)与到直线l:x+y-1=0的距离相等的点的轨迹方程为x-y+1=0,轨迹是一条直线.
距离相等
抛物线
焦点
准线
BC
3.做一做 (多选)下列命题是假命题的是( )
A.到定点F(-1,0)和定直线x=1的距离相等的动点P的轨迹为抛物线
B.到定点F(2,1)和定直线3x-2y-4=0的距离相等的动点P的轨迹为抛物线
C.抛物线的焦点一定在y轴上
D.抛物线的标准方程中,p表示焦点到准线的距离,p的值永远大于0
解析 由抛物线定义易得A是真命题;B是假命题,因为定点F(2,1)在定直线3x-2y-4=0上,所以动点P的轨迹为直线;C是假命题,抛物线的焦点的位置可以随抛物线方程的不同而不同,比如y2=2x的焦点在x轴上.D明显正确.
二、抛物线的标准方程
1.思考 比较椭圆、双曲线标准方程的建立过程,你认为如何建立坐标系,可能使所求抛物线的方程形式简单?
2.填空
y2=2px(p>0)
y2=-2px(p>0)
x2=2py(p>0)
x2=-2py(p>0)
温馨提醒 (1)p的几何意义是焦点到准线的距离.
(2)标准方程的结构特征:顶点在坐标原点、焦点在坐标轴上.
(3)抛物线的开口方向:抛物线的开口方向取决于一次项变量(x或y)的取值范围.
C
HU DONG HE ZUO YAN XI TI XING GUAN JIAN MENG LI TI SHENG
互动合作研析题型 关键能力提升
2
例1 分别求满足下列条件的抛物线的标准方程.
(1)焦点为(-2,0);
(2)准线为y=-1;
题型一 求抛物线的标准方程
∴p=4,∴抛物线的标准方程为y2=-8x.
求抛物线的标准方程主要利用待定系数法,其步骤为
(1)依据条件设出抛物线的标准方程的类型.
(2)求参数p的值.
(3)确定抛物线的标准方程.1
思维升华
特别提醒 当焦点位置不确定时,应分类讨论,也可以设y2=ax或x2=ay(a≠0)的形式,以简化讨论过程.
训练1 分别求满足下列条件的抛物线的标准方程:
(1)过点(3,-4);
解 法一 ∵点(3,-4)在第四象限,
∴设抛物线的标准方程为y2=2px (p>0)或x2=-2p1y (p1>0).
把点(3,-4)的坐标分别代入y2=2px和x2=-2p1y,
得(-4)2=2p·3,32=-2p1·(-4),
法二 抛物线的方程可设为y2=ax (a≠0)或x2=by (b≠0).
(2)焦点在直线x+3y+15=0上.
解 令x=0得y=-5;令y=0得x=-15.
∴抛物线的焦点为(0,-5)或(-15,0).
∴所求抛物线的标准方程为x2=-20y或y2=-60x.
A
题型二 抛物线定义的应用
(2)已知点P是抛物线y2=2x上的一个动点,求点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值.
解 由抛物线的定义可知,抛物线上的点到准线的距离等于它到焦点的距离.
迁移1 若将本例(2)中的点(0,2)改为点A(3,2),求PA+PF的最小值.
解 将x=3代入y2=2x,
抛物线定义在求最值中的应用
(1)解此类最值问题时,首先要注意抛物线定义的转化应用,其次是注意平面几何知识的应用,例如两点之间线段最短,三角形中三边间的不等关系,点与直线上点的连线垂线段最短等.
(2)数形结合是求解几何最值的常用方法之一.
思维升华
训练2 已知定长为3的线段AB的端点A,B在抛物线y2=x上移动,求AB的中点M到y轴距离的最小值.
解 如图,设点F是抛物线y2=x的焦点,过A,B两点分别作其准线的垂线AC,BD,过AB的中点M作准线的垂线MN,C,D,N为垂足,
题型三 抛物线的实际应用问题
例3 河上有一抛物线形拱桥,当水面距拱桥顶5 m时,水面宽为8 m,一小船宽4 m,高2 m,载货后船露出水面上的部分高0.75 m,问:水面上涨到与抛物线拱桥拱顶相距多少米时,小船开始不能通航?
(1)解决本题的关键是把实际问题转化为数学问题,利用数学模型,通过数学语言(文字、符号、图形、字母等)表达、分析、解决问题.
(2)以抛物线为数学模型的实例很多,如拱桥、隧道、喷泉等,应用抛物线解决问题主要体现在:①建立适当的平面直角坐标系,求抛物线的标准方程;②利用已求方程求点的坐标.
(3)求解抛物线实际应用题的步骤:
思维升华
训练3 探照灯反光镜的纵断面是抛物线的一部分,光源在抛物线的焦点处,已知灯口直径是60 cm,灯深40 cm,则光源到反光镜顶点的距离是( )
A.11.25 cm B.5.625 cm
C.20 cm D.10 cm
B
解析 如图,
建立平面直角坐标系,设抛物线方程是y2=2px(p>0).
∵A(40,30)在抛物线上,
课堂小结
1.牢记2个知识点
(1)抛物线的定义.
(2)抛物线的标准方程.
2.掌握2种解决问题的方法
(1)求标准方程的方法.
(2)运用定义解决有关距离的最值问题的方法.
3.注意1个易错点
忽视抛物线的开口方向而致误.
TUO ZHAN YAN SHEN FEN CENG JING LIAN HE XING SU YANG DA CHENG
拓展延伸分层精练 核心素养达成
3
1.抛物线y2=-8x的焦点坐标是( )
A.(2,0) B.(-2,0)
C.(4,0) D.(-4,0)
B
解析 ∵y2=-8x,∴p=4,
∴焦点坐标为(-2,0).
2.若动点P与定点F(1,1)和直线l:3x+y-4=0的距离相等,则动点P的轨迹是( )
A.椭圆 B.双曲线
C.抛物线 D.直线
D
整理,得x2+9y2+4x-12y-6xy+4=0,
即(x-3y+2)2=0,∴x-3y+2=0.所以动点P的轨迹为直线.
法二 显然定点F(1,1)在直线l:3x+y-4=0上,则与定点F和直线l距离相等的动点P的轨迹是过F点且与直线l垂直的一条直线.
3.顶点在原点,对称轴是y轴,并且顶点与焦点的距离等于3的抛物线的标准方程是( )
A.x2=±3y B.y2=±6x
C.x2=±12y D.x2=±6y
C
4.(多选)对标准形式的抛物线,给出下列条件:
①焦点在y轴上;②焦点在x轴上;③抛物线上横坐标为1的点到焦点的距离等于6;④由原点向过焦点的某直线作垂线,垂足坐标为(2,1).
其中满足抛物线方程为y2=10x的是( )
A.① B.② C.③ D.④
BD
5.(多选)经过点P(4,-2)的抛物线的标准方程可以为( )
A.y2=x B.x2=8y
C.x2=-8y D.y2=-8x
AC
解析 当抛物线的焦点在x轴上时,
设抛物线的方程为y2=2px(p>0),
又因为抛物线经过点P(4,-2),
所以抛物线的方程为y2=x.
当抛物线的焦点在y轴上时,
设抛物线的方程为x2=-2py(p>0),
又因为抛物线经过点P(4,-2),
所以42=-2p×(-2),解得p=4,
所以抛物线的方程为x2=-8y.
综上,抛物线的方程为y2=x或x2=-8y.
6.若抛物线方程为7x+4y2=0,则焦点坐标为______________.
8.如图所示,设P是曲线y2=4x上的一个动点,则点P到点B(-1,1)的距离与点P到直线x=-1的距离之和的最小值为________.
10.如图所示,一隧道内设双行线公路,其截面由长方形的三条边和抛物线的一段构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米.
(1)以隧道的顶点为原点O,其对称轴所在的直线为y轴,建立平面直角坐标系(如图),求该抛物线的方程;
解 依题意,
所以该抛物线的方程为x2=-5y.
(2)若行车道总宽度AB为7米,请计算通过隧道的车辆限制高度为多少米(精确到0.1米).
解 设车辆高h米,则DB=h+0.5,
故D(3.5,h-6.5),
代入方程x2=-5y,解得h=4.05,
所以车辆通过隧道的限制高度为4.0米.
A
11.顶点在原点,对称轴为坐标轴,焦点为直线3x-4y-12=0与坐标轴的交点的抛物线的标准方程为( )
A.x2=-12y或y2=16x B.x2=12y或y2=-16x
C.x2=9y或y2=12x D.x2=-9y或y2=-12x
解析 对于直线方程3x-4y-12=0,
令x=0,得y=-3;令y=0,得x=4,
所以抛物线的焦点为(0,-3)或(4,0).
当焦点为(0,-3)时,设抛物线方程为x2=-2py(p>0),
ABC
又AF=4,故MF=2,
设准线与x轴的交点为N.
∵p=2,∴NF=FM=2,故△AMF≌△DNF,
∴F为AD的中点,故B正确;
D
本课结束
