图形的旋转 周练(湖北省黄冈市英山县)
文档属性
| 名称 | 图形的旋转 周练(湖北省黄冈市英山县) | 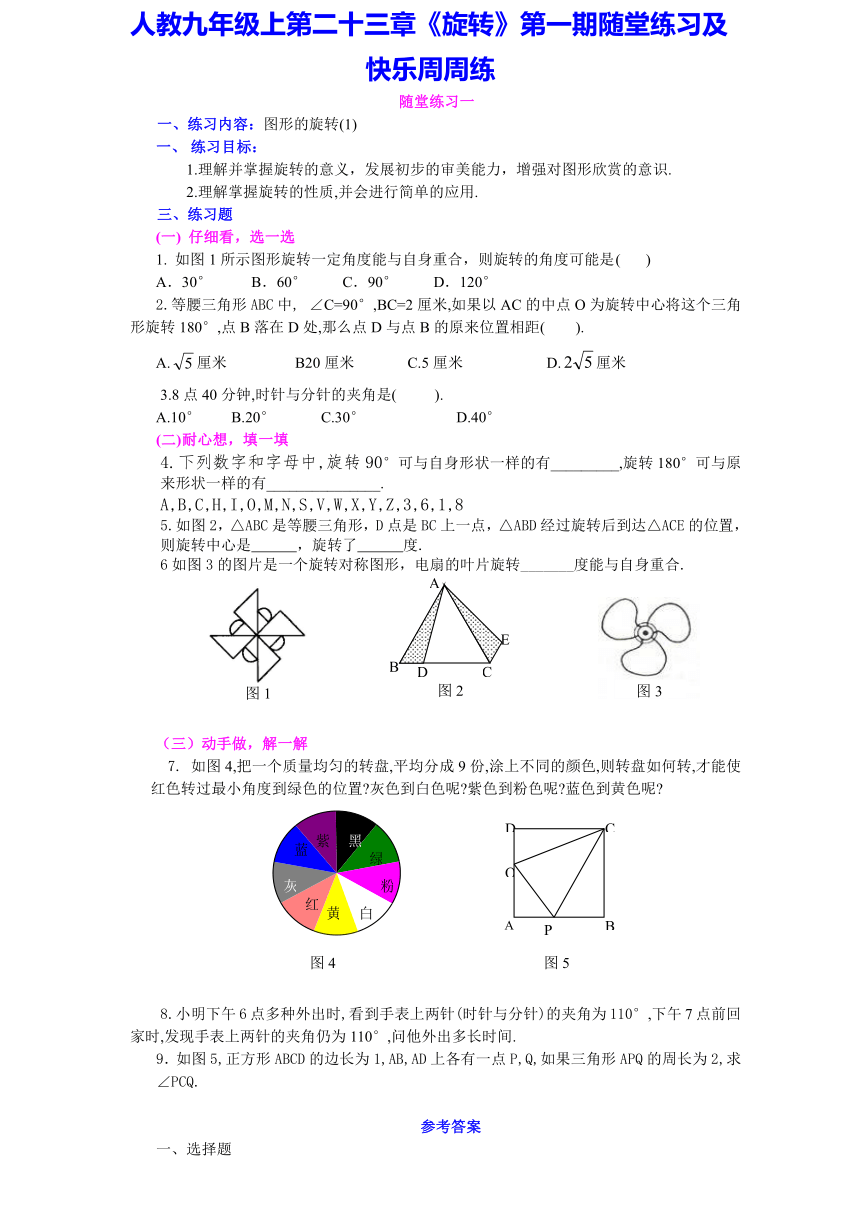 | |
| 格式 | rar | ||
| 文件大小 | 90.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-09-29 21:28:00 | ||
图片预览



文档简介
人教九年级上第二十三章《旋转》第一期随堂练习及
快乐周周练
随堂练习一
一、练习内容:图形的旋转(1)
1、 练习目标:
1.理解并掌握旋转的意义,发展初步的审美能力,增强对图形欣赏的意识.
2.理解掌握旋转的性质,并会进行简单的应用.
三、练习题
(一) 仔细看,选一选
1. 如图1所示图形旋转一定角度能与自身重合,则旋转的角度可能是 ( )
A.30° B.60° C.90° D.120°
2.等腰三角形ABC中, ∠C=90°,BC=2厘米,如果以AC的中点O为旋转中心将这个三角形旋转180°,点B落在D处,那么点D与点B的原来位置相距( ).
A.厘米 B20厘米 C.5厘米 D.厘米
3.8点40分钟,时针与分针的夹角是( ).
A.10° B.20° C.30° D.40°
(2) 耐心想,填一填
4.下列数字和字母中,旋转90°可与自身形状一样的有_________,旋转180°可与原来形状一样的有_______________.
A,B,C,H,I,O,M,N,S,V,W,X,Y,Z,3,6,1,8
5.如图2,△ABC是等腰三角形,D点是BC上一点,△ABD经过旋转后到达△ACE的位置,则旋转中心是 ,旋转了 度.
6如图3的图片是一个旋转对称图形,电扇的叶片旋转_______度能与自身重合.
(三)动手做,解一解
7. 如图4,把一个质量均匀的转盘,平均分成9份,涂上不同的颜色,则转盘如何转,才能使红色转过最小角度到绿色的位置 灰色到白色呢 紫色到粉色呢 蓝色到黄色呢
8.小明下午6点多种外出时,看到手表上两针(时针与分针)的夹角为110°,下午7点前回家时,发现手表上两针的夹角仍为110°,问他外出多长时间.
9.如图5,正方形ABCD的边长为1,AB,AD上各有一点P,Q,如果三角形APQ的周长为2,求∠PCQ.
参考答案
一、选择题
1.C 2.C 3.B
二、填空题
4.O和X;H,I,O,X,S,N,Z,8,1 5.点A;60° 6.120°
三、解答题
7.红色→绿色:顺时针,160°;灰色→白色:顺时针,120°;紫色→粉色:逆时针,
120°;蓝色→黄色:顺时针,120°.
8.40分钟 提示:设小明外出x分钟,依题意,有6x-0.5x=2×110,解锝x=40(分钟).
9.将△DCQ绕点C逆时针旋转90°到△BCE处,设AP=X,AQ=Y,则PB=1-X,QD=1-Y=BE,
PE=PB+BE=2-(X+Y)=2-(AP+AQ)=PQ,于是△PCQ≌△PCE(SSS),从而∠PCQ=∠PCE=45°.
随堂练习二
一、练习内容:图形的旋转(2)
练习目标:
1.能够按要求作出简单平面图形旋转后的图形.
2.要注意用尺规准确地画旋转图形.
三、练习题
(一) 仔细看,选一选
1.将三角形绕直线l旋转一周,可以得到下图所示的立体图形的是( ).
2.如图所示的图形沿旋转中心旋转多少度后能与自身重合( ).
A.120° ,180° , ()° B.180°,120°, 60°
C. 120°,60°,180° D.120°,180°,60°
3.如图,Rt△ABC的边BC绕点C旋转到CE的位置,则下列说法中正确的是( )
A.点B与点D为对应点,且∠ACD=∠BCE B.∠ACB=∠BCE
C.线段AB与线段CE是对应线段 D.AB=DE
(二)耐心想,填一填
4.观察下面的图案,它可以看作是由 经过 得到的.( )
A.图形的三分之一,平移 B.图形的四分之一,平移
C.图形的三分之一,旋转 D.图形的四分之一,旋转
5.钟表的分针旋转120度所需时间为 分;时针转3小时,旋转了 度.
6.图形是等腰直角三角形,若将它绕其直角顶点连续三次旋转90度,分别得到图形、、,则由、、、组合而成的图形为________.
7.已知长方形ABCD,绕点A将它顺时针连续旋转3次,请画出得到的图形。
8. 如图,P是正方形ABCD内一点,将△ABP绕点B顺时针
方向旋转与△CBP′重合,若PB=3,求PP′的长.
参考答案
一、选择题
1.B 2.A 3.D
二、填空题
4.图形的四分之一,旋转; 5.20;90; 6.正方形
2、 解答题
3、 7.如图所示
8. ∵ PB=3,又∵ △BP′C是由△ABP绕B点顺时针旋转产生,知∠ABP=∠P′BC,BP=BP′
∴ ∠PBP′=90°,即△PBP′是等腰直角三角形.
∴ .
快乐周周练一
[每周必读]
本周主要学习了图形旋转的有关概念及其性质,重点是通过具体实例认识旋转,理解旋转前后两个图形对应点到旋转中心距离相等,对应点与旋转中心的连线所成的角彼此相等的性质。并会利用这些性质解决问题。同时还要掌握简单平面图形旋转后图形的作法。
(一)仔细看,选一选(每小题4分,共28分)
1.下列运动是属于旋转的是( ).
A.动过程中的篮球的滚动 B.表的钟摆的摆动
C.球升空的运动 D.个图形沿某直线对折过程
2.经过旋转,下列说法中错误的是( ).
(A)图形上的每一点到旋转中心的距离相等
(B)图形上每一点转动的角度都相等
(C)图形上可能存在不动点
(D)图形上任意两点的连线与其对应两点的连线相等
3.如图1,ΔABC和ΔADE都是等腰直角三角形,∠C和∠ADE都是直角,点C在AE上,ΔABC绕着A点经过逆时针旋转后能够与ΔADE重合得到图1,再将图1作为“基本图形”绕着A点经过逆时针连续旋转得到图2.两次旋转的角度分别为( ).
图1 图2
(A)45°,90°;(B)90°,45°;(C)60°,30°;(D)30°,60°
4.如图所示图形旋转一定角度能与自身重合,则旋转的角度可能是( ).
A.30° B.60° C.90° D.120°
5.下列图形中,绕某个点旋转能与自身重合的有( )
①正方形 ②长方形 ③等边三角形 ④线段 ⑤角 ⑥平行四边形
A. 5个 B.2个 C.3个 D.4个
6.将图形按顺时针方向旋转900后的图形是( ).
A B C D
7.下列基本图形中,经过平移、旋转或轴对称变换后,不能得到右图的是( ).
A. B.
C. D.
(二)耐心想,填一填(每小题4分,共28分)
8.如图(1),以左边图案的中心为旋转中心,将
图案按 方向旋转 即可得到左边图案。
9.图(2)绕着中心最小旋转 能与自身重合。
10.如图,当半径为30cm的转动轮转过120角时,传送带上的物体A平移的距离为 cm。
11.如图,从甲到乙的变换关系分别为:①:_______ ②:_______③:________
12.一个等腰三角形经过5次旋转得到的五角星,其旋转角度是__________.
13.从8:55到9:15,钟表的分针转动的角度是 ,时针转动的角度是 .
14.如果一个长方形ABCD的长为10厘米,宽为6厘米,现将它绕它的对称中
心旋转90度后达到四边形AˊBˊCˊDˊ的位置,那么长方形ABCD与四边形
AˊBˊCˊDˊ重合部分的面积为__________.
(三)动手做,解一解(15。16每题7分,17题10分,共24分)
15.如图是日本“三菱”汽车的标志,它可以看作是由什么“基本图案”通过怎样旋转得到的?每次旋转了多少度?
16.如图,把绕B点逆时针方向旋转30 后,画出旋转后的三角形。
17..如图,四边形ABCD的∠BAD=∠C=90 ,AB=AD,AE⊥BC于E,旋转后能与重合。
(1) 旋转中心是哪一点
(2) 旋转了多少度
(3) 若AE=5㎝,求四边形AECF的面积。
四、创新应用(每题10分,共20分)
18.如图,在10×5的正方形网格中,每个小正方形的边长均为单位1,将△ABC向右平移4个单位,得到△A′B′C′,再把△A′B′C′绕点A′逆时针旋转90°,得到△A″B″C″.请你画出△A′B′C′和△A″B″C″(不要求写画法)
例2.现有如图所示的六种瓷砖,请用其中的4块或6块瓷砖(准许使用相同的),设计出美丽的图案.
例如:
19.阅读下面材料:
如图(1),把△ABC沿直线BC平行移动线段BC的长度,可以变到△DEC的位置;
如图(2),以BC为轴,把△ABC翻折180 ,可以变到△DBC的位置;
如图(3),以点A为中心,把△ABC旋转180 ,可以变到△AED的位置.
像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的.这种只改变位置,不改变形状大小的图形变换,叫做三角形的全等变换.
回答下列问题:
①在下图中,可以通过平行移动、翻折、旋转中的哪一种方法怎样变化,使△ABE变到△ADF的位置;
②指图中线段BE与DF之间的关系,为什么?
五、探索拓展(每小问10分,共20分)
20.已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
(1) 如图1, 连结DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请说明理由,若不正确请举反例说明;
(2) 若将正方形AEFG绕点A按顺时针方向旋转, 连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.
参考答案
一、选择题
1.B 2.A 3.A 4.C 5.D 6.D 7.C
二、填空题
8.顺时针,80° 9.90° 10.20 11.①翻转②旋转③平移 12.72° 13.120°,10° 14.36㎝2
三、解答题
15.◇,顺时针旋转120° 16.
17. ①旋转中心是点A ②逆时针旋转90°
③∵△ABE≌△ADF ∴∠F=∠AEB=90°AE=AF ∠FAD=∠BAE
∴∠FAE=∠BAD=90° ∵∠AEC=90°∠C =90° ∴四边形AECF是矩形
∵AE=AF ∴四边形AECF是正方形 ∴正方形AECF的面积是s=AE2=25CM2
四、创新应用
18.略 19.① △ABE逆时针旋转90°到△ADF 的位置. ②BE=DF.
4、 探索拓展
20.①在旋转的过程中线段DF与BF的长始终相等.”是错误的如图2 ②BE=DG, 连接BE ,
∵AG=AE ∠DAG=∠BAE AD=AB ∴△ADG≌△ABE ∴DG=BE
D
A
B
C
E
图3
图1
图2
P
Q
C
B
D
A
红
黄
白
粉
绿
黑
紫
蓝
灰
图5
图4
(2)
(1)
甲
乙
甲
乙
乙
甲
( ① )
( ③ )
( ② )
第3题图
第4题图
第8题图
第1题图
D
C
B
A
第7题图
第7题图
第4题图
第12题图
快乐周周练
随堂练习一
一、练习内容:图形的旋转(1)
1、 练习目标:
1.理解并掌握旋转的意义,发展初步的审美能力,增强对图形欣赏的意识.
2.理解掌握旋转的性质,并会进行简单的应用.
三、练习题
(一) 仔细看,选一选
1. 如图1所示图形旋转一定角度能与自身重合,则旋转的角度可能是 ( )
A.30° B.60° C.90° D.120°
2.等腰三角形ABC中, ∠C=90°,BC=2厘米,如果以AC的中点O为旋转中心将这个三角形旋转180°,点B落在D处,那么点D与点B的原来位置相距( ).
A.厘米 B20厘米 C.5厘米 D.厘米
3.8点40分钟,时针与分针的夹角是( ).
A.10° B.20° C.30° D.40°
(2) 耐心想,填一填
4.下列数字和字母中,旋转90°可与自身形状一样的有_________,旋转180°可与原来形状一样的有_______________.
A,B,C,H,I,O,M,N,S,V,W,X,Y,Z,3,6,1,8
5.如图2,△ABC是等腰三角形,D点是BC上一点,△ABD经过旋转后到达△ACE的位置,则旋转中心是 ,旋转了 度.
6如图3的图片是一个旋转对称图形,电扇的叶片旋转_______度能与自身重合.
(三)动手做,解一解
7. 如图4,把一个质量均匀的转盘,平均分成9份,涂上不同的颜色,则转盘如何转,才能使红色转过最小角度到绿色的位置 灰色到白色呢 紫色到粉色呢 蓝色到黄色呢
8.小明下午6点多种外出时,看到手表上两针(时针与分针)的夹角为110°,下午7点前回家时,发现手表上两针的夹角仍为110°,问他外出多长时间.
9.如图5,正方形ABCD的边长为1,AB,AD上各有一点P,Q,如果三角形APQ的周长为2,求∠PCQ.
参考答案
一、选择题
1.C 2.C 3.B
二、填空题
4.O和X;H,I,O,X,S,N,Z,8,1 5.点A;60° 6.120°
三、解答题
7.红色→绿色:顺时针,160°;灰色→白色:顺时针,120°;紫色→粉色:逆时针,
120°;蓝色→黄色:顺时针,120°.
8.40分钟 提示:设小明外出x分钟,依题意,有6x-0.5x=2×110,解锝x=40(分钟).
9.将△DCQ绕点C逆时针旋转90°到△BCE处,设AP=X,AQ=Y,则PB=1-X,QD=1-Y=BE,
PE=PB+BE=2-(X+Y)=2-(AP+AQ)=PQ,于是△PCQ≌△PCE(SSS),从而∠PCQ=∠PCE=45°.
随堂练习二
一、练习内容:图形的旋转(2)
练习目标:
1.能够按要求作出简单平面图形旋转后的图形.
2.要注意用尺规准确地画旋转图形.
三、练习题
(一) 仔细看,选一选
1.将三角形绕直线l旋转一周,可以得到下图所示的立体图形的是( ).
2.如图所示的图形沿旋转中心旋转多少度后能与自身重合( ).
A.120° ,180° , ()° B.180°,120°, 60°
C. 120°,60°,180° D.120°,180°,60°
3.如图,Rt△ABC的边BC绕点C旋转到CE的位置,则下列说法中正确的是( )
A.点B与点D为对应点,且∠ACD=∠BCE B.∠ACB=∠BCE
C.线段AB与线段CE是对应线段 D.AB=DE
(二)耐心想,填一填
4.观察下面的图案,它可以看作是由 经过 得到的.( )
A.图形的三分之一,平移 B.图形的四分之一,平移
C.图形的三分之一,旋转 D.图形的四分之一,旋转
5.钟表的分针旋转120度所需时间为 分;时针转3小时,旋转了 度.
6.图形是等腰直角三角形,若将它绕其直角顶点连续三次旋转90度,分别得到图形、、,则由、、、组合而成的图形为________.
7.已知长方形ABCD,绕点A将它顺时针连续旋转3次,请画出得到的图形。
8. 如图,P是正方形ABCD内一点,将△ABP绕点B顺时针
方向旋转与△CBP′重合,若PB=3,求PP′的长.
参考答案
一、选择题
1.B 2.A 3.D
二、填空题
4.图形的四分之一,旋转; 5.20;90; 6.正方形
2、 解答题
3、 7.如图所示
8. ∵ PB=3,又∵ △BP′C是由△ABP绕B点顺时针旋转产生,知∠ABP=∠P′BC,BP=BP′
∴ ∠PBP′=90°,即△PBP′是等腰直角三角形.
∴ .
快乐周周练一
[每周必读]
本周主要学习了图形旋转的有关概念及其性质,重点是通过具体实例认识旋转,理解旋转前后两个图形对应点到旋转中心距离相等,对应点与旋转中心的连线所成的角彼此相等的性质。并会利用这些性质解决问题。同时还要掌握简单平面图形旋转后图形的作法。
(一)仔细看,选一选(每小题4分,共28分)
1.下列运动是属于旋转的是( ).
A.动过程中的篮球的滚动 B.表的钟摆的摆动
C.球升空的运动 D.个图形沿某直线对折过程
2.经过旋转,下列说法中错误的是( ).
(A)图形上的每一点到旋转中心的距离相等
(B)图形上每一点转动的角度都相等
(C)图形上可能存在不动点
(D)图形上任意两点的连线与其对应两点的连线相等
3.如图1,ΔABC和ΔADE都是等腰直角三角形,∠C和∠ADE都是直角,点C在AE上,ΔABC绕着A点经过逆时针旋转后能够与ΔADE重合得到图1,再将图1作为“基本图形”绕着A点经过逆时针连续旋转得到图2.两次旋转的角度分别为( ).
图1 图2
(A)45°,90°;(B)90°,45°;(C)60°,30°;(D)30°,60°
4.如图所示图形旋转一定角度能与自身重合,则旋转的角度可能是( ).
A.30° B.60° C.90° D.120°
5.下列图形中,绕某个点旋转能与自身重合的有( )
①正方形 ②长方形 ③等边三角形 ④线段 ⑤角 ⑥平行四边形
A. 5个 B.2个 C.3个 D.4个
6.将图形按顺时针方向旋转900后的图形是( ).
A B C D
7.下列基本图形中,经过平移、旋转或轴对称变换后,不能得到右图的是( ).
A. B.
C. D.
(二)耐心想,填一填(每小题4分,共28分)
8.如图(1),以左边图案的中心为旋转中心,将
图案按 方向旋转 即可得到左边图案。
9.图(2)绕着中心最小旋转 能与自身重合。
10.如图,当半径为30cm的转动轮转过120角时,传送带上的物体A平移的距离为 cm。
11.如图,从甲到乙的变换关系分别为:①:_______ ②:_______③:________
12.一个等腰三角形经过5次旋转得到的五角星,其旋转角度是__________.
13.从8:55到9:15,钟表的分针转动的角度是 ,时针转动的角度是 .
14.如果一个长方形ABCD的长为10厘米,宽为6厘米,现将它绕它的对称中
心旋转90度后达到四边形AˊBˊCˊDˊ的位置,那么长方形ABCD与四边形
AˊBˊCˊDˊ重合部分的面积为__________.
(三)动手做,解一解(15。16每题7分,17题10分,共24分)
15.如图是日本“三菱”汽车的标志,它可以看作是由什么“基本图案”通过怎样旋转得到的?每次旋转了多少度?
16.如图,把绕B点逆时针方向旋转30 后,画出旋转后的三角形。
17..如图,四边形ABCD的∠BAD=∠C=90 ,AB=AD,AE⊥BC于E,旋转后能与重合。
(1) 旋转中心是哪一点
(2) 旋转了多少度
(3) 若AE=5㎝,求四边形AECF的面积。
四、创新应用(每题10分,共20分)
18.如图,在10×5的正方形网格中,每个小正方形的边长均为单位1,将△ABC向右平移4个单位,得到△A′B′C′,再把△A′B′C′绕点A′逆时针旋转90°,得到△A″B″C″.请你画出△A′B′C′和△A″B″C″(不要求写画法)
例2.现有如图所示的六种瓷砖,请用其中的4块或6块瓷砖(准许使用相同的),设计出美丽的图案.
例如:
19.阅读下面材料:
如图(1),把△ABC沿直线BC平行移动线段BC的长度,可以变到△DEC的位置;
如图(2),以BC为轴,把△ABC翻折180 ,可以变到△DBC的位置;
如图(3),以点A为中心,把△ABC旋转180 ,可以变到△AED的位置.
像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的.这种只改变位置,不改变形状大小的图形变换,叫做三角形的全等变换.
回答下列问题:
①在下图中,可以通过平行移动、翻折、旋转中的哪一种方法怎样变化,使△ABE变到△ADF的位置;
②指图中线段BE与DF之间的关系,为什么?
五、探索拓展(每小问10分,共20分)
20.已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
(1) 如图1, 连结DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请说明理由,若不正确请举反例说明;
(2) 若将正方形AEFG绕点A按顺时针方向旋转, 连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.
参考答案
一、选择题
1.B 2.A 3.A 4.C 5.D 6.D 7.C
二、填空题
8.顺时针,80° 9.90° 10.20 11.①翻转②旋转③平移 12.72° 13.120°,10° 14.36㎝2
三、解答题
15.◇,顺时针旋转120° 16.
17. ①旋转中心是点A ②逆时针旋转90°
③∵△ABE≌△ADF ∴∠F=∠AEB=90°AE=AF ∠FAD=∠BAE
∴∠FAE=∠BAD=90° ∵∠AEC=90°∠C =90° ∴四边形AECF是矩形
∵AE=AF ∴四边形AECF是正方形 ∴正方形AECF的面积是s=AE2=25CM2
四、创新应用
18.略 19.① △ABE逆时针旋转90°到△ADF 的位置. ②BE=DF.
4、 探索拓展
20.①在旋转的过程中线段DF与BF的长始终相等.”是错误的如图2 ②BE=DG, 连接BE ,
∵AG=AE ∠DAG=∠BAE AD=AB ∴△ADG≌△ABE ∴DG=BE
D
A
B
C
E
图3
图1
图2
P
Q
C
B
D
A
红
黄
白
粉
绿
黑
紫
蓝
灰
图5
图4
(2)
(1)
甲
乙
甲
乙
乙
甲
( ① )
( ③ )
( ② )
第3题图
第4题图
第8题图
第1题图
D
C
B
A
第7题图
第7题图
第4题图
第12题图
同课章节目录
