漳州 正弦定理、余弦定理的应用[上学期]
文档属性
| 名称 | 漳州 正弦定理、余弦定理的应用[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 38.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-07-21 09:30:00 | ||
图片预览



文档简介
课件9张PPT。1.2.1 应用举例
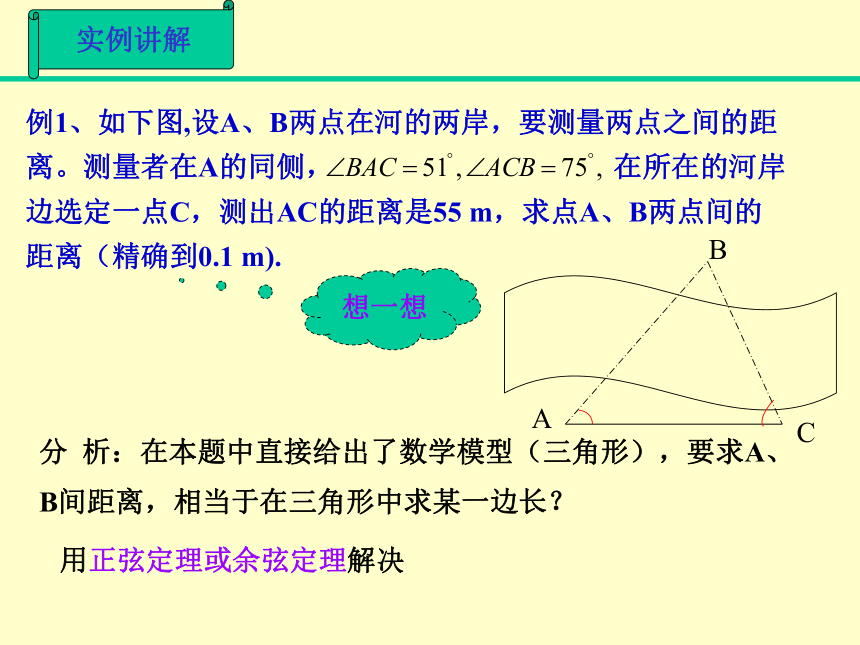
解决有关测量距离的问题知识回顾1、正弦定理:2、余弦定理:二、应 用:一、定理内容:求三角形中的某些元素实例讲解分 析:在本题中直接给出了数学模型(三角形),要求A、B间距离,相当于在三角形中求某一边长?想一想例1、如下图,设A、B两点在河的两岸,要测量两点之间的距 离。测量者在A的同侧, 在所在的河岸边选定一点C,测出AC的距离是55 m,求点A、B两点间的距离(精确到0.1 m).用正弦定理或余弦定理解决实例讲解答:A、B两点的距离为65.7米.解:分析:用正弦定理解决,只须求出 进而求出边AB的长。如果对例1的题目进行修改:点A、B都在河的对岸
且不可到达,那又如何求A、B两点间的距离?请同
学们设计一种方法求A、B两点间的距离。(如图)实例讲解想一想ACBD分析:象例1一样构造三角形,利用解三角形求解。实例讲解解:测量者可以在河岸边选定两点C、D,测的CD=a
并且在C、D两点分别测得在三角形ADC和BDC中,应用正弦定理得计算出AC和BC后,再在三角形ABC中,应用余弦定理计算出AB两点间的距离: 思考题: 我舰在敌岛A南偏西 相距12 海里的B处,发现敌舰正由
岛北偏西 的方向以10海里的速度航行。问我舰需以多
大速度,沿什么方向航行才能用2小时追上敌舰?课堂小结1、本节课通过举例说明了解斜三角形在实际中的一些应用。
掌握利用正弦定理及余弦定理解任意三角形的方法。2、利用解三角形知识解应用题的一般步骤:分析建摸求解检验课后作业课本第14页练习1、2
解决有关测量距离的问题知识回顾1、正弦定理:2、余弦定理:二、应 用:一、定理内容:求三角形中的某些元素实例讲解分 析:在本题中直接给出了数学模型(三角形),要求A、B间距离,相当于在三角形中求某一边长?想一想例1、如下图,设A、B两点在河的两岸,要测量两点之间的距 离。测量者在A的同侧, 在所在的河岸边选定一点C,测出AC的距离是55 m,求点A、B两点间的距离(精确到0.1 m).用正弦定理或余弦定理解决实例讲解答:A、B两点的距离为65.7米.解:分析:用正弦定理解决,只须求出 进而求出边AB的长。如果对例1的题目进行修改:点A、B都在河的对岸
且不可到达,那又如何求A、B两点间的距离?请同
学们设计一种方法求A、B两点间的距离。(如图)实例讲解想一想ACBD分析:象例1一样构造三角形,利用解三角形求解。实例讲解解:测量者可以在河岸边选定两点C、D,测的CD=a
并且在C、D两点分别测得在三角形ADC和BDC中,应用正弦定理得计算出AC和BC后,再在三角形ABC中,应用余弦定理计算出AB两点间的距离: 思考题: 我舰在敌岛A南偏西 相距12 海里的B处,发现敌舰正由
岛北偏西 的方向以10海里的速度航行。问我舰需以多
大速度,沿什么方向航行才能用2小时追上敌舰?课堂小结1、本节课通过举例说明了解斜三角形在实际中的一些应用。
掌握利用正弦定理及余弦定理解任意三角形的方法。2、利用解三角形知识解应用题的一般步骤:分析建摸求解检验课后作业课本第14页练习1、2
