1.3.2有理数的减法 课件(共22张PPT)
文档属性
| 名称 | 1.3.2有理数的减法 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 680.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-07 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
第1.3.2 有理数的减法
人教版数学七年级上册
1.理解掌握有理数的减法法则,会进行有理数的减法运算;
2.理解加减法统一成加法的意义,能熟练地进行有理数加减法的混合运算;
3.通过加减法的相互转化,培养应变能力、计算能力.
学习目标
实际问题中有时还要涉及有理数的减法. 例如,本章引言中,北京某天的气温是- 3 ℃ 3 ℃,这天的温差(最高气温减最低气温,单位:℃)就是3 –(-3).这里遇到正数与负数的减法.
你能看出3 C比-3 C高多少摄氏度吗?
情境引入
减法是加法的逆运算,计算3-(-3),就是要求出一个数x,使得x与-3相加得3.
因为6与-3相加得3,所以x应该是6,即
3-(-3)=6 ①
另一方面,我们知道
3+(+3)=6 ②
由①②,有
3-(-3)=3+(+3) ③
互动新授
探究
从3-(-3)=3+(+3)能看出减-3相当加哪个数吗?把3换成0,-1,-5,用上面的方法考虑0-(-3),(-1)-(-3),(-5)-(-3).这些数减-3的结果与它们加+3的结果相同吗?
0-(-3)=0+3=3,(-1)-(-3)=(-1)+3=2,(-5)-(-3)=(-5)+3=-2
计算9-8,9+(-8);15-7,15+(-7).从中又能有什么发现吗?
9-8=1,9+(-8)=1,
15-7=8,15+(-7)=8,
所以9-8=9+(-8).
所以15-7=15+(-7).
互动新授
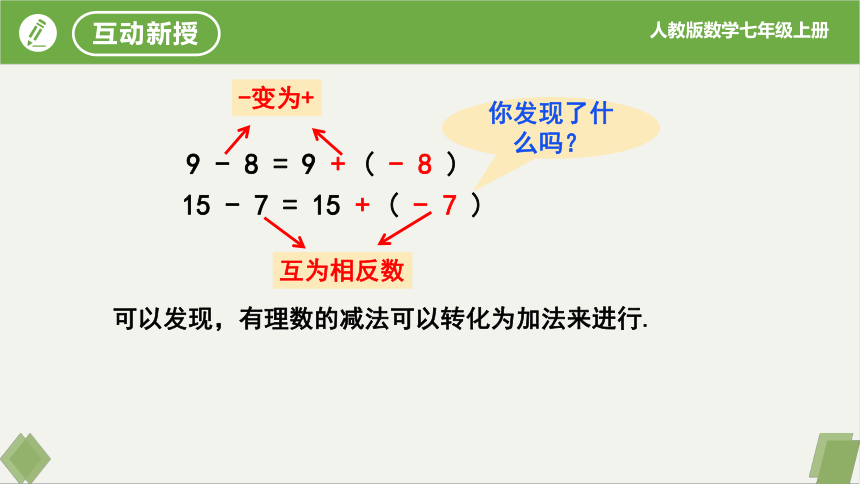
9 - 8 = 9 + ( - 8 )
15 - 7 = 15 + ( - 7 )
-变为+
互为相反数
你发现了什么吗?
可以发现,有理数的减法可以转化为加法来进行.
互动新授
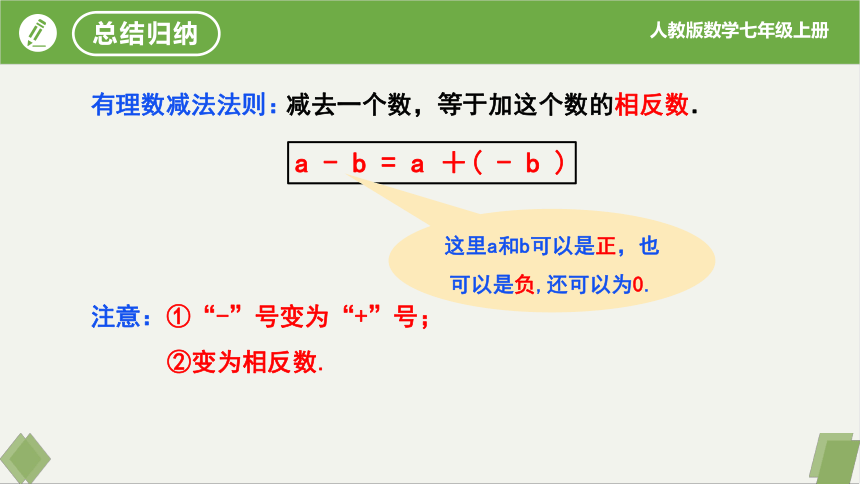
减去一个数,等于加这个数的相反数.
有理数减法法则:
a - b = a +( - b )
这里a和b可以是正,也可以是负,还可以为0.
注意:①“-”号变为“+”号;
②变为相反数.
总结归纳
例4 计算:(1)(-3)-(-5). (2)0-7.
(3)7.2-(-4.8). (4)
解:(1)(-3)-(-5)=(-3)+5=2;
(2)0-7=0+(-7)=-7;
(3)7.2-(-4.8)=7.2+4.8=12;
(4)
典例精析
当a≥b时,a-b≥0;
当a思考
在小学,只有当a大于或等于b时,我们才会做a-b(例如2-1,1-1).现在,当a小于b时,你会做a-b(例如1-2,(-1)-1)吗?
一般地,较小的数减较大的数,所得的差是_____数.
负
总结归纳
例5 计算:(-20)+(+3)-(-5)-(+7)
分析:这个算式中有加法,也有减法.可以根据有理数减法法则,把它改写为(-20)+(+3)+(+5)+(-7),
解:原式=(-20)+(+3)+(+5)+(-7)
=(-20)+(-7)+(+3)+(+5)
=[(-20)+(-7)]+[(+3)+(+5)]
=(-27)+(+8)
=-19
减法转化成加法
加法结合律
加法交换律
典例精析
要点归纳:引入相反数后,加减混合运算可以统一为加法运算:a+b-c=a+b+(-c).
算式-20)+(+3)+(+5)+(-7)是 , , , 这四个数的和.
为书写简单,省略算式中的括号和加号写为-20+3+5-7 我们可以读作 的和,或读作 加 加 减 .
负20、正3、正5、负7
负20 3 5 7
-20 3 5 -7
例5的运算过程可以简单写为(-20)+(+3)+(+5)+(-7)
=-20+3+5-7
=-20-7+3+5
=-19
互动新授
0
B
A
探究
在数轴上,点A、B分别表示数a,b ,利用有理数减法法则探究:点A、B之间的距离与a,b的关系.
结论:AB=|a-b|
互动新授
1.下列括号内各应填什么数
(1)(+3)-(-7)=(+3)+( );
(2)0 - (-9)= 0 +( );
(3)(-6)- 2 =(-6)+( );
(4)1 - (+12) = 1 +( )
+7
+9
-2
-12
小试牛刀
课堂检测
1.计算:
(1) 6-9 (2) (+4)-(-7) (3) (-5)-(-8)
(4) 0-(-5) (5) (-2.5)-5.9 (6) 1.9-(-0.6)
解:(1) 6-9=6+(-9)=-3 (2)(+4)-(-7)=4+7=11
(3)(-5)-(-8)=(-5)+8=3 (4)0-(-5)=0+5=5
(5)(-2.5)-5.9=(-2.5)+(-5.9)=-8.4
(6)1.9-(-0.6)=1.9+0.6=2.5
2、判断
(1)在有理数的加法中,两数的和一定比加数大( )
(2)两个数相减,被减数一定比减数大( )
(3)两数之差一定小于被减数( )
(4)0减去任何数,差都为负数( )
(5)较大的数减去较小的数,差一定是正数( )
√
×
×
×
×
课堂检测
3.计算:(1)25-18-(-9)+(-12);
解:原式=25-18+9-12
=(25+9)+(-18-12)
=34+(-30)
=4.
(2)(-21.5)+(-7.4)-17.5+7.4;
解:原式=(-21.5-17.5)+[(-7.4)+7.4]
=-39+0
=-39.
课堂检测
拓展训练
1.若=4,=2,且a+b的绝对值与相反数相等,则a-b的值是( )
A.-2 B.-6 C.-2或-6 D.2或6
2.若|a|=2,|b﹣2|=5,且|a+b|=a+b,则a﹣b的值是( )
A.5 B.5或9 C.﹣5 D.﹣5或﹣9
C
D
3.下列说法中错误的是( )
A.如果a>0,b<0且a+b>0,则|a|>|b|
B.如果a<0,b>0,则a-b<0
C.如果a+b<0,且a,b同号,那么a>0,b>0
D.如果a<0,b<0且|a|>|b|,则a-b<0
4.若=3,=5,且a+b<0,那么a-b的值是( )
A.2或8 B.-2或-8 C.3或7 D.2或-2
A
C
拓展训练
有理数加减混合运算的步骤:
(1)将减法转化为加法运算;
(2)省略加号和括号;
(3)运用加法交换律和结合律,将同号两数相加;
(4)按有理数加法法则计算.
减去一个数,等于加这个数的相反数.
有理数减法法则:
a - b = a +( - b )
课堂小结
课后作业
1.计算:
(1)(-3.5)-(-7) (2)(-1.6)-3.2 (3)0-(-2.7)
解(1)(-3.5)-(-7) (2)(-1.6)-3.2 (3)0-(-2.7)
=(-3.5)+7 =(-1.6)+(-3.2) =0+2.7
=3.5 =-4.8 =2.7
2.小明计划在假期每天做5道数学题,超过的题数记为正数,不足的题数记为负数.他十天中做的题数记录如下:3,5,4,2,-1,7,0,-3,8,10,则小明这十天共做了多少道数学题?
解:3+5+(-4)+2+(-1)+7+0+(-3)+8+10
=(3+5+2+7+0+8+10)+[(-4)+(-1)+(-3)]
=35+(-8)=27,5×10+27=77(道).
答:小明这十天共做了77道数学题.
课后作业
谢谢聆听
第1.3.2 有理数的减法
人教版数学七年级上册
1.理解掌握有理数的减法法则,会进行有理数的减法运算;
2.理解加减法统一成加法的意义,能熟练地进行有理数加减法的混合运算;
3.通过加减法的相互转化,培养应变能力、计算能力.
学习目标
实际问题中有时还要涉及有理数的减法. 例如,本章引言中,北京某天的气温是- 3 ℃ 3 ℃,这天的温差(最高气温减最低气温,单位:℃)就是3 –(-3).这里遇到正数与负数的减法.
你能看出3 C比-3 C高多少摄氏度吗?
情境引入
减法是加法的逆运算,计算3-(-3),就是要求出一个数x,使得x与-3相加得3.
因为6与-3相加得3,所以x应该是6,即
3-(-3)=6 ①
另一方面,我们知道
3+(+3)=6 ②
由①②,有
3-(-3)=3+(+3) ③
互动新授
探究
从3-(-3)=3+(+3)能看出减-3相当加哪个数吗?把3换成0,-1,-5,用上面的方法考虑0-(-3),(-1)-(-3),(-5)-(-3).这些数减-3的结果与它们加+3的结果相同吗?
0-(-3)=0+3=3,(-1)-(-3)=(-1)+3=2,(-5)-(-3)=(-5)+3=-2
计算9-8,9+(-8);15-7,15+(-7).从中又能有什么发现吗?
9-8=1,9+(-8)=1,
15-7=8,15+(-7)=8,
所以9-8=9+(-8).
所以15-7=15+(-7).
互动新授
9 - 8 = 9 + ( - 8 )
15 - 7 = 15 + ( - 7 )
-变为+
互为相反数
你发现了什么吗?
可以发现,有理数的减法可以转化为加法来进行.
互动新授
减去一个数,等于加这个数的相反数.
有理数减法法则:
a - b = a +( - b )
这里a和b可以是正,也可以是负,还可以为0.
注意:①“-”号变为“+”号;
②变为相反数.
总结归纳
例4 计算:(1)(-3)-(-5). (2)0-7.
(3)7.2-(-4.8). (4)
解:(1)(-3)-(-5)=(-3)+5=2;
(2)0-7=0+(-7)=-7;
(3)7.2-(-4.8)=7.2+4.8=12;
(4)
典例精析
当a≥b时,a-b≥0;
当a
在小学,只有当a大于或等于b时,我们才会做a-b(例如2-1,1-1).现在,当a小于b时,你会做a-b(例如1-2,(-1)-1)吗?
一般地,较小的数减较大的数,所得的差是_____数.
负
总结归纳
例5 计算:(-20)+(+3)-(-5)-(+7)
分析:这个算式中有加法,也有减法.可以根据有理数减法法则,把它改写为(-20)+(+3)+(+5)+(-7),
解:原式=(-20)+(+3)+(+5)+(-7)
=(-20)+(-7)+(+3)+(+5)
=[(-20)+(-7)]+[(+3)+(+5)]
=(-27)+(+8)
=-19
减法转化成加法
加法结合律
加法交换律
典例精析
要点归纳:引入相反数后,加减混合运算可以统一为加法运算:a+b-c=a+b+(-c).
算式-20)+(+3)+(+5)+(-7)是 , , , 这四个数的和.
为书写简单,省略算式中的括号和加号写为-20+3+5-7 我们可以读作 的和,或读作 加 加 减 .
负20、正3、正5、负7
负20 3 5 7
-20 3 5 -7
例5的运算过程可以简单写为(-20)+(+3)+(+5)+(-7)
=-20+3+5-7
=-20-7+3+5
=-19
互动新授
0
B
A
探究
在数轴上,点A、B分别表示数a,b ,利用有理数减法法则探究:点A、B之间的距离与a,b的关系.
结论:AB=|a-b|
互动新授
1.下列括号内各应填什么数
(1)(+3)-(-7)=(+3)+( );
(2)0 - (-9)= 0 +( );
(3)(-6)- 2 =(-6)+( );
(4)1 - (+12) = 1 +( )
+7
+9
-2
-12
小试牛刀
课堂检测
1.计算:
(1) 6-9 (2) (+4)-(-7) (3) (-5)-(-8)
(4) 0-(-5) (5) (-2.5)-5.9 (6) 1.9-(-0.6)
解:(1) 6-9=6+(-9)=-3 (2)(+4)-(-7)=4+7=11
(3)(-5)-(-8)=(-5)+8=3 (4)0-(-5)=0+5=5
(5)(-2.5)-5.9=(-2.5)+(-5.9)=-8.4
(6)1.9-(-0.6)=1.9+0.6=2.5
2、判断
(1)在有理数的加法中,两数的和一定比加数大( )
(2)两个数相减,被减数一定比减数大( )
(3)两数之差一定小于被减数( )
(4)0减去任何数,差都为负数( )
(5)较大的数减去较小的数,差一定是正数( )
√
×
×
×
×
课堂检测
3.计算:(1)25-18-(-9)+(-12);
解:原式=25-18+9-12
=(25+9)+(-18-12)
=34+(-30)
=4.
(2)(-21.5)+(-7.4)-17.5+7.4;
解:原式=(-21.5-17.5)+[(-7.4)+7.4]
=-39+0
=-39.
课堂检测
拓展训练
1.若=4,=2,且a+b的绝对值与相反数相等,则a-b的值是( )
A.-2 B.-6 C.-2或-6 D.2或6
2.若|a|=2,|b﹣2|=5,且|a+b|=a+b,则a﹣b的值是( )
A.5 B.5或9 C.﹣5 D.﹣5或﹣9
C
D
3.下列说法中错误的是( )
A.如果a>0,b<0且a+b>0,则|a|>|b|
B.如果a<0,b>0,则a-b<0
C.如果a+b<0,且a,b同号,那么a>0,b>0
D.如果a<0,b<0且|a|>|b|,则a-b<0
4.若=3,=5,且a+b<0,那么a-b的值是( )
A.2或8 B.-2或-8 C.3或7 D.2或-2
A
C
拓展训练
有理数加减混合运算的步骤:
(1)将减法转化为加法运算;
(2)省略加号和括号;
(3)运用加法交换律和结合律,将同号两数相加;
(4)按有理数加法法则计算.
减去一个数,等于加这个数的相反数.
有理数减法法则:
a - b = a +( - b )
课堂小结
课后作业
1.计算:
(1)(-3.5)-(-7) (2)(-1.6)-3.2 (3)0-(-2.7)
解(1)(-3.5)-(-7) (2)(-1.6)-3.2 (3)0-(-2.7)
=(-3.5)+7 =(-1.6)+(-3.2) =0+2.7
=3.5 =-4.8 =2.7
2.小明计划在假期每天做5道数学题,超过的题数记为正数,不足的题数记为负数.他十天中做的题数记录如下:3,5,4,2,-1,7,0,-3,8,10,则小明这十天共做了多少道数学题?
解:3+5+(-4)+2+(-1)+7+0+(-3)+8+10
=(3+5+2+7+0+8+10)+[(-4)+(-1)+(-3)]
=35+(-8)=27,5×10+27=77(道).
答:小明这十天共做了77道数学题.
课后作业
谢谢聆听
