2.3 确定圆的条件 课件(共36张PPT)
文档属性
| 名称 | 2.3 确定圆的条件 课件(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 35.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-07 08:34:44 | ||
图片预览







文档简介
(共36张PPT)
2.3 确定圆的条件
第2章对称图形——圆
教学目标
01
探究确定圆的条件,理解不在同一条直线上的三点确定一个圆的充分性
02
理解三角形的外接圆、三角形的外心、圆的内接三角形的概念,能够熟练地作出一个三角形的外接圆
确定圆的条件
01
二、定义
复习引入
回顾1:(1)过一点可以作几条直线?
无数条
01
二、定义
复习引入
(2)过两点可以作几条直线?
有且只有一条【两点确定一条直线】
既然点可以作为确定直线的条件,
那么是否也可以作为确定圆的条件呢?
01
二、定义
复习引入
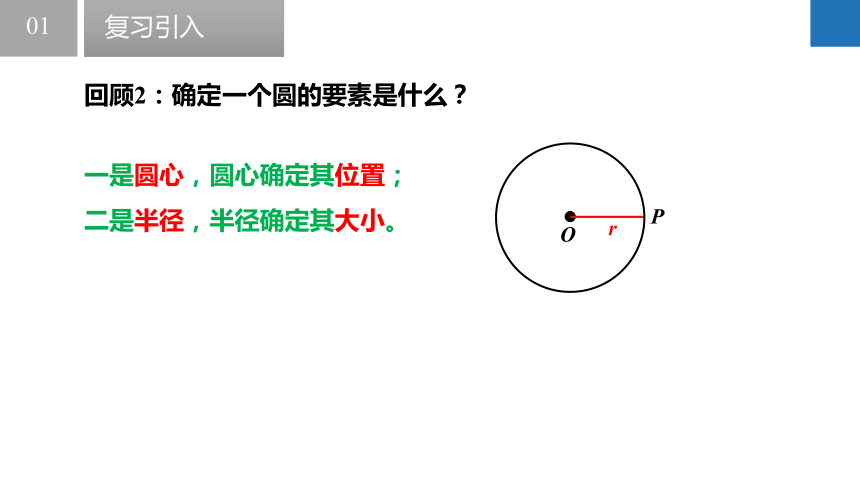
回顾2:确定一个圆的要素是什么?
一是圆心,圆心确定其位置;
二是半径,半径确定其大小。
O
P
r
01
二、定义
情境引入
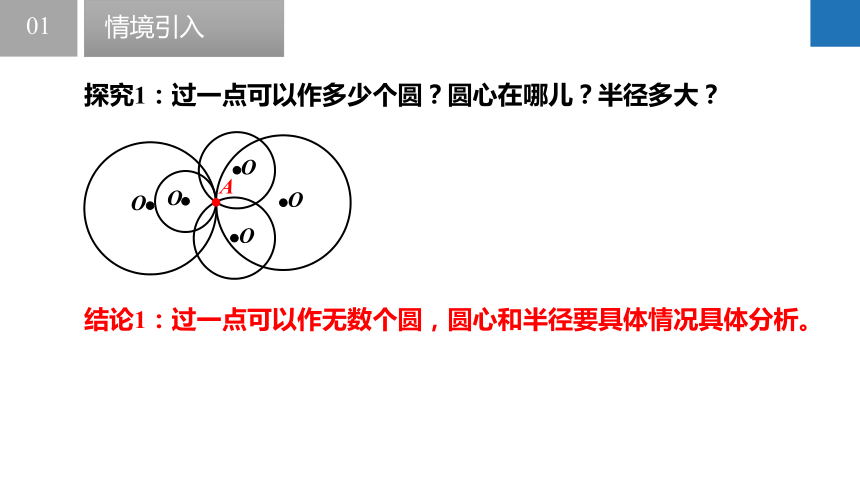
探究1:过一点可以作多少个圆?圆心在哪儿?半径多大?
结论1:过一点可以作无数个圆,圆心和半径要具体情况具体分析。
O
O
O
O
O
A
01
二、定义
情境引入
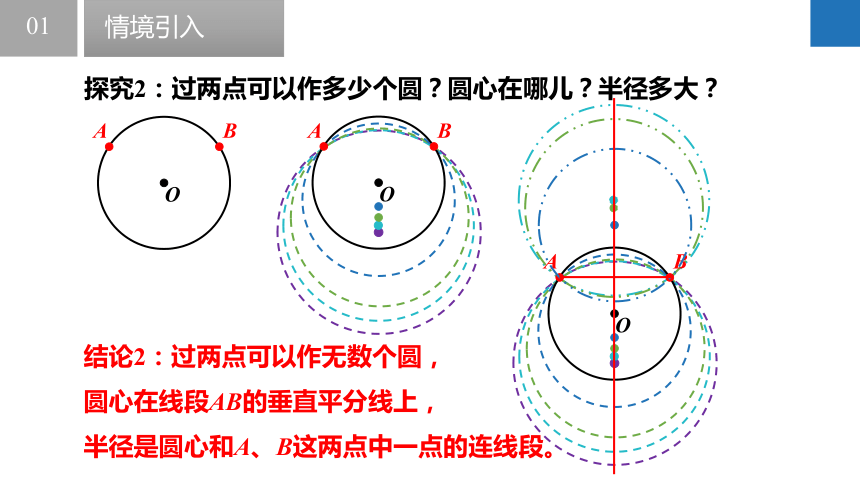
探究2:过两点可以作多少个圆?圆心在哪儿?半径多大?
O
A
B
O
A
B
O
A
B
结论2:过两点可以作无数个圆,
圆心在线段AB的垂直平分线上,
半径是圆心和A、B这两点中一点的连线段。
01
二、定义
情境引入
探究3:过三点可以作多少个圆?圆心在哪儿?半径多大?
设三点分别为A、B、C,且假设过这三点可以作圆,
那么圆心应在AB的垂直平分线l1上,又在BC的垂直平分线l2上。
l1与l2可能平行,也可能相交。
01
二、定义
情境引入
A
B
C
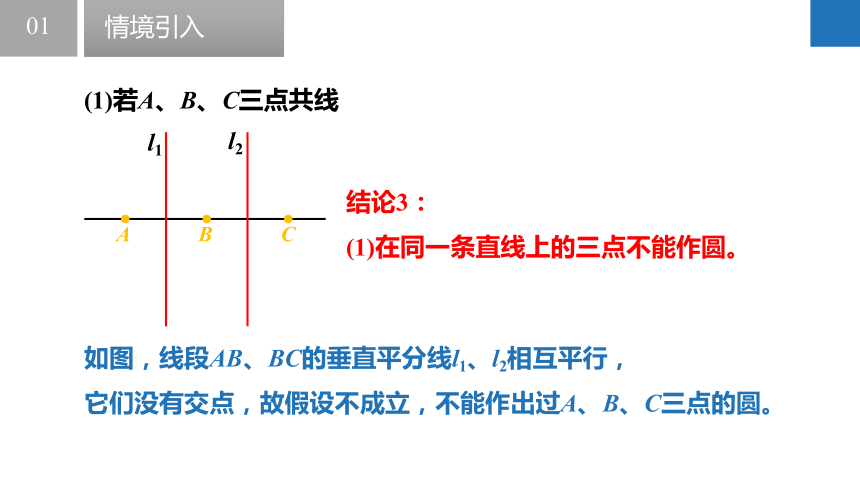
(1)若A、B、C三点共线
l1
l2
结论3:
(1)在同一条直线上的三点不能作圆。
如图,线段AB、BC的垂直平分线l1、l2相互平行,
它们没有交点,故假设不成立,不能作出过A、B、C三点的圆。
01
二、定义
情境引入
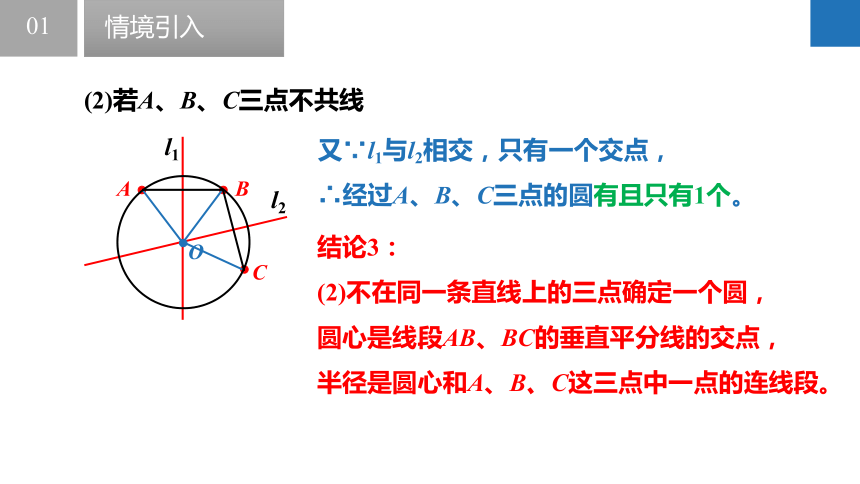
(2)若A、B、C三点不共线
如图,l1与l2相交。
A
B
C
l1
l2
设l1与l2的交点为O——即圆心;
O
∵OA=OB=OC,
∴连接OA(或OB、OC)——即半径。
∴以点O为圆心,OA为半径的圆经过A、B、C三点
01
二、定义
情境引入
(2)若A、B、C三点不共线
又∵l1与l2相交,只有一个交点,
∴经过A、B、C三点的圆有且只有1个。
结论3:
(2)不在同一条直线上的三点确定一个圆,
圆心是线段AB、BC的垂直平分线的交点,
半径是圆心和A、B、C这三点中一点的连线段。
A
B
C
l1
l2
O
02
二、定义
知识精讲
确定圆的条件
不在同一条直线上的三点确定一个圆。
A
B
C
l1
l2
O
例1、下列条件中,不能确定一个圆的是( )
A.圆心与半径
B.直径
C.平面上的三个已知点
D.三角形的三个顶点
03
典例精析
C
不在同一条直线上的三点确定一个圆。
例2、如图,点A,B,C,D均在直线l上,点P在直线l外,则经过其中任意三个点,最多可画出圆的个数为( )
A.3个 B.4个 C.5个 D.6个
03
典例精析
D
例3、已知直线a和直线外的两点A、B,经过A、B作一圆,使它的圆心在直线a上.
03
典例精析
例4、如图,在平面直角坐标系xOy中,点A,B,C的横、纵坐标都为整数,过这三个点作一条圆弧,则此圆弧的圆心坐标为________.
03
典例精析
(2,1)
解:从图形可知:A点的坐标是(0,2),
B点的坐标是(1,3),C点的坐标是(3,3),
如图,连接AB,
作线段AB和线段BC的垂直平分线MN、EF,两线交于Q,则Q是圆弧的圆心。
三角形的外接圆
与圆心
01
二、定义
情境引入
【思考与操作1】将不在同一条直线上的三点分别连接,你发现了什么?
不在同一条直线上的三点可以确定一个三角形
A
B
C
01
二、定义
情境引入
【思考与操作2】将过这三点确定的圆和三角形放在一个图形里
不在同一条直线上的三点确定一个圆,
即三角形的三个顶点确定一个圆。
A
B
C
O
02
二、定义
知识精讲
三角形的外接圆与外心
三角形的三个顶点确定一个圆,这个圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心。
这个三角形叫做圆的内接三角形。
A
B
C
O
eg:如图,O是△ABC的外接圆,△ABC是O的内接三角形。
02
二、定义
知识精讲
确定圆的条件
小明老师有几个问题想问问大家
Q1:已知△ABC,怎样用直尺和圆规确定三角形的外心(外接圆的圆心)?
A
B
C
分别作边AB、BC的垂直平分线l1、l2,l1与l2的交点为O。
l1
l2
O
作图
02
二、定义
知识精讲
确定圆的条件
Q2:如何确定三角形的外接圆的半径?
连接OA(或OB、OC)。
A
B
C
l1
l2
O
02
二、定义
知识精讲
确定圆的条件
Q3:如何作三角形的外接圆?
A
B
C
l1
l2
O
以点O为圆心,OA为半径作圆,O就是所求作的圆。
02
二、定义
知识精讲
确定圆的条件
三角形外接圆的作图步骤总结~
三角形的外心
作图
尺、规作三角形的外接圆 1、定圆心 分别作三角形任意两边的垂直平分线,两条线的交点为圆心
2、定半径 连接圆心和三角形的任意一个顶点,连线段为半径
3、定圆 以圆心、半径画圆
02
二、定义
知识精讲
确定圆的条件
进一步解读三角形的外心(外接圆的圆心)~
三角形的外心
A
B
C
l1
l2
O
A
B
C
l1
l2
O
三角形的外心 定义 三角形外接圆的圆心
作图 三角形三边垂直平分线的交点
性质 到三角形三个顶点的距离相等
三角形的外心 定义 三角形外接圆的圆心
作图
性质
三角形的外心 定义 三角形外接圆的圆心
作图 三角形三边垂直平分线的交点
性质
三角形的外心 定义 三角形外接圆的圆心
作图 三角形三边垂直平分线的交点
性质 到三角形三个顶点的距离相等
注意:外心到三角形三个顶点的距离相等,不是到三角形三边的距离相等。
02
二、定义
知识精讲
确定圆的条件
锐角、直角、钝角三角形的外心位置有何特点?
三角形的外心
A
B
C
O
锐角三角形的外心在三角形内;
A
B
C
O
直角三角形的外心位于直角三角形斜边中点,
此时,外接圆的半径为直角三角形斜边长的一半;
02
二、定义
知识精讲
确定圆的条件
三角形的外心
A
B
C
O
钝角三角形的外心在三角形外。
三角形的外心位置 锐角三角形 三角形内
直角三角形 直角三角形斜边中点
锐角三角形 三角形外
02
二、定义
知识精讲
确定圆的条件
进一步探究三角形的外接圆与圆的内接三角形的个数~
三角形的外接圆与圆的内接三角形
【思考】
(1)一个三角形的外接圆有几个?
∵不在同一条直线上的三点确定一个圆,
∴一个三角形的外接圆有且只有1个。
02
二、定义
知识精讲
确定圆的条件
三角形的外接圆与圆的内接三角形
【思考】
(2)一个圆的内接三角形有几个?
如图,
∵连接圆上任意三点即可以确定一个三角形,
∴一个圆的内接三角形有无数个。
一个三角形的外接圆有且只有1个,一个圆的内接三角形有无数个。
例1、公园的A,B,C处分别有海盗船、摩天轮、旋转木马三个娱乐项目,现要在公园内一个售票中心,使三个娱乐项目所处位置到售票中心的距离相等,则售票中心应建立在( )
A.△ABC三边高线的交点处
B.△ABC三角角平分线的交点处
C.△ABC三边中线的交点处
D.△ABC三边垂直平分线的交点处
03
典例精析
D
例2、如图,在平面直角坐标系xOy中,点A为(0,3),点B为(2,1),点C为(2,-3).则经画图操作可知:△ABC的外心坐标应是________.
03
典例精析
(-2,-1)
解:∵△ABC的外心即是三角形三边垂直平分线的交点,
∴如图,作边AB和边BC的垂直平分线MN、EF,两线交于O′,则O′是△ABC的外心。
例3、在Rt△ABC中,∠C=90°,AC=3,AB=4.则△ABC外接圆半径R=________.
03
典例精析
2
解:在Rt△ABC中,∠C=90°,AC=3,AB=4,
∴Rt△ABC的外接圆的半径为斜边长的一半=×4=2。
例4、下列说法正确的是( )
A.三点确定一个圆
B.三角形的外心到三角形三边的距离相等
C.平分弦的直径垂直于弦
D.垂直于弦且过圆心的直线平分这条弦
03
典例精析
D
注意:外心到三角形三个顶点的距离相等,不是到三角形三边的距离相等。
平分弦(不是直径)的直径垂直于弦。
例5、下列说法:①任意一个圆有且仅有一个内接三角形;②任意一个三角形有且仅有一个外接圆;③长度相等的两条弧是等弧;④直径是圆中最长的弦,其中正确的是( )
A.①③ B.①④ C.②③ D.②④
03
典例精析
D
注意:在同圆或等圆中,长度相等的两条弧是等弧。
一个三角形的外接圆有且只有1个,一个圆的内接三角形有无数个。
课后总结
不在同一条直线上的三点确定一个圆。
三角形的三个顶点确定一个圆,这个圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心。
这个三角形叫做圆的内接三角形。
三角形的外心 定义 三角形外接圆的圆心
作图 三角形三边垂直平分线的交点
性质 到三角形三个顶点的距离相等
注意:不是到三角形三边的距离相等
三角形的外心位置 锐角三角形 三角形内
直角三角形 直角三角形斜边中点
锐角三角形 三角形外
一个三角形的外接圆有且只有1个,一个圆的内接三角形有无数个。
尺、规作三角形的外接圆 1、定圆心 分别作三角形任意两边的垂直平分线,两条线的交点为圆心
2、定半径 连接圆心和三角形的任意一个顶点,连线段为半径
3、定圆 以圆心、半径画圆
2.3 确定圆的条件
第2章对称图形——圆
教学目标
01
探究确定圆的条件,理解不在同一条直线上的三点确定一个圆的充分性
02
理解三角形的外接圆、三角形的外心、圆的内接三角形的概念,能够熟练地作出一个三角形的外接圆
确定圆的条件
01
二、定义
复习引入
回顾1:(1)过一点可以作几条直线?
无数条
01
二、定义
复习引入
(2)过两点可以作几条直线?
有且只有一条【两点确定一条直线】
既然点可以作为确定直线的条件,
那么是否也可以作为确定圆的条件呢?
01
二、定义
复习引入
回顾2:确定一个圆的要素是什么?
一是圆心,圆心确定其位置;
二是半径,半径确定其大小。
O
P
r
01
二、定义
情境引入
探究1:过一点可以作多少个圆?圆心在哪儿?半径多大?
结论1:过一点可以作无数个圆,圆心和半径要具体情况具体分析。
O
O
O
O
O
A
01
二、定义
情境引入
探究2:过两点可以作多少个圆?圆心在哪儿?半径多大?
O
A
B
O
A
B
O
A
B
结论2:过两点可以作无数个圆,
圆心在线段AB的垂直平分线上,
半径是圆心和A、B这两点中一点的连线段。
01
二、定义
情境引入
探究3:过三点可以作多少个圆?圆心在哪儿?半径多大?
设三点分别为A、B、C,且假设过这三点可以作圆,
那么圆心应在AB的垂直平分线l1上,又在BC的垂直平分线l2上。
l1与l2可能平行,也可能相交。
01
二、定义
情境引入
A
B
C
(1)若A、B、C三点共线
l1
l2
结论3:
(1)在同一条直线上的三点不能作圆。
如图,线段AB、BC的垂直平分线l1、l2相互平行,
它们没有交点,故假设不成立,不能作出过A、B、C三点的圆。
01
二、定义
情境引入
(2)若A、B、C三点不共线
如图,l1与l2相交。
A
B
C
l1
l2
设l1与l2的交点为O——即圆心;
O
∵OA=OB=OC,
∴连接OA(或OB、OC)——即半径。
∴以点O为圆心,OA为半径的圆经过A、B、C三点
01
二、定义
情境引入
(2)若A、B、C三点不共线
又∵l1与l2相交,只有一个交点,
∴经过A、B、C三点的圆有且只有1个。
结论3:
(2)不在同一条直线上的三点确定一个圆,
圆心是线段AB、BC的垂直平分线的交点,
半径是圆心和A、B、C这三点中一点的连线段。
A
B
C
l1
l2
O
02
二、定义
知识精讲
确定圆的条件
不在同一条直线上的三点确定一个圆。
A
B
C
l1
l2
O
例1、下列条件中,不能确定一个圆的是( )
A.圆心与半径
B.直径
C.平面上的三个已知点
D.三角形的三个顶点
03
典例精析
C
不在同一条直线上的三点确定一个圆。
例2、如图,点A,B,C,D均在直线l上,点P在直线l外,则经过其中任意三个点,最多可画出圆的个数为( )
A.3个 B.4个 C.5个 D.6个
03
典例精析
D
例3、已知直线a和直线外的两点A、B,经过A、B作一圆,使它的圆心在直线a上.
03
典例精析
例4、如图,在平面直角坐标系xOy中,点A,B,C的横、纵坐标都为整数,过这三个点作一条圆弧,则此圆弧的圆心坐标为________.
03
典例精析
(2,1)
解:从图形可知:A点的坐标是(0,2),
B点的坐标是(1,3),C点的坐标是(3,3),
如图,连接AB,
作线段AB和线段BC的垂直平分线MN、EF,两线交于Q,则Q是圆弧的圆心。
三角形的外接圆
与圆心
01
二、定义
情境引入
【思考与操作1】将不在同一条直线上的三点分别连接,你发现了什么?
不在同一条直线上的三点可以确定一个三角形
A
B
C
01
二、定义
情境引入
【思考与操作2】将过这三点确定的圆和三角形放在一个图形里
不在同一条直线上的三点确定一个圆,
即三角形的三个顶点确定一个圆。
A
B
C
O
02
二、定义
知识精讲
三角形的外接圆与外心
三角形的三个顶点确定一个圆,这个圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心。
这个三角形叫做圆的内接三角形。
A
B
C
O
eg:如图,O是△ABC的外接圆,△ABC是O的内接三角形。
02
二、定义
知识精讲
确定圆的条件
小明老师有几个问题想问问大家
Q1:已知△ABC,怎样用直尺和圆规确定三角形的外心(外接圆的圆心)?
A
B
C
分别作边AB、BC的垂直平分线l1、l2,l1与l2的交点为O。
l1
l2
O
作图
02
二、定义
知识精讲
确定圆的条件
Q2:如何确定三角形的外接圆的半径?
连接OA(或OB、OC)。
A
B
C
l1
l2
O
02
二、定义
知识精讲
确定圆的条件
Q3:如何作三角形的外接圆?
A
B
C
l1
l2
O
以点O为圆心,OA为半径作圆,O就是所求作的圆。
02
二、定义
知识精讲
确定圆的条件
三角形外接圆的作图步骤总结~
三角形的外心
作图
尺、规作三角形的外接圆 1、定圆心 分别作三角形任意两边的垂直平分线,两条线的交点为圆心
2、定半径 连接圆心和三角形的任意一个顶点,连线段为半径
3、定圆 以圆心、半径画圆
02
二、定义
知识精讲
确定圆的条件
进一步解读三角形的外心(外接圆的圆心)~
三角形的外心
A
B
C
l1
l2
O
A
B
C
l1
l2
O
三角形的外心 定义 三角形外接圆的圆心
作图 三角形三边垂直平分线的交点
性质 到三角形三个顶点的距离相等
三角形的外心 定义 三角形外接圆的圆心
作图
性质
三角形的外心 定义 三角形外接圆的圆心
作图 三角形三边垂直平分线的交点
性质
三角形的外心 定义 三角形外接圆的圆心
作图 三角形三边垂直平分线的交点
性质 到三角形三个顶点的距离相等
注意:外心到三角形三个顶点的距离相等,不是到三角形三边的距离相等。
02
二、定义
知识精讲
确定圆的条件
锐角、直角、钝角三角形的外心位置有何特点?
三角形的外心
A
B
C
O
锐角三角形的外心在三角形内;
A
B
C
O
直角三角形的外心位于直角三角形斜边中点,
此时,外接圆的半径为直角三角形斜边长的一半;
02
二、定义
知识精讲
确定圆的条件
三角形的外心
A
B
C
O
钝角三角形的外心在三角形外。
三角形的外心位置 锐角三角形 三角形内
直角三角形 直角三角形斜边中点
锐角三角形 三角形外
02
二、定义
知识精讲
确定圆的条件
进一步探究三角形的外接圆与圆的内接三角形的个数~
三角形的外接圆与圆的内接三角形
【思考】
(1)一个三角形的外接圆有几个?
∵不在同一条直线上的三点确定一个圆,
∴一个三角形的外接圆有且只有1个。
02
二、定义
知识精讲
确定圆的条件
三角形的外接圆与圆的内接三角形
【思考】
(2)一个圆的内接三角形有几个?
如图,
∵连接圆上任意三点即可以确定一个三角形,
∴一个圆的内接三角形有无数个。
一个三角形的外接圆有且只有1个,一个圆的内接三角形有无数个。
例1、公园的A,B,C处分别有海盗船、摩天轮、旋转木马三个娱乐项目,现要在公园内一个售票中心,使三个娱乐项目所处位置到售票中心的距离相等,则售票中心应建立在( )
A.△ABC三边高线的交点处
B.△ABC三角角平分线的交点处
C.△ABC三边中线的交点处
D.△ABC三边垂直平分线的交点处
03
典例精析
D
例2、如图,在平面直角坐标系xOy中,点A为(0,3),点B为(2,1),点C为(2,-3).则经画图操作可知:△ABC的外心坐标应是________.
03
典例精析
(-2,-1)
解:∵△ABC的外心即是三角形三边垂直平分线的交点,
∴如图,作边AB和边BC的垂直平分线MN、EF,两线交于O′,则O′是△ABC的外心。
例3、在Rt△ABC中,∠C=90°,AC=3,AB=4.则△ABC外接圆半径R=________.
03
典例精析
2
解:在Rt△ABC中,∠C=90°,AC=3,AB=4,
∴Rt△ABC的外接圆的半径为斜边长的一半=×4=2。
例4、下列说法正确的是( )
A.三点确定一个圆
B.三角形的外心到三角形三边的距离相等
C.平分弦的直径垂直于弦
D.垂直于弦且过圆心的直线平分这条弦
03
典例精析
D
注意:外心到三角形三个顶点的距离相等,不是到三角形三边的距离相等。
平分弦(不是直径)的直径垂直于弦。
例5、下列说法:①任意一个圆有且仅有一个内接三角形;②任意一个三角形有且仅有一个外接圆;③长度相等的两条弧是等弧;④直径是圆中最长的弦,其中正确的是( )
A.①③ B.①④ C.②③ D.②④
03
典例精析
D
注意:在同圆或等圆中,长度相等的两条弧是等弧。
一个三角形的外接圆有且只有1个,一个圆的内接三角形有无数个。
课后总结
不在同一条直线上的三点确定一个圆。
三角形的三个顶点确定一个圆,这个圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心。
这个三角形叫做圆的内接三角形。
三角形的外心 定义 三角形外接圆的圆心
作图 三角形三边垂直平分线的交点
性质 到三角形三个顶点的距离相等
注意:不是到三角形三边的距离相等
三角形的外心位置 锐角三角形 三角形内
直角三角形 直角三角形斜边中点
锐角三角形 三角形外
一个三角形的外接圆有且只有1个,一个圆的内接三角形有无数个。
尺、规作三角形的外接圆 1、定圆心 分别作三角形任意两边的垂直平分线,两条线的交点为圆心
2、定半径 连接圆心和三角形的任意一个顶点,连线段为半径
3、定圆 以圆心、半径画圆
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
