数学 北师大版 九年级上册第一章2 矩形的性质与判定同步测试(含答案)
文档属性
| 名称 | 数学 北师大版 九年级上册第一章2 矩形的性质与判定同步测试(含答案) | 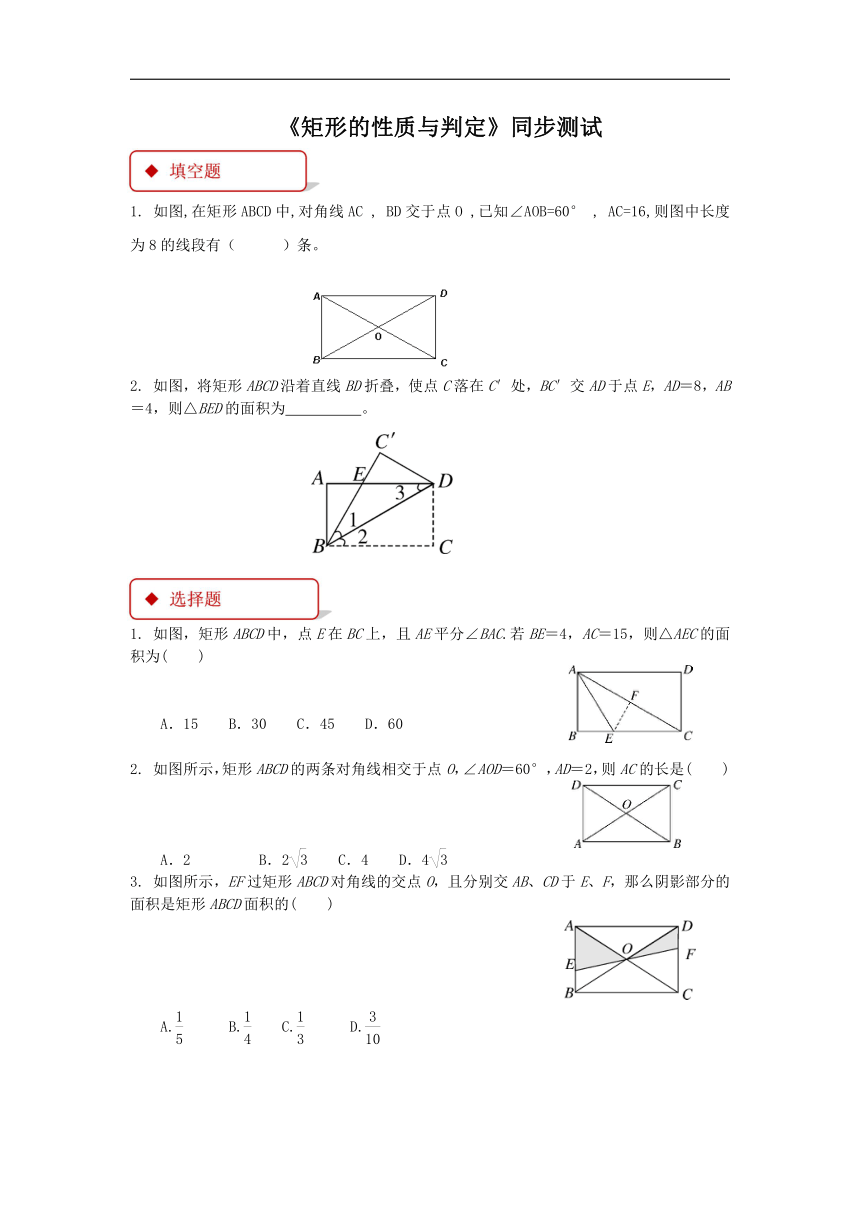 | |
| 格式 | docx | ||
| 文件大小 | 46.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-22 16:26:45 | ||
图片预览

文档简介
《矩形的性质与判定》同步测试
1. 如图,在矩形ABCD中,对角线AC , BD交于点O ,已知∠AOB=60° , AC=16,则图中长度为8的线段有( )条。
2. 如图,将矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于点E,AD=8,AB=4,则△BED的面积为 。
1. 如图,矩形ABCD中,点E在BC上,且AE平分∠BAC.若BE=4,AC=15,则△AEC的面积为( )
A.15 B.30 C.45 D.60
2. 如图所示,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=2,则AC的长是( )
A.2 B.2 C.4 D.4
3. 如图所示,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD面积的( )
A. B. C. D.
1. 如图,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm,矩形ABCD的周长为32cm,求AE的长。
2. 如图,在矩形ABCD中,AE⊥BD于E,∠DAE:∠BAE=3:1,求∠BAE和∠EAO的度数。
答案与解析
1. 4
2. 10
1. B 2. C 3. B
1. 解:∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴∠CED+∠ECD=90°。
又∵EF⊥EC,
∴∠AEF+∠CED=90°,
∴∠AEF=∠ECD。
而EF=EC,
∴△AEF≌△DCE,
∴AE=CD。
设AE=xcm,
∴CD=xcm,AD=(x+4)cm,
则有x+4+x=16,解得x=6。
即AE的长为6cm。
2. 解:∵四边形ABCD是矩形,∴∠DAB=90°,
AO=AC,BO=BD,AC=BD,
∴∠BAE+∠DAE=90°,AO=BO。
又∵∠DAE:∠BAE=3:1,
∴∠BAE=22.5°,∠DAE=67.5°。
∵AE⊥BD,
∴∠ABE=90°-∠BAE=90°-22.5°=67.5°,
∴∠OAB=∠ABE=67.5°
∴∠EAO=67.5°-22.5°=45°。
1. 如图,在矩形ABCD中,对角线AC , BD交于点O ,已知∠AOB=60° , AC=16,则图中长度为8的线段有( )条。
2. 如图,将矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于点E,AD=8,AB=4,则△BED的面积为 。
1. 如图,矩形ABCD中,点E在BC上,且AE平分∠BAC.若BE=4,AC=15,则△AEC的面积为( )
A.15 B.30 C.45 D.60
2. 如图所示,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=2,则AC的长是( )
A.2 B.2 C.4 D.4
3. 如图所示,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD面积的( )
A. B. C. D.
1. 如图,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm,矩形ABCD的周长为32cm,求AE的长。
2. 如图,在矩形ABCD中,AE⊥BD于E,∠DAE:∠BAE=3:1,求∠BAE和∠EAO的度数。
答案与解析
1. 4
2. 10
1. B 2. C 3. B
1. 解:∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴∠CED+∠ECD=90°。
又∵EF⊥EC,
∴∠AEF+∠CED=90°,
∴∠AEF=∠ECD。
而EF=EC,
∴△AEF≌△DCE,
∴AE=CD。
设AE=xcm,
∴CD=xcm,AD=(x+4)cm,
则有x+4+x=16,解得x=6。
即AE的长为6cm。
2. 解:∵四边形ABCD是矩形,∴∠DAB=90°,
AO=AC,BO=BD,AC=BD,
∴∠BAE+∠DAE=90°,AO=BO。
又∵∠DAE:∠BAE=3:1,
∴∠BAE=22.5°,∠DAE=67.5°。
∵AE⊥BD,
∴∠ABE=90°-∠BAE=90°-22.5°=67.5°,
∴∠OAB=∠ABE=67.5°
∴∠EAO=67.5°-22.5°=45°。
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
