数学 北师大版 九年级上册 第四章 5相似三角形的判定第1课时同步测试(含答案)
文档属性
| 名称 | 数学 北师大版 九年级上册 第四章 5相似三角形的判定第1课时同步测试(含答案) | 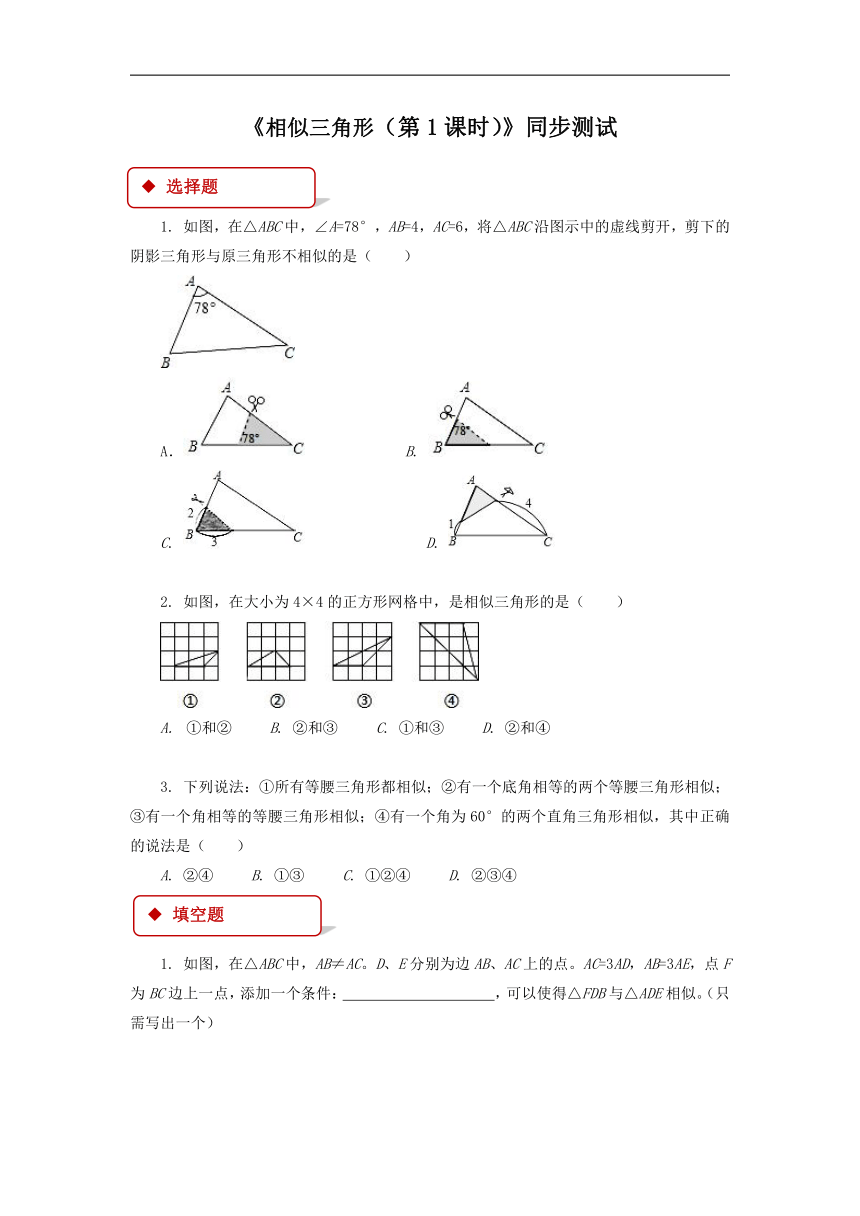 | |
| 格式 | doc | ||
| 文件大小 | 111.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-22 16:41:09 | ||
图片预览


文档简介
《相似三角形(第1课时)》同步测试
1. 如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
B.
C. D.
2. 如图,在大小为4×4的正方形网格中,是相似三角形的是( )
①和② B. ②和③ C. ①和③ D. ②和④
3. 下列说法:①所有等腰三角形都相似;②有一个底角相等的两个等腰三角形相似;③有一个角相等的等腰三角形相似;④有一个角为60°的两个直角三角形相似,其中正确的说法是( )
A. ②④ B. ①③ C. ①②④ D. ②③④
1. 如图,在△ABC中,AB≠AC。D、E分别为边AB、AC上的点。AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件: ,可以使得△FDB与△ADE相似。(只需写出一个)
2. 如图,在△ABC中,∠C=90°,BC=16cm,AC=12cm,点P从点B出发,沿BC以2cm/s的速度向点C移动,点Q从点C出发,以1cm/s的速度向点A移动,若点P、Q分别从点B、C同时出发,设运动时间为t s,当t= 时,△CPQ与△CBA相似。
3. 如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4,以下判断:
①PA+PB+PC+PD的最小值为10;
②若△PAB≌△PDC,则△PAD≌△PBC;
③若S1=S2,则S3=S4;
④若△PAB∽△PDA,则PA=2.4
其中正确的是 。
1. 如图,已知:∠BAC=∠EAD,AB=20.4,AC=48,AE=17,AD=40。
求证:△ABC∽△AED。
2. 如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF。
①求证:△DAE≌△DCF;
②求证:△ABG∽△CFG。
答案与解析
1. C
2. C
3. A
1. DF∥AC,或∠BFD=∠A。
2. 4.8或
3. ①②③④
1. 证明:∵AB=20.4,AC=48,AE=17,AD=40。
∴,,∴,∵∠BAC=∠EAD,
∴△ABC∽△AED。
2. 证明:①∵正方形ABCD,等腰直角三角形EDF,∴∠ADC=∠EDF=90°,AD=CD,DE=DF,∴∠ADE+∠ADF=∠ADF+∠CDF,∴∠ADE=∠CDF,在△ADE和△CDF中,
,∴△ADE≌△CDF;
②延长BA到M,交ED于点M,∵△ADE≌△CDF,
∴∠EAD=∠FCD,即∠EAM+∠MAD=∠BCD+∠BCF,
∵∠MAD=∠BCD=90°,∴∠EAM=∠BCF,
∵∠EAM=∠BAG,∴∠BAG=∠BCF,∵∠AGB=∠CGF,∴△ABG∽△CFG。
选择题
填空题
解答题
选择题
填空题
简答题
1. 如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
B.
C. D.
2. 如图,在大小为4×4的正方形网格中,是相似三角形的是( )
①和② B. ②和③ C. ①和③ D. ②和④
3. 下列说法:①所有等腰三角形都相似;②有一个底角相等的两个等腰三角形相似;③有一个角相等的等腰三角形相似;④有一个角为60°的两个直角三角形相似,其中正确的说法是( )
A. ②④ B. ①③ C. ①②④ D. ②③④
1. 如图,在△ABC中,AB≠AC。D、E分别为边AB、AC上的点。AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件: ,可以使得△FDB与△ADE相似。(只需写出一个)
2. 如图,在△ABC中,∠C=90°,BC=16cm,AC=12cm,点P从点B出发,沿BC以2cm/s的速度向点C移动,点Q从点C出发,以1cm/s的速度向点A移动,若点P、Q分别从点B、C同时出发,设运动时间为t s,当t= 时,△CPQ与△CBA相似。
3. 如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4,以下判断:
①PA+PB+PC+PD的最小值为10;
②若△PAB≌△PDC,则△PAD≌△PBC;
③若S1=S2,则S3=S4;
④若△PAB∽△PDA,则PA=2.4
其中正确的是 。
1. 如图,已知:∠BAC=∠EAD,AB=20.4,AC=48,AE=17,AD=40。
求证:△ABC∽△AED。
2. 如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF。
①求证:△DAE≌△DCF;
②求证:△ABG∽△CFG。
答案与解析
1. C
2. C
3. A
1. DF∥AC,或∠BFD=∠A。
2. 4.8或
3. ①②③④
1. 证明:∵AB=20.4,AC=48,AE=17,AD=40。
∴,,∴,∵∠BAC=∠EAD,
∴△ABC∽△AED。
2. 证明:①∵正方形ABCD,等腰直角三角形EDF,∴∠ADC=∠EDF=90°,AD=CD,DE=DF,∴∠ADE+∠ADF=∠ADF+∠CDF,∴∠ADE=∠CDF,在△ADE和△CDF中,
,∴△ADE≌△CDF;
②延长BA到M,交ED于点M,∵△ADE≌△CDF,
∴∠EAD=∠FCD,即∠EAM+∠MAD=∠BCD+∠BCF,
∵∠MAD=∠BCD=90°,∴∠EAM=∠BCF,
∵∠EAM=∠BAG,∴∠BAG=∠BCF,∵∠AGB=∠CGF,∴△ABG∽△CFG。
选择题
填空题
解答题
选择题
填空题
简答题
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
