人教A版2019选择性必修第一册第一章 空间向量与立体几何 单元测试基础卷(含解析)
文档属性
| 名称 | 人教A版2019选择性必修第一册第一章 空间向量与立体几何 单元测试基础卷(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-22 00:00:00 | ||
图片预览


文档简介
人教A版2019选择性必修第一册
第一章空间向量与立体几何单元测试基础卷(原卷版)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.空间直角坐标系中,点关于轴对称的点的坐标是( )
A. B.
C. D.
2.如图所示,在一个长、宽、高分别为2、3、4的密封的长方体装置中放一个单位正方体礼盒,现以点D为坐标原点,、、分别为x、y、z轴建立空间直角坐标系,则正确的是( )
A.的坐标为 B.的坐标为
C.的长为 D.的长为
3.空间直角坐标系中,已知点,则线段的中点坐标为( )
A. B. C. D.
4.已知空间中三点,,,则( )
A.与是共线向量
B.的单位向量是
C.与夹角的余弦值是
D.平面的一个法向量是
5.两平行平面 , 分别经过坐标原点 和点 ,且两平面的一个法向量 ,则两平面间的距离是
A. B. C. D.
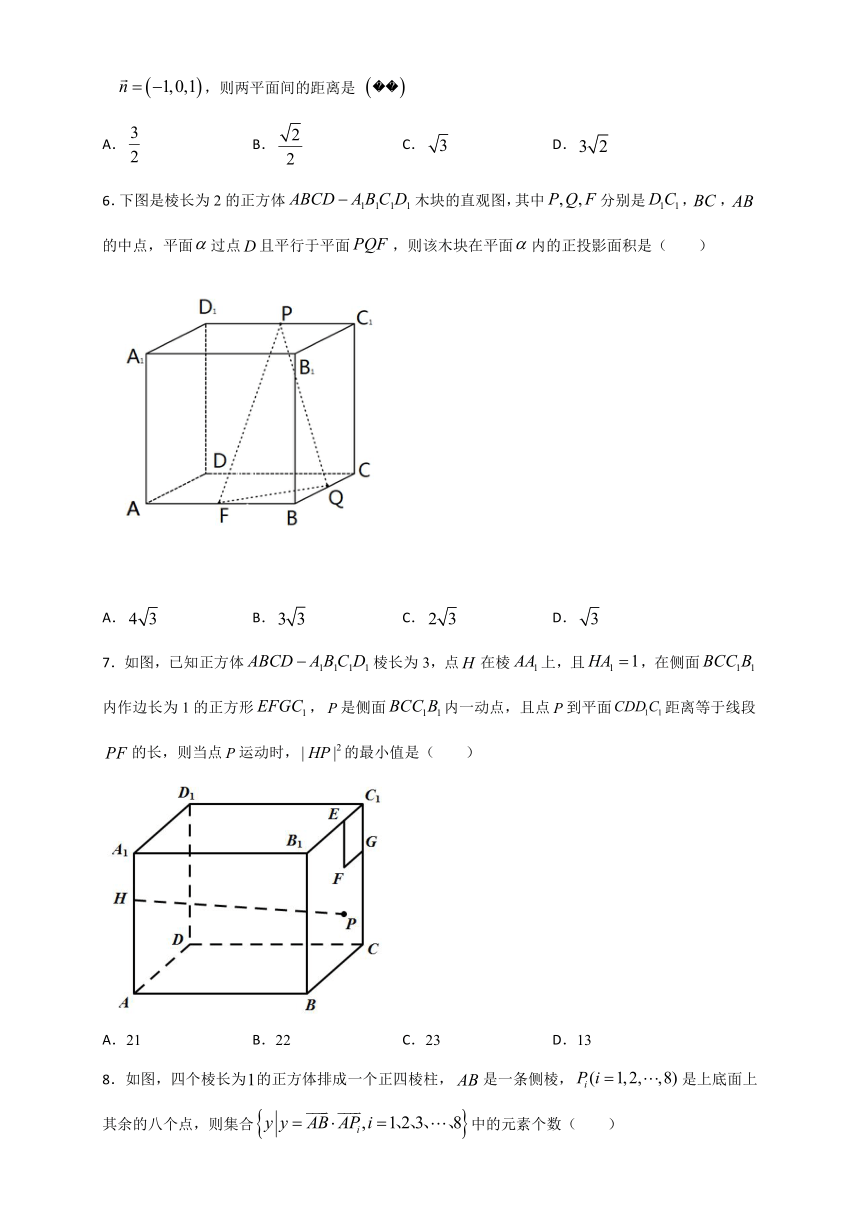
6.下图是棱长为2的正方体木块的直观图,其中分别是,,的中点,平面过点且平行于平面,则该木块在平面内的正投影面积是( )
A. B. C. D.
7.如图,已知正方体棱长为3,点在棱上,且,在侧面内作边长为1的正方形,是侧面内一动点,且点到平面距离等于线段的长,则当点运动时,的最小值是( )
A.21 B.22 C.23 D.13
8.如图,四个棱长为的正方体排成一个正四棱柱,是一条侧棱,是上底面上其余的八个点,则集合中的元素个数( )
A.1 B.2 C.4 D.8
二、多选题
9.给出下列命题,其中正确的有( )
A.空间任意三个向量都可以作为一组基底
B.已知向量,则、与任何向量都不能构成空间的一组基底
C.,,,是空间四点,若,,不能构成空间的一组基底,则,,,共面
D.已知是空间向量的一组基底,若,则也是空间一组基底
10.已知为直线l的方向向量,,分别为平面α,β的法向量(α,β不重合),那么下列选项中,正确的是( )
A.∥ α∥β B.⊥ α⊥β
C.∥ l∥α D.⊥ l∥α
11.在长方体中,,,,以为原点,以分别为轴, 轴,轴正方向建立空间直角坐标系,则下列说法正确的是( )
A.
B.异面直线与所成角的余弦值为
C.平面的一个法向量为
D.二面角的余弦值为
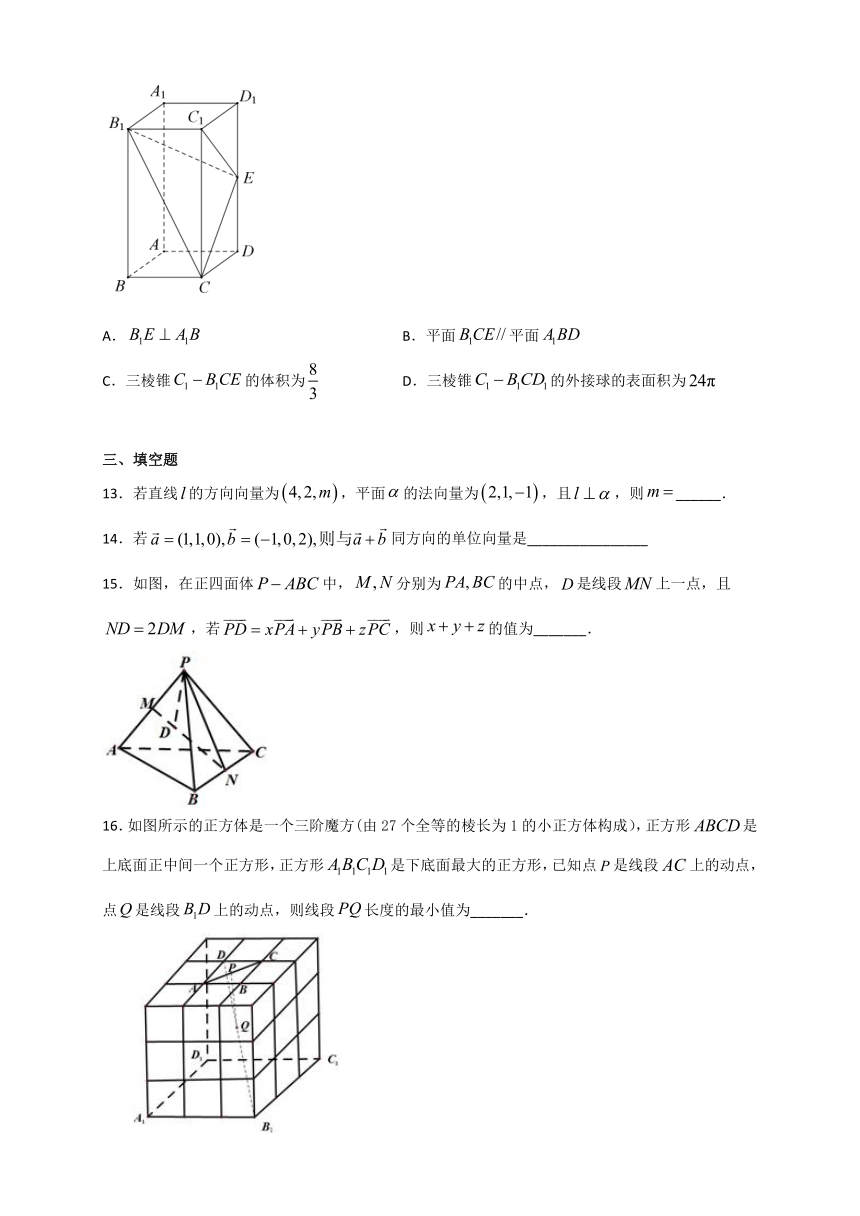
12.若长方体的底面是边长为2的正方形,高为4,是的中点,则( )
A. B.平面平面
C.三棱锥的体积为 D.三棱锥的外接球的表面积为
三、填空题
13.若直线的方向向量为,平面的法向量为,且,则______.
14.若同方向的单位向量是________________
15.如图,在正四面体中,分别为的中点,是线段上一点,且,若,则的值为_______.
16.如图所示的正方体是一个三阶魔方(由27个全等的棱长为1的小正方体构成),正方形是上底面正中间一个正方形,正方形是下底面最大的正方形,已知点是线段上的动点,点是线段上的动点,则线段长度的最小值为_______.
四、解答题
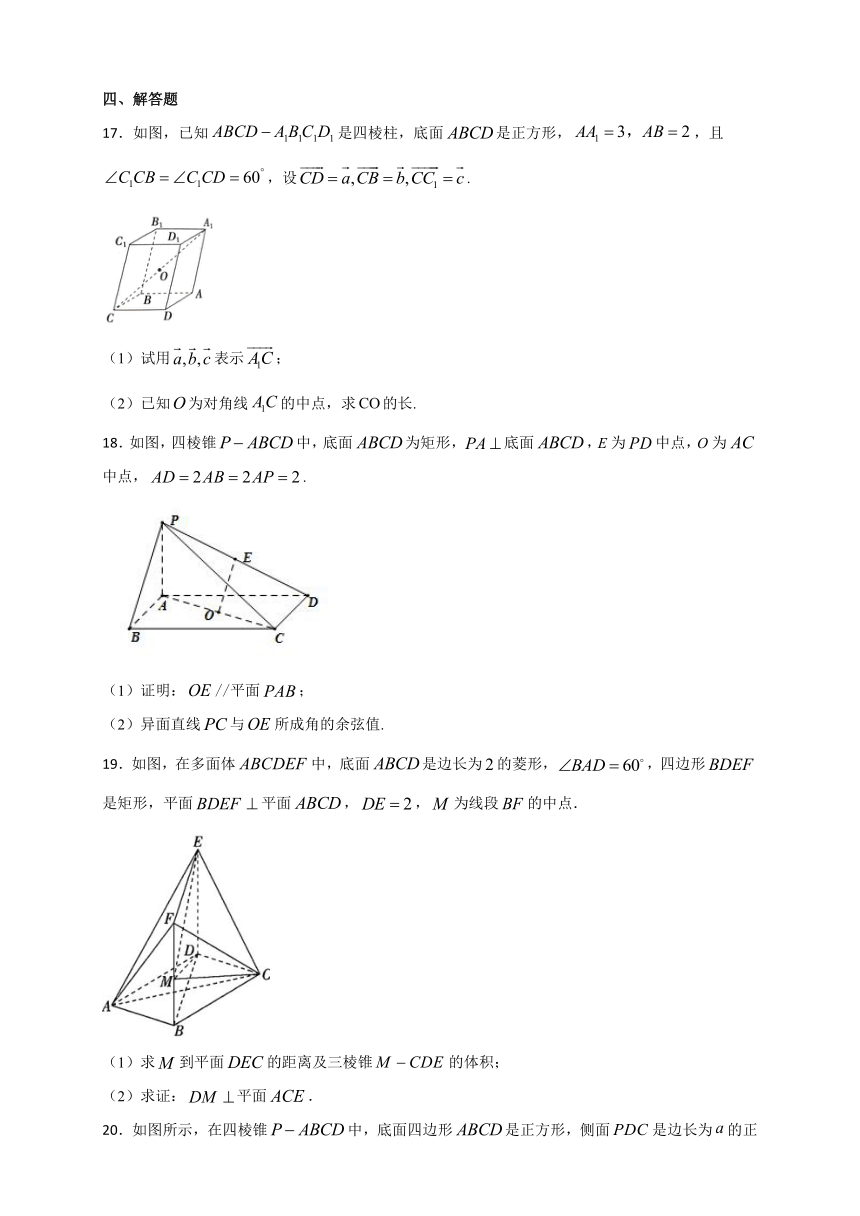
17.如图,已知是四棱柱,底面是正方形,,且,设.
(1)试用表示;
(2)已知为对角线的中点,求的长.
18.如图,四棱锥中,底面为矩形,底面,E为中点,O为中点,.
(1)证明://平面;
(2)异面直线与所成角的余弦值.
19.如图,在多面体中,底面是边长为的菱形,,四边形是矩形,平面平面,,为线段的中点.
(1)求到平面的距离及三棱锥的体积;
(2)求证:平面.
20.如图所示,在四棱锥中,底面四边形是正方形,侧面是边长为的正三角形,且平面底面,为的中点.
(1)求异面直线与所成角的余弦值;
(2)求直线与平面所成角的正弦值.
21.如图,四棱锥中,平面、底面为菱形,为的中点.
(1)证明:平面;
(2)设,菱形的面积为,求二面角的余弦值.
22.如图,在四棱锥中,,,,,平面平面.
(1)求证:平面;
(2)求证:平面;
(3)在棱上是否存在一点E,使得二面角的大小为?若存在,求出的值;若不存在,请说明理由.
人教A版2019选择性必修第一册
第一章空间向量与立体几何单元测试基础卷(解析版)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.空间直角坐标系中,点关于轴对称的点的坐标是( )
A. B.
C. D.
【答案】A
【解析】
【分析】
关于轴对称,纵坐标不变,横坐标、竖坐标变为相反数.
【详解】
关于轴对称的两点的纵坐标相同,横坐标、竖坐标均互为相反数.
所以点关于轴对称的点的坐标是.
故选:A.
【点睛】
本题考查空间平面直角坐标系,考查关于坐标轴、坐标平面对称的问题.属于基础题.
2.如图所示,在一个长、宽、高分别为2、3、4的密封的长方体装置中放一个单位正方体礼盒,现以点D为坐标原点,、、分别为x、y、z轴建立空间直角坐标系,则正确的是( )
A.的坐标为 B.的坐标为
C.的长为 D.的长为
【答案】D
【分析】
根据坐标系写出各点的坐标分析即可.
【详解】
由所建坐标系可得:,,,
.
故选:D.
【点睛】
本题考查空间直角坐标系的应用,考查空间中距离的求法,考查计算能力,属于基础题.
3.空间直角坐标系中,已知点,则线段的中点坐标为( )
A. B. C. D.
【答案】A
【解析】
点,
由中点坐标公式得中得为:,即.
故选A.
4.已知空间中三点,,,则( )
A.与是共线向量
B.的单位向量是
C.与夹角的余弦值是
D.平面的一个法向量是
【答案】D
【分析】
根据向量的相关性质判断.
【详解】
对于A项,,,所以,则与不是共线向量,所以A项错误;
对于B项,因为,所以的单位向量为,所以B项错误;
对于C项,向量,,所以,所以C项错误;
对于D项,设平面的法向量是,因为,,所以,则,令,则平面的一个法向量为,所以D项正确.
故选:D.
【点睛】
本题考查共线向量的判断,单位向量的求法,夹角的求法,平面法向量的求法,属于空间向量综合题.
5.两平行平面 , 分别经过坐标原点 和点 ,且两平面的一个法向量 ,则两平面间的距离是
A. B. C. D.
【答案】B
【解析】
两平行平面 , 分别经过坐标原点 和点 ,,且两平面的一个法向量两平面间的距离,故选B.
6.下图是棱长为2的正方体木块的直观图,其中分别是,,的中点,平面过点且平行于平面,则该木块在平面内的正投影面积是( )
A. B. C. D.
【答案】A
【分析】
先根据题意平面可以平移至平面,即木块在平面内的正投影即可看成是在平面的正投影,根据投影的性质可得投影为正六边形,最后根据正六边形面积公式可求出投影的面积.
【详解】
解:根据题意可知平面过点且平行于平面PQF,
则平面可以平移至平面,
木块在平面内的正投影即可看成是在平面的正投影,
根据投影的性质可得投影为正六边形如图所示,
因为正方体棱长为2,
所以,
则投影面内正六边形的边长为:
根据正六边形面积公式可得投影的面积为:
故投影面积为:
故选:A
【点睛】
本题主要考查空间几何体和正投影得概念,考查面积公式是计算,考查空间想象力和推导能力,属于难题.
7.如图,已知正方体棱长为3,点在棱上,且,在侧面内作边长为1的正方形,是侧面内一动点,且点到平面距离等于线段的长,则当点运动时,的最小值是( )
A.21 B.22 C.23 D.13
【答案】D
【分析】
建立空间直角坐标系,根据在内可设出点坐标,作,连接,可得,作,根据空间中两点间距离公式,再根据二次函数的性质,即可求得的范围.
【详解】
根据题意,以D为原点建立空间直角坐标系如图所示:
作交于M,连接,则
作交于N,则即为点P到平面距离.
设,则
∵点到平面距离等于线段的长
∴
由两点间距离公式可得,化简得,则解不等式可得
综上可得
则在中
所以(当时 取等)
故选:D
【点睛】
本题考查了空间直角坐标系的综合应用,利用空间两点间距离公式及二次函数求最值,属于难题.
8.如图,四个棱长为的正方体排成一个正四棱柱,是一条侧棱,是上底面上其余的八个点,则集合中的元素个数( )
A.1 B.2 C.4 D.8
【答案】A
【分析】
本题首先可根据图像得出,然后将转化为,最后根据棱长为以及即可得出结果.
【详解】
由图像可知,,
则,
因为棱长为,,
所以,,
故集合中的元素个数为,
故选:A.
【点睛】
本题考查向量数量积的求解问题,关键是能够利用平面向量线性运算将所求向量数量积转化为已知模长的向量和有垂直关系向量的数量积的运算问题,考查了转化与化归的思想,考查集合中元素的性质,是中档题.
二、多选题
9.给出下列命题,其中正确的有( )
A.空间任意三个向量都可以作为一组基底
B.已知向量,则、与任何向量都不能构成空间的一组基底
C.,,,是空间四点,若,,不能构成空间的一组基底,则,,,共面
D.已知是空间向量的一组基底,若,则也是空间一组基底
【答案】BCD
【分析】
选项A、B中,根据空间基底的概念,可判断;选项C中,可得共面,又由过相同点B,可得四点共面,由此可判断;选项D中:基向量与向量一定不共面,由此可判断.
【详解】
选项A中,根据空间基底的概念,可得任意三个不共面的向量都可以作为一个空间基底,所以A不正确;
选项B中,根据空间基底的概念,可得B正确;
选项C中,由不能构成空间的一个基底,可得共面,又由过相同点B,可得四点共面,所以C正确;
选项D中:由是空间的一个基底,则基向量与向量一定不共面,所以可以构成空间另一个基底,所以D正确.
故选:BCD.
10.已知为直线l的方向向量,,分别为平面α,β的法向量(α,β不重合),那么下列选项中,正确的是( )
A.∥ α∥β B.⊥ α⊥β
C.∥ l∥α D.⊥ l∥α
【答案】AB
【分析】
根据线面直线的位置关系逐一判断即可.
【详解】
解:为直线l的方向向量,,分别为平面α,β的法向量(α,β不重合),
则∥ α∥β,⊥ α⊥β,∥ l⊥α,⊥ l∥α或l α.
因此AB正确.
故选:AB.
11.在长方体中,,,,以为原点,以分别为轴, 轴,轴正方向建立空间直角坐标系,则下列说法正确的是( )
A.
B.异面直线与所成角的余弦值为
C.平面的一个法向量为
D.二面角的余弦值为
【答案】ACD
【分析】
由向量法对每一选项进行逐一计算验证,可得答案.
【详解】
由题意可得,
选项A: 所以,则A 正确.
选项B:,,所以
所以异面直线与所成角的余弦值为,则B不正确.
选项C:设平面的一个法向量为
由,,则
所以 ,取,得,则C正确.
选项D:由上可得平面的一个法向量为
又平面的法向量为
则
所以二面角的余弦值为,则D正确.
故选:ACD
12.若长方体的底面是边长为2的正方形,高为4,是的中点,则( )
A. B.平面平面
C.三棱锥的体积为 D.三棱锥的外接球的表面积为
【答案】CD
【分析】
以为正交基底建立空间直角坐标系,写出各点坐标,计算值即可判断A;分别求出平面,平面的法向量,判断它们的法向量是否共线,即可判断B;利用等体积法,求出三棱锥的体积即可判断C;三棱锥的外接球即为长方体的外接球,故求出长方体的外接球的表面积即可判断D.
【详解】
以为正交基底建立如图所示的空间直角坐标系,则
,,,,,,,
所以,,
因为,所以与不垂直,故A错误;
,
设平面的一个法向量为,则
由,得,所以,
不妨取,则,
所以,
同理可得设平面的一个法向量为,
故不存在实数使得,故平面与平面不平行,故B错误;
在长方体中,平面,
故是三棱锥的高,
所以,
故C正确;
三棱锥的外接球即为长方体的外接球,
故外接球的半径,
所以三棱锥的外接球的表面积,故D正确.
故选:CD.
【点睛】
本题主要考查用向量法判断线线垂直、面面平行,等体积法的应用及几何体外接球的表面积.
三、填空题
13.若直线的方向向量为,平面的法向量为,且,则______.
【答案】
【分析】
由已知可知,直线的方向向量与平面的法向量平行,根据空间向量平行的充要条件可得到一个关于和的方程组,解方程组即可得到答案.
【详解】
解:,直线的方向向量为,平面的法向量为,
直线的方向向量与平面的法向量平行.
则存在实数使,
即,.
故答案为:.
【点睛】
本题考查向量语言表述线面垂直,直线的方向向量与平面的法向量平行是解本题的关键,属于基础题.
14.若同方向的单位向量是________________
【答案】
【解析】
试题分析:,与同方向的单位向量是
考点:空间向量的坐标运算;
15.如图,在正四面体中,分别为的中点,是线段上一点,且,若,则的值为_______.
【答案】
【分析】
利用基向量表示,结合空间向量基本定理可得.
【详解】
所以,所以.
【点睛】
本题主要考查空间向量的基本定理,把目标向量向基底向量靠拢是求解的主要思路.
16.如图所示的正方体是一个三阶魔方(由27个全等的棱长为1的小正方体构成),正方形是上底面正中间一个正方形,正方形是下底面最大的正方形,已知点是线段上的动点,点是线段上的动点,则线段长度的最小值为_______.
【答案】
【分析】
建立空间直角坐标系,写出点的坐标,求出目标的表达式,从而可得最小值.
【详解】
以为坐标原点,所在直线分别为x轴,y轴建立空间直角坐标系,
则 ,
设,,.
,.
,
当且时,取到最小值,所以线段长度的最小值为.
【点睛】
本题主要考查空间向量的应用,利用空间向量求解距离的最值问题时,一般是把目标式表示出来,结合目标式的特征,选择合适的方法求解最值.
四、解答题
17.如图,已知是四棱柱,底面是正方形,,且,设.
(1)试用表示;
(2)已知为对角线的中点,求的长.
【答案】(1);(2).
【分析】
(1)由可表示出来;
(2)由可计算出.
【详解】
(1)
;
(2)由题意知,
,
,
,
.
【点睛】
本题考查空间向量的线性运算,考查利用向量计算长度,属于基础题.
18.如图,四棱锥中,底面为矩形,底面,E为中点,O为中点,.
(1)证明://平面;
(2)异面直线与所成角的余弦值.
【答案】(1)见详解; (2)
【分析】
(1)连接,得到O为中点,然后利用中位线定理,可得,根据线面平行的判定定理,可得结果.
(2)通过建系,可得,然后利用向量的夹角公式,可得结果.
【详解】
(1)证明:连接,则O为中点,
又E为中点,∴//.
∵平面,平面,
∴//平面
(2)以A为原点建立空间直角坐标系,
如图,
则,
∴,
∴
即异面直线与所成角的余弦值为
【点睛】
本题考查线面平行的判定定理以及建系通过利用向量的方法解决线线角,将几何问题用代数方法来解决,化繁为简,属基础题.
19.如图,在多面体中,底面是边长为的菱形,,四边形是矩形,平面平面,,为线段的中点.
(1)求到平面的距离及三棱锥的体积;
(2)求证:平面.
【答案】(1)到平面的距离为,;(2)证明见解析.
【分析】
(1)设,以为原点,所在直线为轴,所在直线为轴,过且与平面垂直的直线为轴,建立空间直角坐标系,利用空间向量法可求得点到平面的距离,计算出的面积,利用锥体的体积公式可计算出三棱锥的体积;
(2)利用向量法证明出,,可得出,,再利用线面垂直的判定定理可证得平面.
【详解】
(1)设,以为原点,所在直线为轴,所在直线为轴,过且与平面垂直的直线为轴,建立空间直角坐标系,如图所示.
易知轴在平面内,且轴,则、、、,
,,,
设平面的一个法向量,
则,取,得,
到平面的距离,
又,
因此,三棱锥的体积;
(2)证明:由(1)易知,则,,
,,
,,,平面.
【点睛】
本题考查利用空间向量法计算点到平面的距离、三棱锥体积的计算,同时也考查了利用空间向量法证明线面垂直,考查推理能力与计算能力,属于中等题.
20.如图所示,在四棱锥中,底面四边形是正方形,侧面是边长为的正三角形,且平面底面,为的中点.
(1)求异面直线与所成角的余弦值;
(2)求直线与平面所成角的正弦值.
【答案】(1);(2).
【分析】
取的中点,连接,证明出平面,然后以点为坐标原点,、所在的直线分别为、轴建立空间直角坐标系.
(1)写出、的坐标,利用空间向量法可求得异面直线与所成角的余弦值;
(2)求得平面的一个法向量,并写出,利用空间向量法可求得直线与平面所成角的正弦值.
【详解】
取的中点,连接,
为正三角形,为的中点,则.
又平面平面,平面平面,平面,
平面.
以点为坐标原点,、所在的直线分别为、轴建立如下图所示的空间直角坐标系,
则、、、.
(1)设异面直线与所成的角为,
为的中点,,,,
,,,
,
因此,异面直线与所成角的余弦值为;
(2)设直线与平面所成的角为,易知平面的一个法向量为,
.
因此,直线与平面所成角的正弦值为.
【点睛】
本题考查利用空间向量法计算异面直线所成角的余弦值以及线面角的正弦值,考查计算能力,属于中等题.
21.如图,四棱锥中,平面、底面为菱形,为的中点.
(1)证明:平面;
(2)设,菱形的面积为,求二面角的余弦值.
【答案】(1)证明见解析;(2).
【分析】
(1)连接交于点,连接,则,利用线面平行的判定定理,即可得证;
(2)根据题意,求得菱形的边长,取中点,可证,如图建系,求得点坐标及坐标,即可求得平面的法向量,根据平面PAD,可求得面的法向量,利用空间向量的夹角公式,即可求得答案.
【详解】
(1)连接交于点,连接,
则、E分别为、的中点,所以,
又平面平面
所以平面
(2)由菱形的面积为,,易得菱形边长为,
取中点,连接,因为,所以,
以点为原点,以方向为轴,方向为轴,方向为轴,建立如图所示坐标系.
则
所以
设平面的法向量,由
得,令,则
所以一个法向量,
因为,,所以平面PAD,
所以平面的一个法向量
所以,
又二面角为锐二面角,所以二面角的余弦值为
【点睛】
解题的关键是熟练掌握证明平行的定理,证明线面平行时,常用中位线法和平行四边形法来证明;利用空间向量求解二面角为常考题型,步骤为建系、求点坐标、求所需向量坐标、求法向量、利用夹角公式求解,属基础题.
22.如图,在四棱锥中,,,,,平面平面.
(1)求证:平面;
(2)求证:平面;
(3)在棱上是否存在一点E,使得二面角的大小为?若存在,求出的值;若不存在,请说明理由.
【答案】(1)证明见解析(2)证明见解析(3)存在;
【分析】
(1)由线面平行判定定理证明即可;
(2)由勾股定理得出,进而得,再由面面垂直的性质定理即可证明平面;
(3)建立空间直角坐标系,利用向量法求解即可.
【详解】
证明:(1)因为,
平面,
平面,
所以平面.
(2)取的中点N,连接.
在直角梯形中,
易知,且.
在中,由勾股定理得.
在中,由勾股定理逆定理可知.
又因为平面平面,
且平面平面,
所以平面.
(3)取的中点O,连接,.
所以,
因为平面,
所以平面.
因为,
所以.
如图建立空间直角坐标系,
则,,,,
,,.
易知平面的一个法向量为.
假设在棱上存在一点E,使得二面角的大小为.
不妨设(),
所以,
设为平面的一个法向量,
则 即
令,,所以.
从而.
解得或.
因为,所以.
由题知二面角为锐二面角.
所以在棱上存在一点E,使得二面角的大小为,
此时.
【点睛】
本题主要考查了证明线面平行,线面垂直以及由面面角求其他量,属于中档题.
第一章空间向量与立体几何单元测试基础卷(原卷版)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.空间直角坐标系中,点关于轴对称的点的坐标是( )
A. B.
C. D.
2.如图所示,在一个长、宽、高分别为2、3、4的密封的长方体装置中放一个单位正方体礼盒,现以点D为坐标原点,、、分别为x、y、z轴建立空间直角坐标系,则正确的是( )
A.的坐标为 B.的坐标为
C.的长为 D.的长为
3.空间直角坐标系中,已知点,则线段的中点坐标为( )
A. B. C. D.
4.已知空间中三点,,,则( )
A.与是共线向量
B.的单位向量是
C.与夹角的余弦值是
D.平面的一个法向量是
5.两平行平面 , 分别经过坐标原点 和点 ,且两平面的一个法向量 ,则两平面间的距离是
A. B. C. D.
6.下图是棱长为2的正方体木块的直观图,其中分别是,,的中点,平面过点且平行于平面,则该木块在平面内的正投影面积是( )
A. B. C. D.
7.如图,已知正方体棱长为3,点在棱上,且,在侧面内作边长为1的正方形,是侧面内一动点,且点到平面距离等于线段的长,则当点运动时,的最小值是( )
A.21 B.22 C.23 D.13
8.如图,四个棱长为的正方体排成一个正四棱柱,是一条侧棱,是上底面上其余的八个点,则集合中的元素个数( )
A.1 B.2 C.4 D.8
二、多选题
9.给出下列命题,其中正确的有( )
A.空间任意三个向量都可以作为一组基底
B.已知向量,则、与任何向量都不能构成空间的一组基底
C.,,,是空间四点,若,,不能构成空间的一组基底,则,,,共面
D.已知是空间向量的一组基底,若,则也是空间一组基底
10.已知为直线l的方向向量,,分别为平面α,β的法向量(α,β不重合),那么下列选项中,正确的是( )
A.∥ α∥β B.⊥ α⊥β
C.∥ l∥α D.⊥ l∥α
11.在长方体中,,,,以为原点,以分别为轴, 轴,轴正方向建立空间直角坐标系,则下列说法正确的是( )
A.
B.异面直线与所成角的余弦值为
C.平面的一个法向量为
D.二面角的余弦值为
12.若长方体的底面是边长为2的正方形,高为4,是的中点,则( )
A. B.平面平面
C.三棱锥的体积为 D.三棱锥的外接球的表面积为
三、填空题
13.若直线的方向向量为,平面的法向量为,且,则______.
14.若同方向的单位向量是________________
15.如图,在正四面体中,分别为的中点,是线段上一点,且,若,则的值为_______.
16.如图所示的正方体是一个三阶魔方(由27个全等的棱长为1的小正方体构成),正方形是上底面正中间一个正方形,正方形是下底面最大的正方形,已知点是线段上的动点,点是线段上的动点,则线段长度的最小值为_______.
四、解答题
17.如图,已知是四棱柱,底面是正方形,,且,设.
(1)试用表示;
(2)已知为对角线的中点,求的长.
18.如图,四棱锥中,底面为矩形,底面,E为中点,O为中点,.
(1)证明://平面;
(2)异面直线与所成角的余弦值.
19.如图,在多面体中,底面是边长为的菱形,,四边形是矩形,平面平面,,为线段的中点.
(1)求到平面的距离及三棱锥的体积;
(2)求证:平面.
20.如图所示,在四棱锥中,底面四边形是正方形,侧面是边长为的正三角形,且平面底面,为的中点.
(1)求异面直线与所成角的余弦值;
(2)求直线与平面所成角的正弦值.
21.如图,四棱锥中,平面、底面为菱形,为的中点.
(1)证明:平面;
(2)设,菱形的面积为,求二面角的余弦值.
22.如图,在四棱锥中,,,,,平面平面.
(1)求证:平面;
(2)求证:平面;
(3)在棱上是否存在一点E,使得二面角的大小为?若存在,求出的值;若不存在,请说明理由.
人教A版2019选择性必修第一册
第一章空间向量与立体几何单元测试基础卷(解析版)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.空间直角坐标系中,点关于轴对称的点的坐标是( )
A. B.
C. D.
【答案】A
【解析】
【分析】
关于轴对称,纵坐标不变,横坐标、竖坐标变为相反数.
【详解】
关于轴对称的两点的纵坐标相同,横坐标、竖坐标均互为相反数.
所以点关于轴对称的点的坐标是.
故选:A.
【点睛】
本题考查空间平面直角坐标系,考查关于坐标轴、坐标平面对称的问题.属于基础题.
2.如图所示,在一个长、宽、高分别为2、3、4的密封的长方体装置中放一个单位正方体礼盒,现以点D为坐标原点,、、分别为x、y、z轴建立空间直角坐标系,则正确的是( )
A.的坐标为 B.的坐标为
C.的长为 D.的长为
【答案】D
【分析】
根据坐标系写出各点的坐标分析即可.
【详解】
由所建坐标系可得:,,,
.
故选:D.
【点睛】
本题考查空间直角坐标系的应用,考查空间中距离的求法,考查计算能力,属于基础题.
3.空间直角坐标系中,已知点,则线段的中点坐标为( )
A. B. C. D.
【答案】A
【解析】
点,
由中点坐标公式得中得为:,即.
故选A.
4.已知空间中三点,,,则( )
A.与是共线向量
B.的单位向量是
C.与夹角的余弦值是
D.平面的一个法向量是
【答案】D
【分析】
根据向量的相关性质判断.
【详解】
对于A项,,,所以,则与不是共线向量,所以A项错误;
对于B项,因为,所以的单位向量为,所以B项错误;
对于C项,向量,,所以,所以C项错误;
对于D项,设平面的法向量是,因为,,所以,则,令,则平面的一个法向量为,所以D项正确.
故选:D.
【点睛】
本题考查共线向量的判断,单位向量的求法,夹角的求法,平面法向量的求法,属于空间向量综合题.
5.两平行平面 , 分别经过坐标原点 和点 ,且两平面的一个法向量 ,则两平面间的距离是
A. B. C. D.
【答案】B
【解析】
两平行平面 , 分别经过坐标原点 和点 ,,且两平面的一个法向量两平面间的距离,故选B.
6.下图是棱长为2的正方体木块的直观图,其中分别是,,的中点,平面过点且平行于平面,则该木块在平面内的正投影面积是( )
A. B. C. D.
【答案】A
【分析】
先根据题意平面可以平移至平面,即木块在平面内的正投影即可看成是在平面的正投影,根据投影的性质可得投影为正六边形,最后根据正六边形面积公式可求出投影的面积.
【详解】
解:根据题意可知平面过点且平行于平面PQF,
则平面可以平移至平面,
木块在平面内的正投影即可看成是在平面的正投影,
根据投影的性质可得投影为正六边形如图所示,
因为正方体棱长为2,
所以,
则投影面内正六边形的边长为:
根据正六边形面积公式可得投影的面积为:
故投影面积为:
故选:A
【点睛】
本题主要考查空间几何体和正投影得概念,考查面积公式是计算,考查空间想象力和推导能力,属于难题.
7.如图,已知正方体棱长为3,点在棱上,且,在侧面内作边长为1的正方形,是侧面内一动点,且点到平面距离等于线段的长,则当点运动时,的最小值是( )
A.21 B.22 C.23 D.13
【答案】D
【分析】
建立空间直角坐标系,根据在内可设出点坐标,作,连接,可得,作,根据空间中两点间距离公式,再根据二次函数的性质,即可求得的范围.
【详解】
根据题意,以D为原点建立空间直角坐标系如图所示:
作交于M,连接,则
作交于N,则即为点P到平面距离.
设,则
∵点到平面距离等于线段的长
∴
由两点间距离公式可得,化简得,则解不等式可得
综上可得
则在中
所以(当时 取等)
故选:D
【点睛】
本题考查了空间直角坐标系的综合应用,利用空间两点间距离公式及二次函数求最值,属于难题.
8.如图,四个棱长为的正方体排成一个正四棱柱,是一条侧棱,是上底面上其余的八个点,则集合中的元素个数( )
A.1 B.2 C.4 D.8
【答案】A
【分析】
本题首先可根据图像得出,然后将转化为,最后根据棱长为以及即可得出结果.
【详解】
由图像可知,,
则,
因为棱长为,,
所以,,
故集合中的元素个数为,
故选:A.
【点睛】
本题考查向量数量积的求解问题,关键是能够利用平面向量线性运算将所求向量数量积转化为已知模长的向量和有垂直关系向量的数量积的运算问题,考查了转化与化归的思想,考查集合中元素的性质,是中档题.
二、多选题
9.给出下列命题,其中正确的有( )
A.空间任意三个向量都可以作为一组基底
B.已知向量,则、与任何向量都不能构成空间的一组基底
C.,,,是空间四点,若,,不能构成空间的一组基底,则,,,共面
D.已知是空间向量的一组基底,若,则也是空间一组基底
【答案】BCD
【分析】
选项A、B中,根据空间基底的概念,可判断;选项C中,可得共面,又由过相同点B,可得四点共面,由此可判断;选项D中:基向量与向量一定不共面,由此可判断.
【详解】
选项A中,根据空间基底的概念,可得任意三个不共面的向量都可以作为一个空间基底,所以A不正确;
选项B中,根据空间基底的概念,可得B正确;
选项C中,由不能构成空间的一个基底,可得共面,又由过相同点B,可得四点共面,所以C正确;
选项D中:由是空间的一个基底,则基向量与向量一定不共面,所以可以构成空间另一个基底,所以D正确.
故选:BCD.
10.已知为直线l的方向向量,,分别为平面α,β的法向量(α,β不重合),那么下列选项中,正确的是( )
A.∥ α∥β B.⊥ α⊥β
C.∥ l∥α D.⊥ l∥α
【答案】AB
【分析】
根据线面直线的位置关系逐一判断即可.
【详解】
解:为直线l的方向向量,,分别为平面α,β的法向量(α,β不重合),
则∥ α∥β,⊥ α⊥β,∥ l⊥α,⊥ l∥α或l α.
因此AB正确.
故选:AB.
11.在长方体中,,,,以为原点,以分别为轴, 轴,轴正方向建立空间直角坐标系,则下列说法正确的是( )
A.
B.异面直线与所成角的余弦值为
C.平面的一个法向量为
D.二面角的余弦值为
【答案】ACD
【分析】
由向量法对每一选项进行逐一计算验证,可得答案.
【详解】
由题意可得,
选项A: 所以,则A 正确.
选项B:,,所以
所以异面直线与所成角的余弦值为,则B不正确.
选项C:设平面的一个法向量为
由,,则
所以 ,取,得,则C正确.
选项D:由上可得平面的一个法向量为
又平面的法向量为
则
所以二面角的余弦值为,则D正确.
故选:ACD
12.若长方体的底面是边长为2的正方形,高为4,是的中点,则( )
A. B.平面平面
C.三棱锥的体积为 D.三棱锥的外接球的表面积为
【答案】CD
【分析】
以为正交基底建立空间直角坐标系,写出各点坐标,计算值即可判断A;分别求出平面,平面的法向量,判断它们的法向量是否共线,即可判断B;利用等体积法,求出三棱锥的体积即可判断C;三棱锥的外接球即为长方体的外接球,故求出长方体的外接球的表面积即可判断D.
【详解】
以为正交基底建立如图所示的空间直角坐标系,则
,,,,,,,
所以,,
因为,所以与不垂直,故A错误;
,
设平面的一个法向量为,则
由,得,所以,
不妨取,则,
所以,
同理可得设平面的一个法向量为,
故不存在实数使得,故平面与平面不平行,故B错误;
在长方体中,平面,
故是三棱锥的高,
所以,
故C正确;
三棱锥的外接球即为长方体的外接球,
故外接球的半径,
所以三棱锥的外接球的表面积,故D正确.
故选:CD.
【点睛】
本题主要考查用向量法判断线线垂直、面面平行,等体积法的应用及几何体外接球的表面积.
三、填空题
13.若直线的方向向量为,平面的法向量为,且,则______.
【答案】
【分析】
由已知可知,直线的方向向量与平面的法向量平行,根据空间向量平行的充要条件可得到一个关于和的方程组,解方程组即可得到答案.
【详解】
解:,直线的方向向量为,平面的法向量为,
直线的方向向量与平面的法向量平行.
则存在实数使,
即,.
故答案为:.
【点睛】
本题考查向量语言表述线面垂直,直线的方向向量与平面的法向量平行是解本题的关键,属于基础题.
14.若同方向的单位向量是________________
【答案】
【解析】
试题分析:,与同方向的单位向量是
考点:空间向量的坐标运算;
15.如图,在正四面体中,分别为的中点,是线段上一点,且,若,则的值为_______.
【答案】
【分析】
利用基向量表示,结合空间向量基本定理可得.
【详解】
所以,所以.
【点睛】
本题主要考查空间向量的基本定理,把目标向量向基底向量靠拢是求解的主要思路.
16.如图所示的正方体是一个三阶魔方(由27个全等的棱长为1的小正方体构成),正方形是上底面正中间一个正方形,正方形是下底面最大的正方形,已知点是线段上的动点,点是线段上的动点,则线段长度的最小值为_______.
【答案】
【分析】
建立空间直角坐标系,写出点的坐标,求出目标的表达式,从而可得最小值.
【详解】
以为坐标原点,所在直线分别为x轴,y轴建立空间直角坐标系,
则 ,
设,,.
,.
,
当且时,取到最小值,所以线段长度的最小值为.
【点睛】
本题主要考查空间向量的应用,利用空间向量求解距离的最值问题时,一般是把目标式表示出来,结合目标式的特征,选择合适的方法求解最值.
四、解答题
17.如图,已知是四棱柱,底面是正方形,,且,设.
(1)试用表示;
(2)已知为对角线的中点,求的长.
【答案】(1);(2).
【分析】
(1)由可表示出来;
(2)由可计算出.
【详解】
(1)
;
(2)由题意知,
,
,
,
.
【点睛】
本题考查空间向量的线性运算,考查利用向量计算长度,属于基础题.
18.如图,四棱锥中,底面为矩形,底面,E为中点,O为中点,.
(1)证明://平面;
(2)异面直线与所成角的余弦值.
【答案】(1)见详解; (2)
【分析】
(1)连接,得到O为中点,然后利用中位线定理,可得,根据线面平行的判定定理,可得结果.
(2)通过建系,可得,然后利用向量的夹角公式,可得结果.
【详解】
(1)证明:连接,则O为中点,
又E为中点,∴//.
∵平面,平面,
∴//平面
(2)以A为原点建立空间直角坐标系,
如图,
则,
∴,
∴
即异面直线与所成角的余弦值为
【点睛】
本题考查线面平行的判定定理以及建系通过利用向量的方法解决线线角,将几何问题用代数方法来解决,化繁为简,属基础题.
19.如图,在多面体中,底面是边长为的菱形,,四边形是矩形,平面平面,,为线段的中点.
(1)求到平面的距离及三棱锥的体积;
(2)求证:平面.
【答案】(1)到平面的距离为,;(2)证明见解析.
【分析】
(1)设,以为原点,所在直线为轴,所在直线为轴,过且与平面垂直的直线为轴,建立空间直角坐标系,利用空间向量法可求得点到平面的距离,计算出的面积,利用锥体的体积公式可计算出三棱锥的体积;
(2)利用向量法证明出,,可得出,,再利用线面垂直的判定定理可证得平面.
【详解】
(1)设,以为原点,所在直线为轴,所在直线为轴,过且与平面垂直的直线为轴,建立空间直角坐标系,如图所示.
易知轴在平面内,且轴,则、、、,
,,,
设平面的一个法向量,
则,取,得,
到平面的距离,
又,
因此,三棱锥的体积;
(2)证明:由(1)易知,则,,
,,
,,,平面.
【点睛】
本题考查利用空间向量法计算点到平面的距离、三棱锥体积的计算,同时也考查了利用空间向量法证明线面垂直,考查推理能力与计算能力,属于中等题.
20.如图所示,在四棱锥中,底面四边形是正方形,侧面是边长为的正三角形,且平面底面,为的中点.
(1)求异面直线与所成角的余弦值;
(2)求直线与平面所成角的正弦值.
【答案】(1);(2).
【分析】
取的中点,连接,证明出平面,然后以点为坐标原点,、所在的直线分别为、轴建立空间直角坐标系.
(1)写出、的坐标,利用空间向量法可求得异面直线与所成角的余弦值;
(2)求得平面的一个法向量,并写出,利用空间向量法可求得直线与平面所成角的正弦值.
【详解】
取的中点,连接,
为正三角形,为的中点,则.
又平面平面,平面平面,平面,
平面.
以点为坐标原点,、所在的直线分别为、轴建立如下图所示的空间直角坐标系,
则、、、.
(1)设异面直线与所成的角为,
为的中点,,,,
,,,
,
因此,异面直线与所成角的余弦值为;
(2)设直线与平面所成的角为,易知平面的一个法向量为,
.
因此,直线与平面所成角的正弦值为.
【点睛】
本题考查利用空间向量法计算异面直线所成角的余弦值以及线面角的正弦值,考查计算能力,属于中等题.
21.如图,四棱锥中,平面、底面为菱形,为的中点.
(1)证明:平面;
(2)设,菱形的面积为,求二面角的余弦值.
【答案】(1)证明见解析;(2).
【分析】
(1)连接交于点,连接,则,利用线面平行的判定定理,即可得证;
(2)根据题意,求得菱形的边长,取中点,可证,如图建系,求得点坐标及坐标,即可求得平面的法向量,根据平面PAD,可求得面的法向量,利用空间向量的夹角公式,即可求得答案.
【详解】
(1)连接交于点,连接,
则、E分别为、的中点,所以,
又平面平面
所以平面
(2)由菱形的面积为,,易得菱形边长为,
取中点,连接,因为,所以,
以点为原点,以方向为轴,方向为轴,方向为轴,建立如图所示坐标系.
则
所以
设平面的法向量,由
得,令,则
所以一个法向量,
因为,,所以平面PAD,
所以平面的一个法向量
所以,
又二面角为锐二面角,所以二面角的余弦值为
【点睛】
解题的关键是熟练掌握证明平行的定理,证明线面平行时,常用中位线法和平行四边形法来证明;利用空间向量求解二面角为常考题型,步骤为建系、求点坐标、求所需向量坐标、求法向量、利用夹角公式求解,属基础题.
22.如图,在四棱锥中,,,,,平面平面.
(1)求证:平面;
(2)求证:平面;
(3)在棱上是否存在一点E,使得二面角的大小为?若存在,求出的值;若不存在,请说明理由.
【答案】(1)证明见解析(2)证明见解析(3)存在;
【分析】
(1)由线面平行判定定理证明即可;
(2)由勾股定理得出,进而得,再由面面垂直的性质定理即可证明平面;
(3)建立空间直角坐标系,利用向量法求解即可.
【详解】
证明:(1)因为,
平面,
平面,
所以平面.
(2)取的中点N,连接.
在直角梯形中,
易知,且.
在中,由勾股定理得.
在中,由勾股定理逆定理可知.
又因为平面平面,
且平面平面,
所以平面.
(3)取的中点O,连接,.
所以,
因为平面,
所以平面.
因为,
所以.
如图建立空间直角坐标系,
则,,,,
,,.
易知平面的一个法向量为.
假设在棱上存在一点E,使得二面角的大小为.
不妨设(),
所以,
设为平面的一个法向量,
则 即
令,,所以.
从而.
解得或.
因为,所以.
由题知二面角为锐二面角.
所以在棱上存在一点E,使得二面角的大小为,
此时.
【点睛】
本题主要考查了证明线面平行,线面垂直以及由面面角求其他量,属于中档题.
