2023-2024学年人教版八年级数学上册 13章 轴对称 单元复习课件 44张PPT
文档属性
| 名称 | 2023-2024学年人教版八年级数学上册 13章 轴对称 单元复习课件 44张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 659.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-22 18:40:36 | ||
图片预览







文档简介
(共44张PPT)
第十三章 轴对称
《轴对称》单元复习
知识点一:轴对称及轴对称图形的相关知识
(1)一个图形沿着一条直线折叠,如果直线两旁的部分能够
,那么这个图形就叫做轴对称图形.这条直线叫做 .
(2)把一个图形沿着某一条直线折叠,如果它能与另一个图形完全 ,那么就说这两个图形关于这条直线(成轴)对称.这条直线叫做 .折叠后重合的点是对应点,叫做 .
对称点
对称轴
重合
对称轴
互相重合
(3)如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的 .
(4)在平面直角坐标系中,关于x轴对称的点的横坐标
,纵坐标 ;关于y轴对称的点的横坐标 ,纵坐标 .
(5)方法指引:注意轴对称图形和轴对称的区别与联系.轴对称图形的对称轴,是任何一对对应点所连线段的
.
垂直平分线
相等
互为相反数
互为相反数
相等
垂直平分线
A B C D
1.(跨学科融合、传统文化)(2022北京一模)2022年北京和张家口成功举办了第24届冬奥会和冬残奥会.下面关于奥运会的剪纸图片中是轴对称图形的是( )
D
2.如图,∠A=30°,∠C'=60°,△ABC与△A'B'C'关于直线l对称,则∠B的度数为( )
A.30° B.60°
C.90° D.120°
C
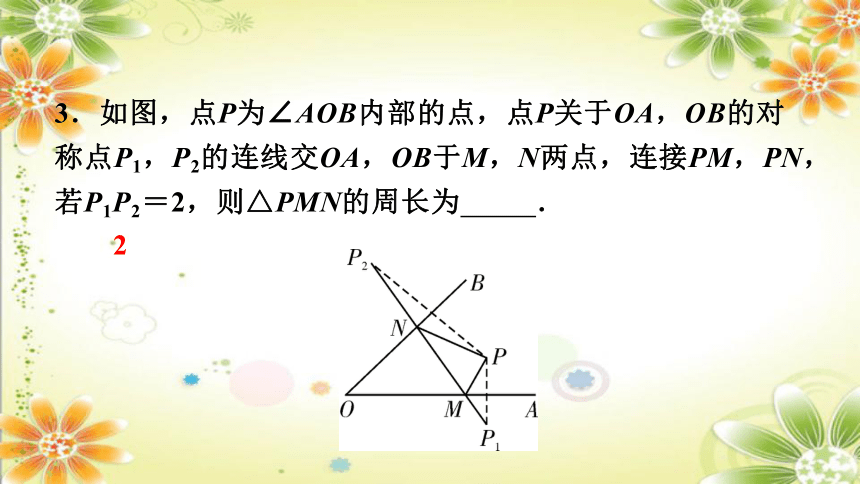
3.如图,点P为∠AOB内部的点,点P关于OA,OB的对称点P1,P2的连线交OA,OB于M,N两点,连接PM,PN,若P1P2=2,则△PMN的周长为 .
2
4.点A(4,1)关于x轴的对称点B的坐标是 .
5.若点A关于y轴对称的点是(2,3),则点A的坐标为
.
(-2,3)
(4,-1)
知识点二:垂直平分线的性质及判定
(1)定义:经过线段的 且与线段 的直线,叫做线段的垂直平分线.
如图1,∵ ,
∴直线m是线段AB的垂直平分线.
(2)性质:线段垂直平分线上的点与线段
两个端点的距离 .
相等
CA=CB,直线m⊥AB于C
垂直
中点
∵CA=CB,直线m⊥AB于C,点P是直线m上的点,
∴ .
如图2,
PA=PB
6.如图,AC⊥BC,DE是AB的垂直平分线,
∠CAE=30°,则∠B= °.
30
7.如图,在△ABC中,BC=4,AB的垂直平分线交AC于点D,若AC=6,则△BCD的周长为 .
10
∵PA=PB,
直线m是线段AB的垂直平分线,
∴ .
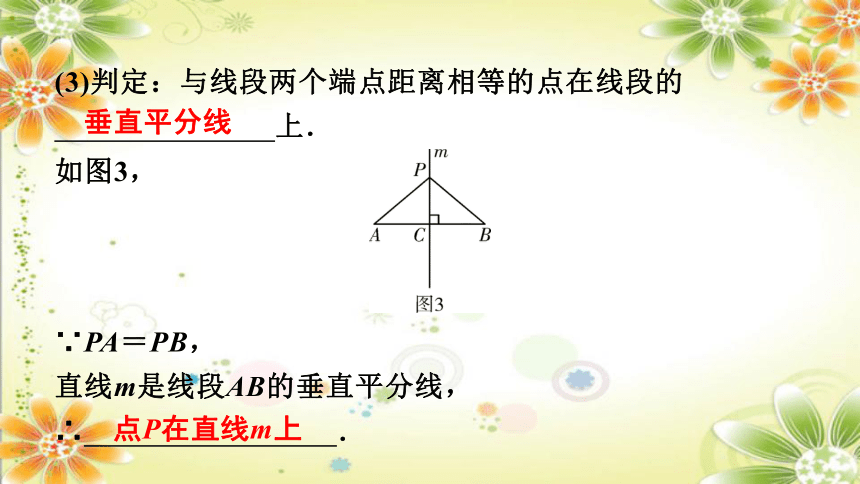
(3)判定:与线段两个端点距离相等的点在线段的
上.
如图3,
点P在直线m上
垂直平分线
8.(全国视野)(2022吉林模拟)如图,在△ABC中,AB的垂直平分线l1交AB于点M,交BC于点D,AC的垂直平分线l2交AC于点N,交BC于点E,l1与l2相交于点O,△ADE的周长为10.
(1)BC的长为 ;
(2)试判断点O是否在边BC的垂直平分线上,并说明理由.
10
解:(2)点O在边BC的垂直平分线上,理由:
连接AO,BO,CO,
∵l1与l2分别是AB,AC的垂直平分线,
∴AO=BO,CO=AO,∴OB=OC,
∴点O在边BC的垂直平分线上.
知识点三:等腰三角形的性质及判定
等腰三角形的性质
(1)等腰三角形的两个底角 .
(简写成“ ”)
(2)等腰三角形的顶角平分线、底边上的 、底边上的 互相重合.(简写成“ ”)
三线合一
高
中线
等边对等角
相等
等腰三角形的判定
(3)定义:有两边 的三角形叫做等腰三角形.
(4)判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也 .(简写成“ ”)
等角对等边
相等
相等
等边三角形的性质
(5)等边三角形是 的特殊的等腰三角形.
(6)等边三角形的三个内角都 ,并且每一个内角都等于 .
60°
相等
三边都相等
等边三角形的判定
(7)由等边三角形的定义判定:三边都 的三角形是等边三角形.
(8)三个角都 的三角形是等边三角形.
(9)有一个角是 的等腰三角形是等边三角形.
60°
相等
相等
含30°角的直角三角形的性质
(10)在直角三角形中,30°角所对的直角边等于
.
斜边的一半
9.如图,在△ABC中,AC=AD=BD,∠B=28°,则∠CAD的度数为 .
68°
10.如图,在△ABC中,∠B=90°,∠BAC=60°,
AB=1,D是BC边延长线上的一点,且∠D=15°,则CD的长为 .
2
11.如图,已知AB∥CD,AC平分∠DAB.求证:△ADC是等腰三角形.
证明:∵AB∥CD,
∴∠BAC=∠DCA,
∵AC平分∠DAB,
∴∠BAC=∠DAC,
∴∠DAC=∠DCA,
∴AD=CD,∴△ADC是等腰三角形.
A B C D
12.【例1】(跨学科融合)(2023鄂州)“国士无双”是人民对“杂交水稻之父”袁隆平院士的赞誉.下列四个汉字中是轴对称图形的是( )
B
小结:利用角平分线、垂直平分线和直角三角形的性质求解.
13.【例2】如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E.若BC=3,则DE的长为( )
A.1 B.2
C.3 D.4
A
小结:关于y轴对称的点的坐标特征是纵坐标相同,横坐标相反.
14.【例3】若点M(a,-3)与点N(1,b)关于y轴对称,则a= ,b= .
-3
-1
小结:求出各个角的度数可得答案.
A.3个
B.4个
C.5个
D.6个
15.【例4】如图,在△ABC中,AB=AC,D,E是BC上两点,∠BAD=∠DAE=∠EAC=36°,则等腰三角形有( )
D
小结:利用等边对等角得到角相等,再利用等角对等边得到答案.
16.【例5】如图,在△ABC中,AB=AC,点E在CA的延长线上,EP⊥BC于点P,交AB于点F,若AF=2,BF=3,则CE的长度为 .
7
小结:充分运用30°角所对直角边等于斜边的一半求解.
A.2 B.4
C.6 D.8
17.【例6】(2022中山一模)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD是斜边AB上的高,
BD=2,则AD的长为( )
C
18.【例7】如图,在△ABC中,AC=4,BC=8,AB的垂直平分线交BC于点D,点E是垂足,求△ACD的周长.
解:∵AB的垂直平分线交BC于点D,∴DA=DB,
∵△ACD的周长=DA+DC+AC,
∴△ACD的周长=DB+DC+AC=BC+AC,
而AC=4,BC=8,∴△ACD的周长=8+4=12.
小结:运用线段垂直平分线的性质定理求解.
19.【例8】(全国视野)(2023淄博)如图,在△ABC中,∠ABC的平分线交AC于点D,过点D作DE∥BC交AB于点E.
(1)求证:BE=DE;
(2)若∠A=80°,∠C=40°,求∠BDE的度数.
(1)证明:∵在△ABC中,∠ABC的平分线交AC于点D,
∴∠ABD=∠CBD,
∵DE∥BC,∴∠EDB=∠CBD,
∴∠EBD=∠EDB,∴BE=DE.
(2)解:∵∠A=80°,∠C=40°,∴∠ABC=60°,
∵∠ABC的平分线交AC于点D,
∴∠ABD=∠CBD=∠ABC=30°,
由(1)知∠EDB=∠EBD,故∠BDE的度数为30°.
小结:角的平分线和平行线结合可得等腰三角形.
A B C D
21.(跨学科融合)(2022金华模拟)自新冠肺炎疫情发生以来,全国人民共同抗疫,某中学积极普及科学防控知识,下面是科学防控知识的图片,其中是轴对称图形的是( )
B
22.(创新题)如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,交AB于点D,若△BCE的周长为8,且AC-BC=2,则AB= .
5
23.已知点A(m-1,3)与点
B(2,n+1)关于x轴对称,则m+n的值为 .
-1
A.①③④ B.①②③④ C.①②④ D.①③
① ② ③ ④
24.如图,在三角形中,AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( )
A
25.(创新题)(2023广州)如图,在△ABC中,AC=BC,∠B=38°,点D是边AB上一点,点B关于直线CD的对称点为B',当B'D∥AC时,则∠BCD的度数为 .
33°
26.如图,在Rt△ABC中,∠C=90°,∠A=30°,线段AB的垂直平分线分别交AC,AB于点D,E,连接BD.若CD=1,则AD的长为 .
2
解:∵DE垂直平分AB,
∴AE=BE,
∴∠EAB=∠B,
∵∠CAE=∠EAB,
∴∠CAB=2∠B,
∵∠C=90°,∴∠CAB+∠B=90°,
∴∠B=30°.
27.如图,∠ACB=90°,DE垂直平分AB,
∠CAE=∠EAB,求∠B的度数.
28.(补图题)如图,在Rt△ABC中,
∠A=90°,作BC的垂直平分线交AC于点D,延长AC至点E,使CE=AB.若AE=1,求△ABD的周长.
解:如图,连接BD,
∴BD=CD,
∴C△ABD=AB+AD+BD=AB+AD+DC=AB+AC,
∵AB=CE,∴C△ABD=CE+AC=AE=1,
故△ABD的周长为1.
答案图
★29.如图,△DEF为等边三角形,∠1=∠2=∠3.
(1)△ABC是等边三角形吗 为什么
(2)求证:AE+DF=BE.
(1)解:△ABC是等边三角形.理由如下:
∵△DEF是等边三角形,
∴∠DEF=60°,
∴∠AEB=120°,∠1+∠ABE=60° .
∵∠1=∠2,∴∠2+∠ABE=60°,
∴∠ABC=60°.
同理∠ACB=∠BAC=60°,
∴△ABC是等边三角形.
(2)证明:由(1)可得∠AEB=∠CDA=120°,AB=CA,又∵∠1=∠3,∴△ABE≌△CAD(AAS),∴BE=AD,
∵DF=ED,∴AE+DF=AE+ED=AD=BE.
谢 谢
第十三章 轴对称
《轴对称》单元复习
知识点一:轴对称及轴对称图形的相关知识
(1)一个图形沿着一条直线折叠,如果直线两旁的部分能够
,那么这个图形就叫做轴对称图形.这条直线叫做 .
(2)把一个图形沿着某一条直线折叠,如果它能与另一个图形完全 ,那么就说这两个图形关于这条直线(成轴)对称.这条直线叫做 .折叠后重合的点是对应点,叫做 .
对称点
对称轴
重合
对称轴
互相重合
(3)如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的 .
(4)在平面直角坐标系中,关于x轴对称的点的横坐标
,纵坐标 ;关于y轴对称的点的横坐标 ,纵坐标 .
(5)方法指引:注意轴对称图形和轴对称的区别与联系.轴对称图形的对称轴,是任何一对对应点所连线段的
.
垂直平分线
相等
互为相反数
互为相反数
相等
垂直平分线
A B C D
1.(跨学科融合、传统文化)(2022北京一模)2022年北京和张家口成功举办了第24届冬奥会和冬残奥会.下面关于奥运会的剪纸图片中是轴对称图形的是( )
D
2.如图,∠A=30°,∠C'=60°,△ABC与△A'B'C'关于直线l对称,则∠B的度数为( )
A.30° B.60°
C.90° D.120°
C
3.如图,点P为∠AOB内部的点,点P关于OA,OB的对称点P1,P2的连线交OA,OB于M,N两点,连接PM,PN,若P1P2=2,则△PMN的周长为 .
2
4.点A(4,1)关于x轴的对称点B的坐标是 .
5.若点A关于y轴对称的点是(2,3),则点A的坐标为
.
(-2,3)
(4,-1)
知识点二:垂直平分线的性质及判定
(1)定义:经过线段的 且与线段 的直线,叫做线段的垂直平分线.
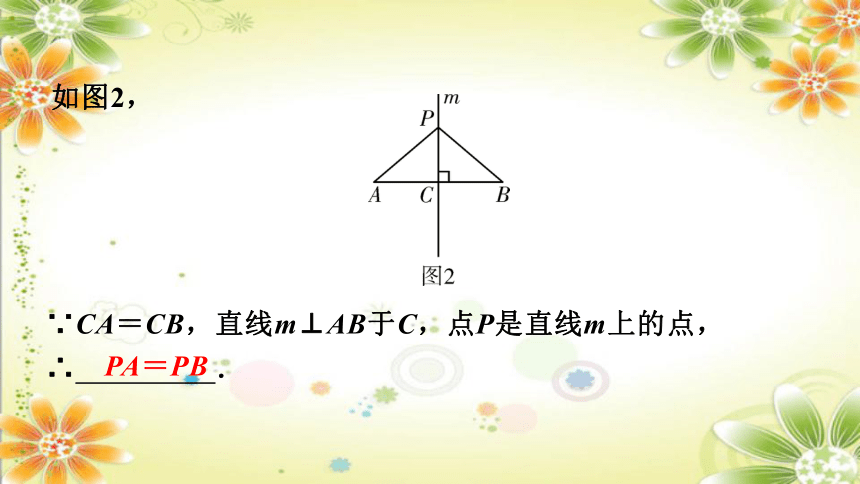
如图1,∵ ,
∴直线m是线段AB的垂直平分线.
(2)性质:线段垂直平分线上的点与线段
两个端点的距离 .
相等
CA=CB,直线m⊥AB于C
垂直
中点
∵CA=CB,直线m⊥AB于C,点P是直线m上的点,
∴ .
如图2,
PA=PB
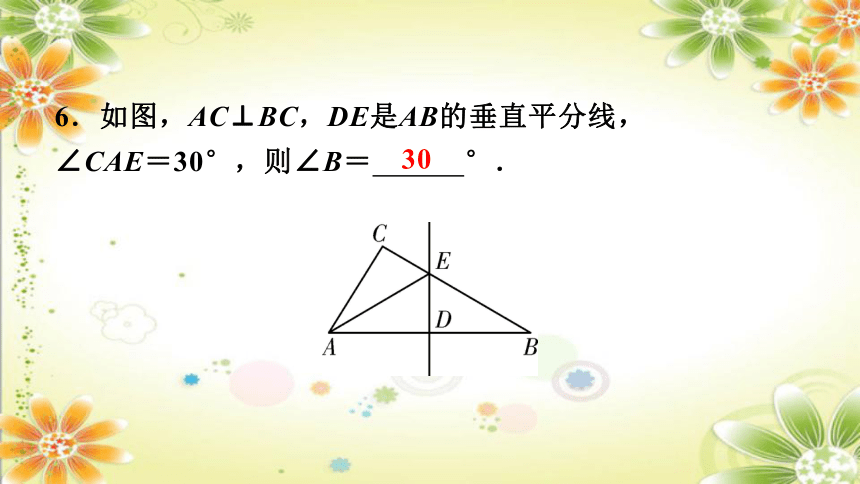
6.如图,AC⊥BC,DE是AB的垂直平分线,
∠CAE=30°,则∠B= °.
30
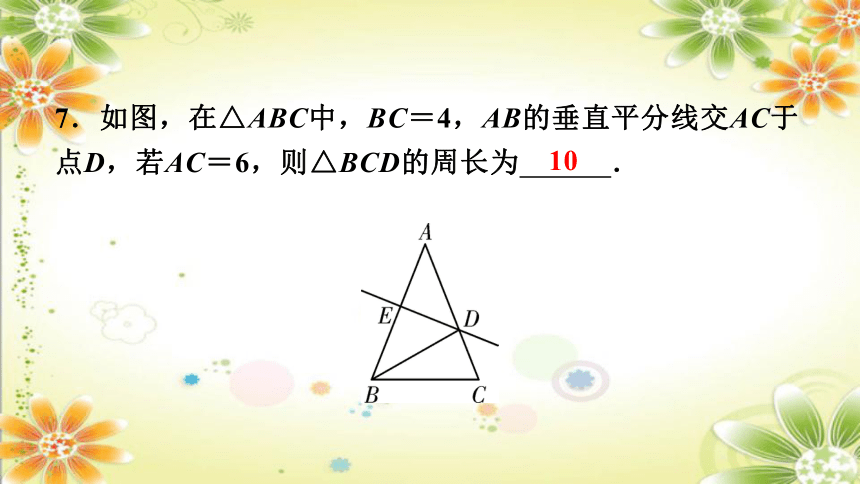
7.如图,在△ABC中,BC=4,AB的垂直平分线交AC于点D,若AC=6,则△BCD的周长为 .
10
∵PA=PB,
直线m是线段AB的垂直平分线,
∴ .
(3)判定:与线段两个端点距离相等的点在线段的
上.
如图3,
点P在直线m上
垂直平分线
8.(全国视野)(2022吉林模拟)如图,在△ABC中,AB的垂直平分线l1交AB于点M,交BC于点D,AC的垂直平分线l2交AC于点N,交BC于点E,l1与l2相交于点O,△ADE的周长为10.
(1)BC的长为 ;
(2)试判断点O是否在边BC的垂直平分线上,并说明理由.
10
解:(2)点O在边BC的垂直平分线上,理由:
连接AO,BO,CO,
∵l1与l2分别是AB,AC的垂直平分线,
∴AO=BO,CO=AO,∴OB=OC,
∴点O在边BC的垂直平分线上.
知识点三:等腰三角形的性质及判定
等腰三角形的性质
(1)等腰三角形的两个底角 .
(简写成“ ”)
(2)等腰三角形的顶角平分线、底边上的 、底边上的 互相重合.(简写成“ ”)
三线合一
高
中线
等边对等角
相等
等腰三角形的判定
(3)定义:有两边 的三角形叫做等腰三角形.
(4)判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也 .(简写成“ ”)
等角对等边
相等
相等
等边三角形的性质
(5)等边三角形是 的特殊的等腰三角形.
(6)等边三角形的三个内角都 ,并且每一个内角都等于 .
60°
相等
三边都相等
等边三角形的判定
(7)由等边三角形的定义判定:三边都 的三角形是等边三角形.
(8)三个角都 的三角形是等边三角形.
(9)有一个角是 的等腰三角形是等边三角形.
60°
相等
相等
含30°角的直角三角形的性质
(10)在直角三角形中,30°角所对的直角边等于
.
斜边的一半
9.如图,在△ABC中,AC=AD=BD,∠B=28°,则∠CAD的度数为 .
68°
10.如图,在△ABC中,∠B=90°,∠BAC=60°,
AB=1,D是BC边延长线上的一点,且∠D=15°,则CD的长为 .
2
11.如图,已知AB∥CD,AC平分∠DAB.求证:△ADC是等腰三角形.
证明:∵AB∥CD,
∴∠BAC=∠DCA,
∵AC平分∠DAB,
∴∠BAC=∠DAC,
∴∠DAC=∠DCA,
∴AD=CD,∴△ADC是等腰三角形.
A B C D
12.【例1】(跨学科融合)(2023鄂州)“国士无双”是人民对“杂交水稻之父”袁隆平院士的赞誉.下列四个汉字中是轴对称图形的是( )
B
小结:利用角平分线、垂直平分线和直角三角形的性质求解.
13.【例2】如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E.若BC=3,则DE的长为( )
A.1 B.2
C.3 D.4
A
小结:关于y轴对称的点的坐标特征是纵坐标相同,横坐标相反.
14.【例3】若点M(a,-3)与点N(1,b)关于y轴对称,则a= ,b= .
-3
-1
小结:求出各个角的度数可得答案.
A.3个
B.4个
C.5个
D.6个
15.【例4】如图,在△ABC中,AB=AC,D,E是BC上两点,∠BAD=∠DAE=∠EAC=36°,则等腰三角形有( )
D
小结:利用等边对等角得到角相等,再利用等角对等边得到答案.
16.【例5】如图,在△ABC中,AB=AC,点E在CA的延长线上,EP⊥BC于点P,交AB于点F,若AF=2,BF=3,则CE的长度为 .
7
小结:充分运用30°角所对直角边等于斜边的一半求解.
A.2 B.4
C.6 D.8
17.【例6】(2022中山一模)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD是斜边AB上的高,
BD=2,则AD的长为( )
C
18.【例7】如图,在△ABC中,AC=4,BC=8,AB的垂直平分线交BC于点D,点E是垂足,求△ACD的周长.
解:∵AB的垂直平分线交BC于点D,∴DA=DB,
∵△ACD的周长=DA+DC+AC,
∴△ACD的周长=DB+DC+AC=BC+AC,
而AC=4,BC=8,∴△ACD的周长=8+4=12.
小结:运用线段垂直平分线的性质定理求解.
19.【例8】(全国视野)(2023淄博)如图,在△ABC中,∠ABC的平分线交AC于点D,过点D作DE∥BC交AB于点E.
(1)求证:BE=DE;
(2)若∠A=80°,∠C=40°,求∠BDE的度数.
(1)证明:∵在△ABC中,∠ABC的平分线交AC于点D,
∴∠ABD=∠CBD,
∵DE∥BC,∴∠EDB=∠CBD,
∴∠EBD=∠EDB,∴BE=DE.
(2)解:∵∠A=80°,∠C=40°,∴∠ABC=60°,
∵∠ABC的平分线交AC于点D,
∴∠ABD=∠CBD=∠ABC=30°,
由(1)知∠EDB=∠EBD,故∠BDE的度数为30°.
小结:角的平分线和平行线结合可得等腰三角形.
A B C D
21.(跨学科融合)(2022金华模拟)自新冠肺炎疫情发生以来,全国人民共同抗疫,某中学积极普及科学防控知识,下面是科学防控知识的图片,其中是轴对称图形的是( )
B
22.(创新题)如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,交AB于点D,若△BCE的周长为8,且AC-BC=2,则AB= .
5
23.已知点A(m-1,3)与点
B(2,n+1)关于x轴对称,则m+n的值为 .
-1
A.①③④ B.①②③④ C.①②④ D.①③
① ② ③ ④
24.如图,在三角形中,AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( )
A
25.(创新题)(2023广州)如图,在△ABC中,AC=BC,∠B=38°,点D是边AB上一点,点B关于直线CD的对称点为B',当B'D∥AC时,则∠BCD的度数为 .
33°
26.如图,在Rt△ABC中,∠C=90°,∠A=30°,线段AB的垂直平分线分别交AC,AB于点D,E,连接BD.若CD=1,则AD的长为 .
2
解:∵DE垂直平分AB,
∴AE=BE,
∴∠EAB=∠B,
∵∠CAE=∠EAB,
∴∠CAB=2∠B,
∵∠C=90°,∴∠CAB+∠B=90°,
∴∠B=30°.
27.如图,∠ACB=90°,DE垂直平分AB,
∠CAE=∠EAB,求∠B的度数.
28.(补图题)如图,在Rt△ABC中,
∠A=90°,作BC的垂直平分线交AC于点D,延长AC至点E,使CE=AB.若AE=1,求△ABD的周长.
解:如图,连接BD,
∴BD=CD,
∴C△ABD=AB+AD+BD=AB+AD+DC=AB+AC,
∵AB=CE,∴C△ABD=CE+AC=AE=1,
故△ABD的周长为1.
答案图
★29.如图,△DEF为等边三角形,∠1=∠2=∠3.
(1)△ABC是等边三角形吗 为什么
(2)求证:AE+DF=BE.
(1)解:△ABC是等边三角形.理由如下:
∵△DEF是等边三角形,
∴∠DEF=60°,
∴∠AEB=120°,∠1+∠ABE=60° .
∵∠1=∠2,∴∠2+∠ABE=60°,
∴∠ABC=60°.
同理∠ACB=∠BAC=60°,
∴△ABC是等边三角形.
(2)证明:由(1)可得∠AEB=∠CDA=120°,AB=CA,又∵∠1=∠3,∴△ABE≌△CAD(AAS),∴BE=AD,
∵DF=ED,∴AE+DF=AE+ED=AD=BE.
谢 谢
