2023-2024学年人教版八年级数学上册13.4最短路径问题课件 24张PPT
文档属性
| 名称 | 2023-2024学年人教版八年级数学上册13.4最短路径问题课件 24张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 479.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-23 06:54:41 | ||
图片预览








文档简介
(共24张PPT)
第十三章轴对称
最短路径问题
教学目标:
【知识与技能】
通过对最短路径问题的探索,进一步理解和掌握“两点之间,线段最短”和“垂线段最短”的性质.
【过程与方法】
经历实践活动的过程,得出最短路径问题的解决方法,找到关于线的对称点实行“折”转“直”,再利用“两点之间,线段最短”这一性质来解决一些简单的实际问题.
【情感态度与价值观】
通过观察、归纳、推理得出数学猜想,让学生体验充满探索性和创造性的数学.
教学重难点:
1运用所学知识解决最短路径问题.
2选择合理的方法解决问题.
1.探索、发现运用轴对称的性质求直线同侧和异侧的两点与直线上一点所连线段的和最小的问题.
2.体验数学活动中的探索与创新,感受数学的严谨性.
知识点一:直线异侧的两点与直线上一点所连线段的和最小的问题
异侧最值方法:利用两点之间线段最短,直接连接找到交点可以得到答案.
1.(人教8上P85)尺规作图:如图,已知直线l及其两侧两点A,B.
(1)在直线l上求一点Q,使到A,B两点距离之和最短;
(2)在直线l上求一点P,使PA=PB.
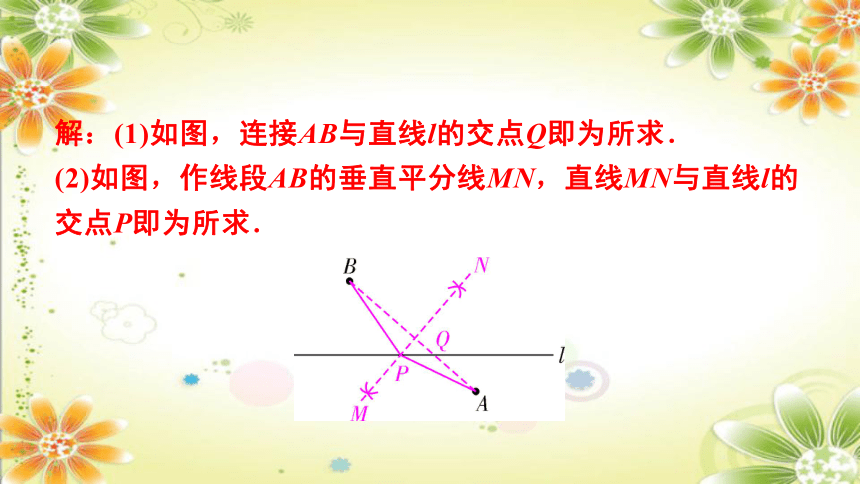
解:(1)如图,连接AB与直线l的交点Q即为所求.
(2)如图,作线段AB的垂直平分线MN,直线MN与直线l的交点P即为所求.
知识点二:直线同侧的两点与直线上一点所连线段的和最小的问题
同侧最值方法:先作其中一点关于直线的对称点,再连对称点与另一点,与直线的交点可以得到答案.
2.(人教8上P85、北师7下P123)如图,A,B是直线l同侧的两点.请在直线l上找一点C,使得AC+CB最小,并说明理由.
解:如图,点C即为所求.
理由:在l上任取一点C',可得AC' +B' C' >AB' ,
即AC' +BC' >AC+BC,∴点C即为所求.
知识点三:最短路径问题的综合运用
综合运用线段垂直平分线的性质定理和两点之间线段最短等知识解决问题.
A.4 B.5 C.6 D.7
3.如图,点P为∠AOB内一点,分别作点P关于OA,OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,若P1P2=6,则△PMN的周长为( )
C
A B C D
4.【例1】(跨学科融合)如图,直线l是一条河,P,Q两地在直线l的同侧,欲在l上的某点M处修建一个水泵站,分别向P,Q两地供水.现有如下四种铺设方案,则铺设的管道最短的方案是( )
B
小结:此类求最短方案问题实质上是两点同侧最小值作法的问题.
5.【例2】(跨学科融合)如图,小河边有两个村庄A,B,要在河边建一自来水厂向A村与B村供水.
(1)若要使厂部到A,B两村的距离相等,则应选择在哪建厂 请在图1中画出点P;
(2)若要使厂部到A,B两村的水管最短,应建在什么地方 请在图2中画出点P.
小结:距离相等(作垂直平分线)和距离最短(作对称)的区别.
图1 图2
图1 图2
解:(1)如图1,点P即为所求.
(2)如图2,点P即为所求.
6.【例3】如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1(要求A与A1,B与B1,C与C1相对应);
(2)在直线l上找一点P,使得PA+PB的和最小.
小结:在网格中最短距离的作法,关键还是找出对称点.
解:(1)如图,△A1B1C1即为所求的三角形.
(2)如图,连接A1B,与直线l交于点P,则点P即为所求.
7.如图均是4×4的正方形网格,已知格点A,格点B和直线l的位置,点P在直线l上.
(1)请分别在图1和图2中作出点P,使PA+PB最短;
(2)请分别在图3和图4中作出点P,使PA-PB最长.
图1 图2 图3 图4
解:(1)如图. (2)如图.
A.4
B.6
C.2
D.3
★8.(2022昆明模拟)如图,在等边△ABC中,AD是BC边上的高,若AD=4,点M,P分别是线段AB,AD上的动点,则MP+BP的最小值为( )
A
解:(2)作A关于y轴的对称点A',
连接A'B,与y轴的交点即为点P,图略.
★9.如图,△ABC的三个顶点的坐标分别是A(-2,3),B(-3,1),C(1,-2).
(1)直接写出点A,B,C关于x轴对称的点A',B',C'的坐标:A'( , ),B’( , ),C'( , );
(2)在y轴上求作一点P,使PA+PB最短.
2
1
-1
-3
-3
-2
课堂小结:
解决最短路径问题,常用的方法是借助轴对称的知识转化,利用“两点之间,线段最短”来求线段和的最小值.
谢谢大家
第十三章轴对称
最短路径问题
教学目标:
【知识与技能】
通过对最短路径问题的探索,进一步理解和掌握“两点之间,线段最短”和“垂线段最短”的性质.
【过程与方法】
经历实践活动的过程,得出最短路径问题的解决方法,找到关于线的对称点实行“折”转“直”,再利用“两点之间,线段最短”这一性质来解决一些简单的实际问题.
【情感态度与价值观】
通过观察、归纳、推理得出数学猜想,让学生体验充满探索性和创造性的数学.
教学重难点:
1运用所学知识解决最短路径问题.
2选择合理的方法解决问题.
1.探索、发现运用轴对称的性质求直线同侧和异侧的两点与直线上一点所连线段的和最小的问题.
2.体验数学活动中的探索与创新,感受数学的严谨性.
知识点一:直线异侧的两点与直线上一点所连线段的和最小的问题
异侧最值方法:利用两点之间线段最短,直接连接找到交点可以得到答案.
1.(人教8上P85)尺规作图:如图,已知直线l及其两侧两点A,B.
(1)在直线l上求一点Q,使到A,B两点距离之和最短;
(2)在直线l上求一点P,使PA=PB.
解:(1)如图,连接AB与直线l的交点Q即为所求.
(2)如图,作线段AB的垂直平分线MN,直线MN与直线l的交点P即为所求.
知识点二:直线同侧的两点与直线上一点所连线段的和最小的问题
同侧最值方法:先作其中一点关于直线的对称点,再连对称点与另一点,与直线的交点可以得到答案.
2.(人教8上P85、北师7下P123)如图,A,B是直线l同侧的两点.请在直线l上找一点C,使得AC+CB最小,并说明理由.
解:如图,点C即为所求.
理由:在l上任取一点C',可得AC' +B' C' >AB' ,
即AC' +BC' >AC+BC,∴点C即为所求.
知识点三:最短路径问题的综合运用
综合运用线段垂直平分线的性质定理和两点之间线段最短等知识解决问题.
A.4 B.5 C.6 D.7
3.如图,点P为∠AOB内一点,分别作点P关于OA,OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,若P1P2=6,则△PMN的周长为( )
C
A B C D
4.【例1】(跨学科融合)如图,直线l是一条河,P,Q两地在直线l的同侧,欲在l上的某点M处修建一个水泵站,分别向P,Q两地供水.现有如下四种铺设方案,则铺设的管道最短的方案是( )
B
小结:此类求最短方案问题实质上是两点同侧最小值作法的问题.
5.【例2】(跨学科融合)如图,小河边有两个村庄A,B,要在河边建一自来水厂向A村与B村供水.
(1)若要使厂部到A,B两村的距离相等,则应选择在哪建厂 请在图1中画出点P;
(2)若要使厂部到A,B两村的水管最短,应建在什么地方 请在图2中画出点P.
小结:距离相等(作垂直平分线)和距离最短(作对称)的区别.
图1 图2
图1 图2
解:(1)如图1,点P即为所求.
(2)如图2,点P即为所求.
6.【例3】如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1(要求A与A1,B与B1,C与C1相对应);
(2)在直线l上找一点P,使得PA+PB的和最小.
小结:在网格中最短距离的作法,关键还是找出对称点.
解:(1)如图,△A1B1C1即为所求的三角形.
(2)如图,连接A1B,与直线l交于点P,则点P即为所求.
7.如图均是4×4的正方形网格,已知格点A,格点B和直线l的位置,点P在直线l上.
(1)请分别在图1和图2中作出点P,使PA+PB最短;
(2)请分别在图3和图4中作出点P,使PA-PB最长.
图1 图2 图3 图4
解:(1)如图. (2)如图.
A.4
B.6
C.2
D.3
★8.(2022昆明模拟)如图,在等边△ABC中,AD是BC边上的高,若AD=4,点M,P分别是线段AB,AD上的动点,则MP+BP的最小值为( )
A
解:(2)作A关于y轴的对称点A',
连接A'B,与y轴的交点即为点P,图略.
★9.如图,△ABC的三个顶点的坐标分别是A(-2,3),B(-3,1),C(1,-2).
(1)直接写出点A,B,C关于x轴对称的点A',B',C'的坐标:A'( , ),B’( , ),C'( , );
(2)在y轴上求作一点P,使PA+PB最短.
2
1
-1
-3
-3
-2
课堂小结:
解决最短路径问题,常用的方法是借助轴对称的知识转化,利用“两点之间,线段最短”来求线段和的最小值.
谢谢大家
